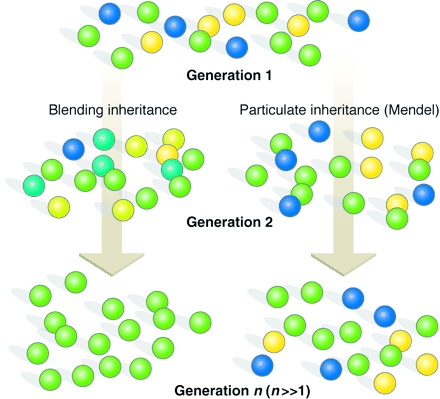
 Darwin una vez escribió «siento muchísimo no haber profundizado lo suficiente para comprender los grandes principios que guían la matemática; ya que los que los dominan parecen dotados de un sentido extra.» Como nos recuerda Robert M. May, en «Uses and Abuses of Mathematics in Biology,» Science, 303: 790-793, 2004 . Una de las críticas más importantes a Darwin, por parte del ingeniero Fleeming Jenkin y otros, fue que la herencia que mezcla características del padre y de la madre no puede preservar la variación natural («blending inheritance» en la figura). Las observaciones de Mendel, contemporáneas a Darwin, resolvían este dilema, como mostraron Fisher y otros, pero fue necesario medio siglo hasta que Hardy y Weinberg resolvieran matemáticamente este problema gracias a su demostración de 1908 de que la herencia (Mendeliana) preserva la variación en las poblaciones. El teorema o la ley de Hardy-Weinberg equivalen a la Primera Ley de Newton (los cuerpos en reposo o en movimiento uniforme en línea recta, mantienen este estado si no se aplican fuerzas externas): la frecuencia de los genes en una población no se altera de generación en generación si están ausentes fenómenos poblacionales externos, como la migración, selección, fluctuaciones estadísticas, o mutaciones. La entrada de la wiki es muy clara y recomiendo su lectura a los interesados.
Darwin una vez escribió «siento muchísimo no haber profundizado lo suficiente para comprender los grandes principios que guían la matemática; ya que los que los dominan parecen dotados de un sentido extra.» Como nos recuerda Robert M. May, en «Uses and Abuses of Mathematics in Biology,» Science, 303: 790-793, 2004 . Una de las críticas más importantes a Darwin, por parte del ingeniero Fleeming Jenkin y otros, fue que la herencia que mezcla características del padre y de la madre no puede preservar la variación natural («blending inheritance» en la figura). Las observaciones de Mendel, contemporáneas a Darwin, resolvían este dilema, como mostraron Fisher y otros, pero fue necesario medio siglo hasta que Hardy y Weinberg resolvieran matemáticamente este problema gracias a su demostración de 1908 de que la herencia (Mendeliana) preserva la variación en las poblaciones. El teorema o la ley de Hardy-Weinberg equivalen a la Primera Ley de Newton (los cuerpos en reposo o en movimiento uniforme en línea recta, mantienen este estado si no se aplican fuerzas externas): la frecuencia de los genes en una población no se altera de generación en generación si están ausentes fenómenos poblacionales externos, como la migración, selección, fluctuaciones estadísticas, o mutaciones. La entrada de la wiki es muy clara y recomiendo su lectura a los interesados.
El artículo de May nos presenta varios ejemplos en los que «biólogos» abusan del uso de modelos estadísticos en los que se «asumen» ciertas hipótesis «no probadas» para obtener conclusiones, algunas intuitivamente absurdas. Recomiendo su lectura. May nos recuerda que hasta hace pocas décadas quienes aplicaban la matemática y la estadística en biología poseían una formación sólida en matemáticas, pero que en la actualidad, como está tan de moda la llamada «biología de sistemas» (nuevo nombre para la «biología matemática» de siempre) muchos usan estas técnicas para obtener conclusiones (fenómenos emergentes), supuestamente ratificadas por el modelo matemático, sin un conocimiento claro de lo que están haciendo y de las hipótesis necesarias para sustentarlos. Según May, esto es preocupante. Por ejemplo, muchos presuponen que cualquier perturbación estadística sigue una distribución gaussiana, incluso cuando el fenómeno es fuertemente no lineal, olvidando que en dinámica de sistemas no lineales los «sucesos raros» son mucho más importantes de lo que una distribución gaussiana presupone. Más aún, May nos indica que muchos de los abusos que actualmente está observando no son siempre fáciles de reconocer, incluso para los matemáticos, no digamos para los «pobres biólogos».
Y todo esto me ha venido a la mente tras releer «Pruebas y refutaciones,» de Imre Lakatos, oportunamente recomendada por JL Pérez de la Cruz. Gracias, compañero.


Muy muy interesante. Desde luego es entrar a tu blog, leer, y culturizarme.
Gracias como siempre por abrirme las fronteras de la curiosidad
Un saludo!