 En 2005, los franceses Couder, Protière, Fort y Badouad mostraron que gotitas de aceite rebotando en una bandeja de aceite en vibración mostraban un comportamiento similar a la teoría de la onda piloto (o interpretación causal de la mecánica cuántica) de Louis de Broglie (1927) y David Bohm (1952), una formulación de la mecánica cuántica equivalente a la convencional. Este sistema clásico permite simular los experimentos de doble rendija, el efecto túnel, presentan niveles de energía cuantizados y muestran el fenómeno de creación/destrucción de pares partícula/antipartícula. ¿Por qué ocurre esta analogía? Nos lo explican Robert Brady, Ross Anderson, «Why bouncing droplets are a pretty good model of quantum mechanics,» arXiv:1401.4356 [quant-ph], 16 Jan 2014.
En 2005, los franceses Couder, Protière, Fort y Badouad mostraron que gotitas de aceite rebotando en una bandeja de aceite en vibración mostraban un comportamiento similar a la teoría de la onda piloto (o interpretación causal de la mecánica cuántica) de Louis de Broglie (1927) y David Bohm (1952), una formulación de la mecánica cuántica equivalente a la convencional. Este sistema clásico permite simular los experimentos de doble rendija, el efecto túnel, presentan niveles de energía cuantizados y muestran el fenómeno de creación/destrucción de pares partícula/antipartícula. ¿Por qué ocurre esta analogía? Nos lo explican Robert Brady, Ross Anderson, «Why bouncing droplets are a pretty good model of quantum mechanics,» arXiv:1401.4356 [quant-ph], 16 Jan 2014.
El rebote de las gotitas en la superficie ondulante está regido por una ecuación de ondas que es análoga a la ecuación de Schrödinger, donde la constante de Planck se sustituye por una constante asociada al movimiento. La velocidad de las ondas en la superficie del aceite (que depende de la frecuencia de vibración) se comporta como la velocidad de luz en la teoría de la relatividad, es decir, como una velocidad máxima inalcanzable, con lo que esta ecuación de ondas es covariante Lorentz.
Las gotas rebotan como si estuvieran en un campo magnético generado por una fuerza radial que depende del inverso de la distancia al cuadrado (esta fuerza es atractiva o repulsiva según la fase relativa entre la oscilación de las gotas saltarinas y la de las ondas de la superficie). Además, esta fuerza hace que una pareja de gotas se describa por una función antisimétrica, es decir, se comporta como si cada gota tuviera un espín semientero (como el electrón) y se cumpliera el principio de exclusión de Pauli.
Por supuesto, también hay diferencias entre el comportamiento clásico de las gotas y las predicciones de la mecánica cuántica (o de la teoría de la onda piloto). Por ello no hay que abusar de esta analogía clásica y no se debe afirmar que es un análogo a una teoría de variables ocultas. A todos los interesados en la interpretación de la mecánica cuántica les recomiendo leer el artículo de Brady y Anderson, que aclara este punto en detalle. Permíteme un breve resumen.
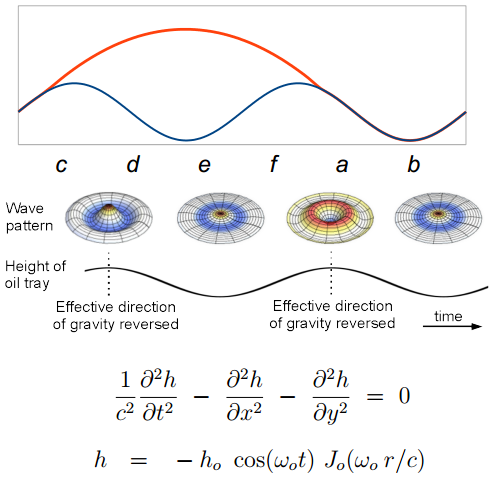 El rebote de una gota (curva roja) sobre la oscilación de la superficie (curva azul) se basa en el llamado refuerzo paramétrico (parametric reinforcement). Las ondas de la superficie del aceite se describen por una ecuación de ondas invariante Lorentz para la altura del fluido (h) respecto a la superficie en reposo, cuya solución en coordenadas cilíndricas depende en la dirección radial de la función de Bessel J0(r/c).
El rebote de una gota (curva roja) sobre la oscilación de la superficie (curva azul) se basa en el llamado refuerzo paramétrico (parametric reinforcement). Las ondas de la superficie del aceite se describen por una ecuación de ondas invariante Lorentz para la altura del fluido (h) respecto a la superficie en reposo, cuya solución en coordenadas cilíndricas depende en la dirección radial de la función de Bessel J0(r/c).
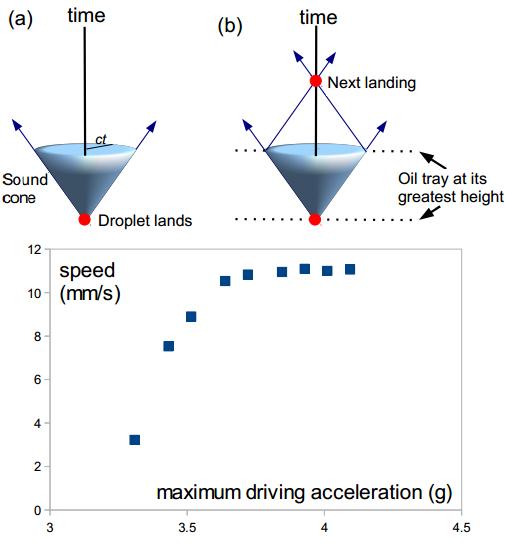
La invarianza Lorentz permite entender el refuerzo paramétrico utilizando «conos sónicos» (análogos a los conos de luz en relatividad), es decir, mediante una reflexión de Bragg. La velocidad de las gotas en horizontal en función de la aceleración que reciben en las colisiones con la superficie sigue una curva análoga a la velocidad de un partícula relativista en función de su energía cinética. La gran diferencia es que la velocidad máxima depende de la frecuencia de la oscilación de la superficie (lo que equivaldría a que la velocidad de la luz fuera variable).
En esta figura se ve una gota que se mueve hacia la derecha. A baja velocidad (a) se encuentra casi en el centro de la oscilación de la superficie. Sin embargo, a mayor velocidad (b) y (c) la onda se deforma mostrando una estela tras la gota en forma de cono, resultado de la simetría Lorentz «efectiva» de este sistema.
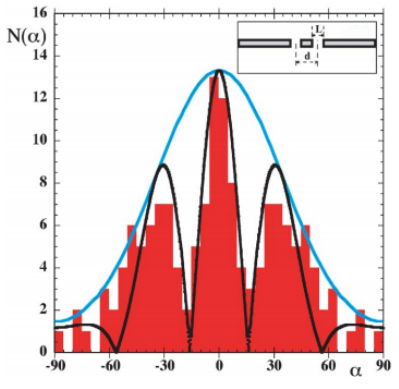
La teoría clásica de la difracción de ondas permite explicar a la perfección el comportamiento aparentemente cuántico de las gotas en un experimento de doble rendija. Brady y Anderson presentan los resultados de simulaciones numéricas que muestran esta analogía.
Este histograma muestra el ángulo de salida de 75 gotas que han pasada por una de las dos rendijas en un experimento de doble rendija. La línea negra muestra el resultado teórico según la teoría de la difracción de ondas (que coincide con lo esperado en mecánica cuántica).
La simetría Lorentz aproximada permitida derivar una ecuación de Klein-Gordon para las gotas que, en el limíte «no relativista» permite obtener la ecuación de Schrödinger de la mecánica cuántica. La constante de Planck efectiva corresponde a la constante que multiplicada por la frecuencia nos da el análogo clásico a la energía en la famosa fórmula de Einstein para la simetría Lorentz aproximada.
Un par de gotas en rotación mutua se comportan como el análogo a un sistema con espín 1/2 (el mismo fenómeno se da en dos péndulos acoplados). La descripción de este sistema se puede hacer en un análogo a la esfera de Bloch para un cubit, lo que permite introducir un álgebra de matrices de Pauli para la descripción de este sistema.
En resumen, por muy sugerente que resulte la analogía, no es más que eso, una analogía. Todas las expresiones «cuánticas» que describen el sistema de gotas danzarinas son aproximadas y tienen un rango de validez limitado. El artículo de Brady y Anderson nos explican en detalle esta analogía, que podría ser útil en la enseñanza de la física (quizás en un primer curso de mecánica cuántica). Esta analogía clásica, aunque sea de validez limitada, pueda ayudar a los estudiantes a superar su perplejidad inicial hacia el concepto de función de onda de la mecánica cuántica. Al fin y al cabo no es más que eso, una onda.




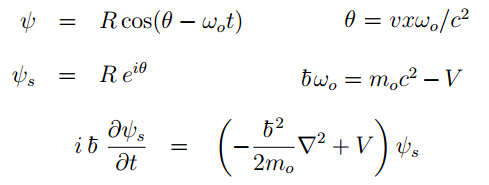

estimado, puede indicarme, si es posible colocar una cantidad medida de aceite lubricante (digamos 2 mililitros) sobre un vaso transparente de agua quieta y colocarlo sobre una plataforma vibratoria con valor conocido de vibraciones ondas frecuencias etc. y ver si la gran gota se rompe en gotas más chicas. Varias veces hasta determinar el valor de vibración en la que no se rompe, de esta manera puedo repetirlo en un sitio de vibraciones desconocidas y obtener un valor por sobre la conocida si se rompe o inferior si no se rompe en microgotas? gracias
Existe una frecuencia de vibración del fluido que permita el surgimiento de gotas de manera espontánea análogo a la aparición de partículas virtuales de un campo cuántico?
No, Vicente, las gotas danzantes simulan la teoría de la onda-piloto que es una teoría cuántica no relativista; las partículas virtuales aparecen en física cuántica relativista. Las partículas virtuales no tienen análogo en los sistemas de gotas danzantes.