El vacío es una substancia que presenta fluctuaciones cuánticas a temperatura cero que se pueden transmitir de un lugar a otro. Se publica en PNAS un artículo titulado «fuerzas de vacío gigantes en líneas de transmisión,» que presenta un modelo teórico de la propagación de «señales vacías» (puras fluctuaciones cuánticas) en una línea coplanar superconductora situada entre dos dipolos. Las fuerzas de vacío de van der Waals (vdW) y de Casimir (Cas) se amplifican tanto en este sistema que los autores hablan de «fuerzas gigantes.» Por cierto, en guías de onda metálicas huecas y en fibra óptica no se puede dar esta amplificación.
Las conclusiones de este curioso artículo teórico deberán ser confirmadas en estudios experimentales. Más información en Ephraim Shahmoon, Igor Mazets, Gershon Kurizki, «Giant vacuum forces via transmission lines,» PNAS, Early Edition, 7 Jul 2014. En la conferencia de la Sociedad de Física de Israel titularon los autores su charla «Transmitting the signal of ‘nothing’: Giant vacuum forces via transmission lines» IPS Conf. 2013 (PPTX slides, ZIP file). Pero yo no me he atrevido a titular esta entrada «La transmisión de ‘nada’ en una línea coplanar eléctrica.»
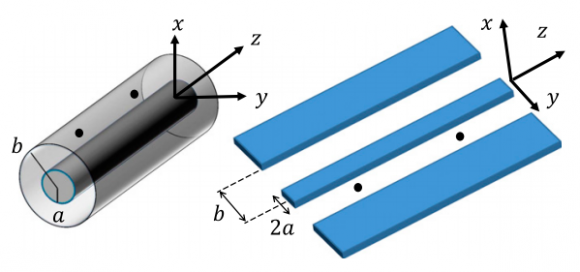
Las fluctuaciones cuánticas del vacío del campo electromagnético inducen fuerzas entre partículas neutras. En una línea de transmisión en la que se puede propagar modos TEM (transversal-electromagnéticos) se amplifica la interacción entre dos dipolos de tal forma que se logran fuerzas de vacío «gigantes» (por supuesto, en los cálculos teóricos se asume que la línea es perfectamente conductora y que se encuentra en el cero absoluto de temperaturas, una aproximación válida para líneas coplanares superconductoras).
Como los cálculos teóricos podrían ser discutibles, los autores se curan en salud y calculan las fuerzas de vacío por dos métodos diferentes que conducen exactamente al mismo resultado. Por un lado, utilizan la teoría de perturbaciones en electrodinámica cuántica (QED). Y por otro lado, la solución de la ecuación de onda electromagnética bajo un campo de vacío, en la llamada teoría de la dispersión (o scattering) de fluctuaciones de vacío. El segundo método es más directo y fácl de ejecutar pero, al estar basado en una aproximación cuasiclásica, los autores han preferido aplicar también el primer método que es puramente cuántico.
Por cierto, ¿qué significa «gigante» en este contexto? Esta figura lo muestra, pero quizás requiere una aclaración. La fuerza atractiva entre los dos dipolos en función de la distancia interdipolar, sea r, resulta ser para r pequeño (a distancias cortas) igual a const.+(r/λ) ln(r/λ), donde λ es la longitud de onda dipolar típica, y para r grande (a distancias grandes) igual a 1/r3. ¿Gigantes? Por supuesto, estas expresiones son gigantes comparadas con las que se obtienen en el espacio vacío (sin línea de transmisión) que para r pequeño son igual a 1/r^6 y para r grande igual a 1/r7. Estos resultados son válidos tanto para las fuerzas de van der Waals como para las de Casimir.
No quiero entrar en los detalles técnicos (que a mí me convencen, pero ya sabéis que yo no soy experto en estas lides). De hecho, uno de los motivos para escribir esta entrada es aprovechar que entre los lectores habituales de este blog se encuentran algunos expertos en el cálculo de fuerzas de Casimir para pedirles por favor que nos aclaren si los cálculos del artículo de PNAS les convencen. No pido más (aunque sé que no es poco).
Por supuesto, como en todos los artículos teóricos sobre un fenómeno nunca observado y altamente exótico, hay que tener los pies en la tierra y ser muy cautos. La demostración experimental de estas fuerzas de vacío gigantes puede tardar lustros y podría haber fenómenos no considerados en el modelo teórico que minimizan el efecto de la amplificación destruyendo la coletilla de «gigantes» (que es necesaria para la verificación experimental de un fenómeno tan sutil en su defecto). Habrá que estar al tanto sobre lo que opinan los expertos en fuerzas de Casimir sobre este nuevo y muy sugerente trabajo.
PS 02 Ago 2014: Recomiendo leer a Steve K. Lamoreaux, «Casimir forces: Still surprising after 60 years,» Physics Today, Feb 2007; Johanna Miller, «Casimir forces between solids can be repulsive,» Physics Today, Feb 2009; y Richard J. Fitzgerald, «The Casimir force in one dimension,» Physics Today, Ago 2014.




No se puede acceder al artículo (sin la subscripción pertinente), así que creo que la pregunta es obligada: ¿en magnitud, «gigante», de cuánto estamos hablando? Entiendo que se refieren a «gigantes» para la escala que estamos hablando, ¿o se refieren realmente a intensidades «macroscópicas»?
Gracias, AaRIW, buena pregunta. La verdad es que la esperaba pues se me olvidó aclararla. He añadido una explicación en la propia entrada.
Hola Francis,
Yo trabajo en efecto Casimir y estoy familiarizado con este tipo de cálculos teóricos, y te puedo decir que a mí sus cálculos teóricos me convencen.
El incremento de la fuerza de Casimir se da porque la relación de dispersión del modo TEM de propagación es 1D, en vez de 3D como en el caso de los modos TE y TM, por lo que en principio, siempre que tengas una fibra con modos TEM, aparecerá esta fuerza de Casimir «extra» (con las debidas correcciones cuando el sistema no es tan ideal).
Gracias, Pablo.
Hola Antonio,
En general, las fuerzas de Casimir se pueden interpretar como fuerzas entre polarizabilidades de partículas inducidas por el medio. Cuando la temperatura del medio es el cero absoluto, las únicas fluctuaciones que quedan son las fluctuaciones de punto cero. Esta es la interpretación que podríamos llamar cuántica, y cuando se calculan fuerzas de Casimir usando teoría de perturbaciones de QED, estás asumiendo esta interpretación.
Existe otra interpretación debida a Lifshitz, que propuso que el efecto Casimir surgía de la interacción entre corrientes estocásticas generadas dentro de los cuerpos. En este caso, para hacer cálculos usas el teorema Fluctuación-Disipación y calculas la fuerza usando el tensor energía-impulso o resolviendo la función de partición del problema. Al usar el método de scattering, estás asumiendo esta otra interpretación.
Al final, se puede demostrar que ambas interpretaciones son totalmente equivalentes para el cálculo de fuerzas de Casimir.
La mejor referencia que se me ocurre es la introducción del último libro-review del tema, «Casimir Physics», editado por Springer en 2011, lo puedes encontrar en el enlace adjunto
http://link.springer.com/book/10.1007%2F978-3-642-20288-9
Hola Antonio, el truco, al sumar energías de punto cero, es tener sólo en cuenta la parte de la energía que depende de la distancia entre los objetos y despreciar el resto. Por ello hay que restar a la energía total la energía del sistema cuando los cuerpos se encuentran a una distancia infinita.
Ten en cuenta que así estamos eliminando la parte de la energía en la que no estamos interesados para describir el efecto Casimir, pues es independiente de la distancia.
Por cierto, ¿Qué significa temperatura del Vacío?. Entendía que el el concepto de temperatura es algo aplicable a un sistema de muchas partículas. ¿Pero en el Vacío?. ¿Se puede asignar una temperatura a un sistema de partículas virtuales?. ¿Cual sería la distribución de velocidades?.
Hola,
Siento entrar en este artículo tan tarde, pero me preguntaba si sería posible que alguien explicara alguna aplicación práctica de este fenómeno tan interesante (supongo que en NEMs).
Además ¿Se ha avanzado algo más en este tiempo?
Saludos y gracias