En física clásica, si lanzas una moneda obtienes cara o cruz. En física cuántica, tras una medida el resultado de lanzar una moneda es cara o cruz. Sin embargo, una medida cuántica débil te puede dar un resultado cualesquiera; si asocias uno a cara y cero a cruz, puedes obtener un valor como cien, o como menos tres. ¿Qué significan estos resultados de medidas cuánticas débiles? En ciertos experimentos se descartan las medidas cuánticas débiles que dan valores «fuera de rango» y sólo se obtienen valores uno (cara ), o cero (cruz). ¿Qué implica este proceso de postselección del resultado? ¿Cómo influye en la interpretación del resultado?
Yo no te lo puedo explicar, pues no lo entiendo. Esta entrada está basada en lo que cuenta Adrian Cho, «Breakthrough lost in coin toss?,» Science 346: 22-23, 3 Oct 2014, que comenta el artículo técnico de Christopher Ferrie, Joshua Combes, «How the Result of a Single Coin Toss Can Turn Out to be 100 Heads,» Phys. Rev. Lett. 113: 120404, 18 Sep 2014, arXiv:1403.2362 [quant-ph].
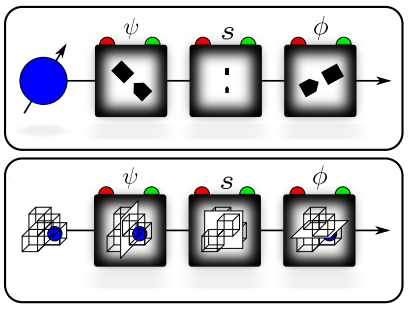
En 1988, Yakir Aharonov (Univ. Chapman, Orange, California) y Lev Vaidman (Univ. Tel Aviv, Israel) introdujeron el concepto de medida cuántica débil mediante la postselección del estado en un experimento tipo Stern-Gerlach doble. El nuevo artículo publicado en Physical Review Letters trata de explicar mediante estadística clásica los resultados de dicho experimento. El artículo de Christopher Ferrie (Univ. Nuevo México, Albuquerque) y Joshua Combes (Instituto Perimeter de Física Teórica, Waterloo, Canadá), propone que la «magia» cuántica no aplica a las medidas débiles.
Obviamente, el artículo ha sido criticado por el propio Aharonov, que afirma sin más detalles que Ferrie y Combes no han entendido lo que son las medidas cuánticas débiles. El modelo clásico de Ferrie y Combes no describe todas las propiedades de las medidas débiles, luego no aporta información sobre ellas. La «magia» cuántica sigue asociada a las medidas débiles.
Los pensamientos de Aharonov han sido verbalizados por Eliahu Cohen, «A comment on «How the result of a single coin toss can turn out to be 100 heads»,» arXiv:1409.8555 [quant-ph], y Aharon Brodutch, «Comment on: How the result of a single coin toss can turn out to be 100 heads (arXiv:1403.2362),» arXiv:1410.8510 [quant-ph].
Por supuesto, Ferrie y Combes han contestado a la recíproca. Quienes no entienden su modelo clásico son Cohen, Brodutch y el propio Aharonov. Nos lo cuentan en su nuevo artículo Christopher Ferrie, Joshua Combes, «Classical correlation alone supplies the anomaly to weak values,» arXiv:1410.8067 [quant-ph].
Igual que ocurre con un partido de tenis entre Rafa Nadal y Novak Djokovic, por mucho que te cuenten lo que ha pasado, para disfrutar del partido tienes que verlo con tus propios ojos. Si te interesa este debate entre Ferrie–Combes y Aharonov–Cohen–Brodutch debes leerlo por ti mismo. Aún así, permíteme un breve resumen.
Los físicos que estudiamos mecánica cuántica aprendemos cómo se realizan las medidas cuánticas de un sistema y cómo se interpretan sus resultados siguiendo las ideas de los padres de esta rama de la física a finales de la década de 1920. Los resultados tienen valores que son números reales y probabilidades bien definidas. El estado de un sistema cuántico se describe como un vector en un espacio de Hilbert (que es un espacio vectorial y tiene infinitas bases de vectores). El aparato de medida, por construcción, tiene asociado un observable, un operador lineal hermítico en el espacio de Hilbert cuyos autovectores son ortogonales y definen una única base; además, los valores del observable (las medidas) corresponden a los autovalores asociados a dichos autovectores.
Antes de la medida, el sistema está en un estado de superposición lineal, un vector en el espacio de Hilbert que se puede describir en la base de autovectores asociada al observable a medir. Los coeficientes en esta base son amplitudes de probabilidad, cuyo cuadrado determina la probabilidad de que el sistema tras la medida se describa con cierto autovector y la medida resulte en un valor igual a su correspondiente autovalor. El aparato de medida (o el observable a medir) determinan la base del espacio a usar antes y después de la medida.
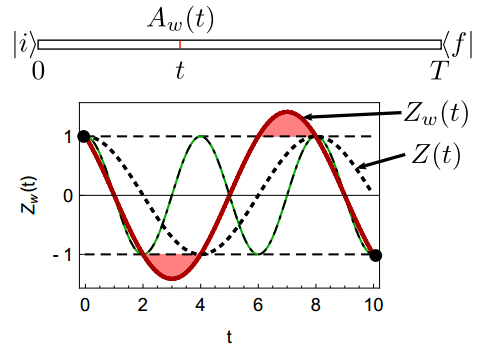
Las medidas cuánticas débiles usan un protocolo completamente diferente, sencillo, pero diferente. Como el espacio de Hilbert tiene infinitas bases, se asume que la base que describe el estado inicial (preselección) y la base que describe el estado final (postselección) son diferentes (por ejemplo, podrían corresponder a dos observables diferentes, incluso complementarios, como la posición y la velocidad). Por tanto, el resultado de la medida no corresponde a un autovalor de la base preseleccionada, sino a una combinación lineal (normalmente infinita) de dichos autovalores. Por tanto, el valor de la medida débil puede ser un número fuera de rango (por ejemplo, una posición compleja imaginaria pura, o una energía negativa); además, su amplitud de probabilidad al cuadrado no resulta en una probabilidad (aparecen «probabilidades» negativas o mayores que la unidad).
Interpretar los resultados de las medidas débiles no es fácil. A veces se realizan «trucos» ad hoc (tomar la parte real de números complejos u omitir los resultados que tienen asociadas probabilidades negativas) para que el resultado de la medida parezca «razonable» (es decir, pueda ser interpretado con facilidad). En ciencia, elegir el resultado que conviene, omitiendo los resultados que no convienen, en otras áreas de la ciencia se llama mala ciencia. Pero como las medidas débiles están de moda, parece que hay muchos físicos a los que no les importa.
Los lectores habituales de este blog saben que detesto no ser capaz de interpretar el resultado de un experimento y tenerme que creer la interpretación que ofrecen los autores del artículo. Por ello me gustó mucho el artículo de Ferrie y Combes cuando lo leí antes del verano. Pero no quiero engañar a nadie, he esperado a que aparecieran múltiples críticas para hacerme una mejor idea del trabajo. Que a mí me convenza no significa que convenza a un experto en medidas cuánticas débiles.
El artículo de Ferrie y Combes trata de explicar usando física clásica los resultados del experimento original de Aharonov–Vaidman. Según algunos físicos, incluso si explica bien dicho experimento (algo que no está del todo claro, según Aharonov), no implica que otros protocolos de medida débil también tengan una explicación clásica. Prescindir de las medidas débiles significa no poder violar el principio de indeterminación de Heisenberg o no poder determinar la función de onda de un sistema cuántico. Mucha «magia» cuántica publicada en los últimos años iría directa a la basura. Por ello no deben extrañar todas las críticas vertidas en los últimos meses.
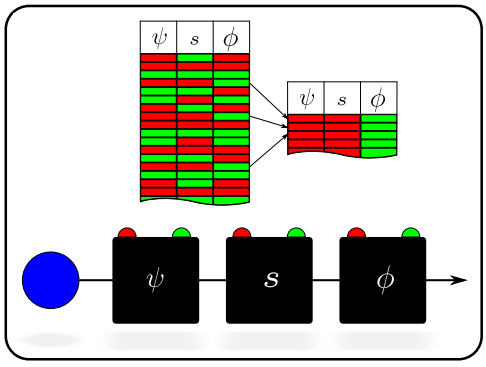
Ferrie y Combes nos proponen un experimento mental entre Alicia y Berto. Alicia lanza una moneda clásica y Berto mide su estado con cierta incertidumbre; por ejemplo, toca la moneda con el dedo pero sin poder verla con los ojos. La medida de Berto puede alterar el estado de la moneda (al tocarla con los dedos, con cierta probabilidad puede darle la vuelta sin darse cuenta). Berto le devuelve la moneda a Alicia y le anuncia el resultado de su medida (cara o cruz). Si el resultado anunciado por Berto es cara, Alicia mira la moneda para confirmarlo o desmentirlo. Si el resultado anunciado por Berto es cruz, Alicia no hace nada. El resultado de la medida débil simulada es el número de veces que Alicia ha encontrado cara (postselección) cuando Berto le dijo que era cara (preselección). Ferrie y Combes argumentan que este experimento clásico reproduce una medida cuántica débil.
Según Aharonov, aunque para ciertas tasas de error en la medida de Berto, el resultado clásico reproduzca el valor de la medida débil, las medidas cuánticas usan física cuántica que el modelo clásico de Ferrie y Combes no tiene en cuenta. Por tanto, aunque las matemáticas coincidan (por ello el artículo se ha publicado en la revista Physical Review Letters), la física es errónea y la coincidencia es puramente casual. Para Aharonov es obvio que el esquema de Ferrie y Combes es clásico y no puede reproducir los resultados cuánticos, aunque sean de medidas débiles.
Varios físicos han tratado de hacer explícito el fenómeno de interferencia cuántica en las medidas débiles con objeto de invalidar el modelo de Ferrie y Combes (que al ser clásico no puede incorporar este fenómeno). Un buen ejemplo es el artículo de Justin Dressel, «Weak Values are Interference Phenomena,» arXiv:1410.0943 [quant-ph]. La interferencia cuántica puede dar lugar a «probabilidades negativas» que no se pueden obtener en ningún modelo clásico de variables ocultas. Su artículo presenta un ejemplo de estas «probabilidades negativas» en el contexto de las medidas débiles. El problema es que, en mi opinión, su artículo no cierra todos los loopholes posibles y parte de sus «probabilidades negativas» de supuesto origen cuántico podrían tener su origen en las «probabilidades negativas anómales» inducidas por la postselección en la medida débil.
He de confesar que en el trabajo de Dressel si me dejo guiar por las operaciones matemáticas, me convence. Pero si me pongo a pensar en el significado de cada una de las fórmulas matemáticas, me quedo a disgusto. Me parece que, como el as que oculta el mago en su manga, hay gato encerrado. Y no es un gato de Schrödinger.
El año 2015 será otro año más en el que debatiré en público en este blog mis dificultades a la hora de entender la interpretación de las medidas cuánticas débiles. La verdad, la mecánica cuántica es muy sencilla de entender, pero muy difícil de interpretar. Las medidas cuánticas débiles son el mejor ejemplo. ¿Lograré interpretarlas a gusto en 2015? Yo no pierdo la esperanza.