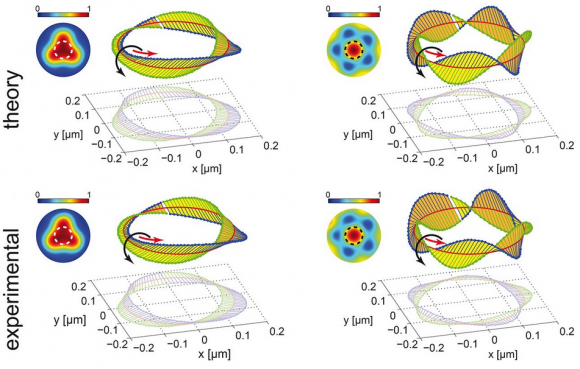
Seguro que has fabricado alguna vez una banda de Moebius con papel. También se puede fabricar con luz gracias a la polarización. Para ello se usa un haz de luz con estructura (un haz de Poincaré) que se obtiene pasando la luz de un láser a través de una lente de cristal líquido especial. Con luz polarizada se han observado bandas de Möbius simples (tres medias vueltas, parte izquierda de la figura) y dobles (cinco medias vueltas, parte derecha).

El artículo técnico es Thomas Bauer et al., «Observation of optical polarization Möbius strips,» Science, 29 Jan 2015; doi: 10.1126/science.1260635. También recomiendo leer a Isaac Freund, «Cones, spirals, and Möbius strips, in elliptically polarized light,» Optics Communications 249: 7-22, 2005; doi: 10.1016/j.optcom.2004.12.052, y Isaac Freund, «Multitwist optical Möbius strips,» Optics Letters 35: 148-150, 2010; doi: 10.1364/OL.35.000148.

El campo electromagnético tiene dos componentes (en ciertos ejes una magnética y una eléctrica). Por tanto, el campo cuántico de un fotón tiene dos componentes que pueden excitarse de forma independiente. Gracias a ello cada fotón tiene un polarización (ambs componentes pueden estar excitadas al unísono). Una onda electromagnética clásica puede tener una polarización bien definida si todos sus fotones la tienen. En física clásica la polarización se describe mediante un vector en un plano cuyas dos componentes oscilan en frecuencia. Si oscilan al unísono hablamos de polarización lineal, si oscilan con un desfase de un cuarto de onda tenemos polarización circular y en cualquier otro caso polarización elíptica (el vector de polarización describe una elipse). En la propagación de un haz de luz en tres dimensiones el plano de esta elipse puede rotar. Gracias a ello la luz puede describir conos, cintas en espiral y cintas de Möbius.

En tres dimensiones la orientación del plano de la elipse de polarización se describe mediante un sistema de tres ejes: los dos ejes de la elipse y el eje perpendicular al plano. A cada eje le podemos asignar tres índices topológicos, con lo que obtenemos 27 configuraciones posibles. Eliminando las tres asociadas a la polarización lineal y las tres asociadas a la polarización circular resultan 21 índices topológicos. Gracias a ello el espacio de posibles orientaciones espaciales de la elipse de polarización se puede dividir en 2^21 = 2 097 152 de regiones diferentes, separadas por superficies singulares en las que alguno de los índices está indefinido. Las simetrías discretas de este espacio de parámetros permiten reducir este número a solo 140 608 regiones independientes. En algunas de estas regiones se observan bandas de Möbius.

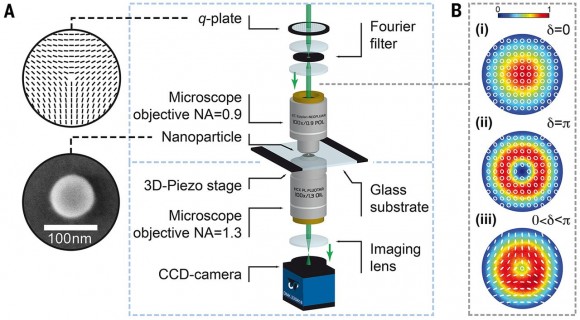
Esta figura ilustra el dispositivo experimental usado. La luz de un láser a 530 nm con polarización circular se pasa a través de una placa con q = –1/2 (q-plate o QP). Luego se pasa por un filtro de Fourier espacial que elimina los modos altos. El resultado es un haz compuesto de modos TEM y LG que se hace pasar por un microscopio con una apertura NA de 0,9 que lo hace incidir en una nanopartícula de oro esférica de 82 nm de diámetro. La luz transmitida se pasa por un microscopio con una apertura NA de 1,3. El resultado en la cámara CCD son patrones de polarización de la luz que se interpretan usando un modelo teórico. Los resultados experimentales se ajustan bastante bien a las predicciones teóricas de Freund en 2010 para haz de luz con un patrón de banda de Möbius.

En resumen, más allá de la curiosidad de lograr haces de luz tipo cinta de Möbius, el nuevo estudio muestra que es posible medir la estructura tridimensional de haces de luz con gran precisión, lo que tendrá importantes aplicaciones en metrología.