En 2014 se descubrió que el bismuturo de trisodio es una especie de grafeno tridimensional: un aislante topológico de tipo semimetal de Dirac cuyas cuasipartículas superficiales se comportan como fermiones de Dirac sin masa. Un fermión de Dirac se puede interpretar como dos fermiones de Weyl de quiralidad opuesta. Se publica ahora en Science que la aplicación de un campo eléctrico y otro magnético paralelos rompe la quiralidad y transforma los fermiones de Dirac en este material en sendos fermiones de Weyl. Un fenómeno predicho en 1983 por Holger Bech Nielsen y Masao Ninomiya.
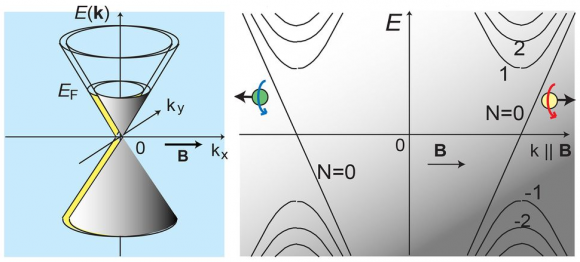
Los estados de conducción superficiales en un semimetal de Dirac corresponden a dos bandas que se cruzan en un punto de Dirac, una desde la zona de valencia a la de conducción y otra desde la de conducción a la de valencia. Al aplicar un campo magnético y un campo eléctrico las dos bandas que se cruzan se separan, resultando un semimetal de Weyl que propaga estados superficiales de tipo Weyl. Dichos estados se han observado gracias a la aparición de una magetorresistencia longitudinal negativa. Por supuesto, serán necesarios futuros estudios para confirmar el resultado usando la técnica ARPES.
Un gran resultado que confirma de nuevo que 2015 es el año de los aislantes topológicos de tipo semimetal de Weyl. El artículo es Jun Xiong et al., «Evidence for the chiral anomaly in the Dirac semimetal Na3Bi,» Science, AOP, 03 Sep 2015, doi: 10.1126/science.aac6089. Recomiendo ojear las transparencias de N. P. Ong, «Evidence for the chiral anomaly in a Dirac Semi-metal,» University of Minnesota Digital Conservancy (2015).
Una anomalía en una teoría cuántica de campos ocurre cuando una simetría de la teoría (lagrangiano) clásica no es una simetría de su versión cuántica. En los 1960 se construyó una teoría para los piones, que se interpretaron como bosones de Goldstone para la rotura de una simetría SU(2)×SU(2) en una simetría U(1)×U(1). El problema era que la tasa de desintegración de la desintegración del mesón pi neutro en dos fotones no era predicha por dicha teoría. En 1969 se descubrió que la razón era una anomalía quiral cuya inclusión clavaba los datos (Adler, 1969; Bell–Jackiw, 1969). Muchos consideran este éxito de la teoría como un paso histórico importante hacia la imposición de la cromodinámica cuántica (QCD) como la teoría correcta para la interacción fuerte entre hadrones.
Volviendo a la física de los aislantes topológicos, se predijo hace años que una anomalía quiral podría ser observada en semimetales de Dirac bajo la aplicación de un campo magnético. En el nuevo trabajo se aplica un campo eléctrico (que introduce niveles de Landau) y de forma simultánea un campo magnético paralelo que desdobla los conos de Dirac degenerados (superpuestos) en pares de conos de Weyl bien separados. Este año ha habido varios intentos de observar este fenómeno sin lograr un éxito completo.
Sin entrar en más detalles técnicos, se trata de un resultado muy interesante en uno de los campos más candentes de este año, los aislantes topológicos que son semimetales de Weyl.



He de decir que este artículo me parece poco divulgativo… nada en realidad.
Si el objetivo es dar a conocer la noticia… me he quedado helado .
Esto viene a que se dice del autor: «Quiere ser escritor de libros de divulgación científica cuando se jubile»…. y realmente parece sacado de un «Parody_generator» https://en.wikipedia.org/wiki/Parody_generator
Paco, ¿te interesa el tema?
La predicción de Nielsen y Ninomiya fue realizada en el límite «ultracuántico», omega_c \tau << 1, donde omega_c es la frecuencia de Lamor et \tau la camino libre medio de electrón. En el límite opuesto "semiclásico" de pequeño campo magnético, adecuado para el experimento, la predicción fue realizada tan tarde como 2012, usando la ecuación de Boltzmann con la fase de Berry (Ref. [9] en el artículo de Xiong et al.).
Gracias por la aclaración, Dam.
Para quien no sepa de qué va mucho el tema pero tenga conocimientos de física, recomiendo leer antes que este artículo el siguiente enlace:
http://www.investigacionyciencia.es/blogs/fisica-y-quimica/25/posts/una-nueva-revolucin-en-ciencia-de-materiales-13428
Después de leer el anterior enlace, he entendido este artículo mucho mejor.
Espero que ayude.
Salud!
Gracias, Fernando.