«Como amantes caprichosas, la mecánica cuántica y la relatividad pugnan por conseguir nuestra atención exclusiva, pero el universo las necesita a las dos. ¿Por qué? Muy sencillo: porque rigen nuestras vidas conjuntamente. [El] hombre ha recorrido un largo camino para la comprensión del cosmos. [Está] listo para emprender la búsqueda de la verdad última del universo y el todo. ¿Significa eso que la ciencia nunca dejará de hacer descubrimientos nuevos? La única respuesta que podemos dar hoy a esa pregunta es: nadie lo sabe. Aún.»
Los libros de las colecciones de RBA a veces tienen un título que confunde y un subtítulo que aclara el contenido. Arturo Quirantes Sierra, aka @elprofedefisica, «Espacio-tiempo cuántico. En busca de una teoría del todo,» Un paseo por el cosmos, Colecciones RBA (2015) [151 pp.], es un buen ejemplo. Si buscas un libro sobre la naturaleza del espacio, del tiempo, del espacio-tiempo clásico y del espacio-tiempo cuántico, lo siento, este no es tu libro. Mi buen amigo Arturo ha escrito un libro sobre la búsqueda de la teoría del todo. Por ejemplo, «espacio-tiempo» aparece por primera vez en la página 58 en su libro de 151 páginas.
La destreza como divulgador de Arturo está fuera de toda duda. Su blog «El profe de Física» es muy recomendable. Su estilo es riguroso, con tendencias hacia la ciencia ficción y con ciertas dosis de humor. No te defraudará el libro (salvo por el título). Como es amigo me permito criticarle. Yo esperaba un libro sobre la naturaleza del espacio-tiempo, desde las ideas filosóficas hasta las últimas ideas físicas. Un libro que discutiera los grandes problemas de la gravedad cuántica, la descripción cuántica del espacio-tiempo. Pero que no te engañen mis palabras, el libro está bastante bien y te lo recomiendo si quieres dar un paseo «en busca de una teoría del todo» (que no es poco).
El capítulo 1, «Las fuerzas del universo» [pp. 13-35] repasa la historia de la ciencia desde Aristóteles a Maxwell. Los aficionados a los libros de Colecciones RBA habrán leído esta historia decenas de veces escrita por multitud de autores. Arturo no ofrece nada nuevo en este tema tan trillado. Finaliza con «Hoy por hoy, todas las interacciones observadas en el universo pueden explicarse únicamente en virtud de cuatro tipos de fuerzas: gravitatoria, electromagnética, nuclear fuerte y nuclear débil. Si encontrásemos una excepción, mañana tendríamos que postular la existencia de una quinta fuerza, pero por ahora no ha sido necesario» [pág. 34].
«Espacio y tiempo; grande y pequeño» [pp. 37-65], el capítulo 2, tiene un título prometedor, pero también decepciona un poco. Discute la «catástrofe ultravioleta» como origen de la mecánica cuántica y el «problema del éter» como origen de la relatividad especial. «La relatividad general y el tejido del espacio-tiempo» [pp. 58-65] se discuten con extrema brevedad. «Fue entonces cuando el propio concepto de tiempo y espacio como entidades separadas se desvaneció. En su lugar, apareció un espacio-tiempo de cuatro dimensiones como entidad única e inseparable» [pág. 58]. «Una concepción de espacio-tiempo no plano. Desde ese momento, la imagen newtoniana de la gravedad como una fuerza de atracción desaparece. Lo que hace realmente una masa gravitatoria, según la visión einsteniana, es curvar el espacio-tiempo a su alrededor» [pág. 64].
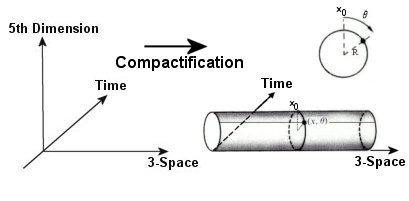
El libro se anima con el capítulo 3, «Una primera unificación: gravedad y electromagnetismo» [pp. 67-85]. «A comienzos de la década de 1910, Albert Einstein y [el físico teórico finlandés] Gunnar Nordström buscaban de forma independiente las ecuaciones de la relatividad general» [pág. 69]. David Hilbert, «Hermann Weyl y su intraducible gauge» nos llevan hacia «el asunto de las dimensiones enrolladas» [pág. 81]. «Entre otros motivos, el planteamiento de Nordström se demostró inviable porque este había utilizado la relatividad especial, de aplicación restringida. El mérito de intentarlo por vez primera en el nuevo marco teórico de la relatividad general correspondió al matemático alemán Theodor Kaluza» [pág. 81]. «Oskar Klein, un físico teórico sueco [se] convirtió en el complemento ideal para el matemático Kaluza» [pág. 82].
«La teoría de Kaluza-Klein, [con] una nueva dimensión espacial extra, [predice] la existencia de una partícula sin masa, sin carga y de espín cero que nunca había sido observada. Otro problema vino dado por el grado de compactificación de la dimensión extra. El tamaño de ese minúsculo bucle está relacionado con el valor de la carga eléctrica de las partículas y [ha] de ser idéntico para todo el espacio; algo incompatible con los principios de la relatividad general» [pág. 84].
El breve capítulo 4, «Relatividad y cuántica, ¿dos teorías incompatibles?» [pp. 87-99], nos presenta «el experimento EPR: la paradoja de Einstein, Podolski y Rosen» (por desgracia Arturo comete algunos errores conceptuales en su presentación). «Se ha de conservar la energía del sistema, pero hay otra cantidad que debe conservarse, llamada espín. [El] experimento de los fotones nos dice que esa información se transmite de algún modo mediante una ‘acción fantasma’ a una velocidad prácticamente infinita, lo que viola tanto la relatividad como el principio de localidad» [pág. 92]. «Dos partículas que han interactuado y comparten la misma función de onda (partículas entrelazadas) pueden comunicarse, aparentemente, más rápido que la luz. Como a esas velocidades superlumínicas no existe realmente transferencia de energía o de información, no se violan los principios de la relatividad general» [pág. 95]. Una pena. Gran parte del contenido entre las páginas 92 y 95 es incorrecto. Arturo comete errores de bulto, aunque se lean en muchos libros.
El título del libro «Espacio-tiempo cuántico» sugiere que versa del contenido del quinto y último capítulo, «Hacia la gravedad cuántica» [pp. 101-143]. En mi opinión, una versión de 150 páginas de este capítulo de 40 hubiera enriquecido mucho la colección «Un paseo por el cosmos» de RBA. Una oportunidad perdida. Este capítulo se inicia rotundo: «Cuando se habla de unificar la mecánica cuántica y la relatividad suele sobreentenderse que estamos hablando de la relatividad general» [pág. 103]. «En una teoría cuántica de campos el concepto de partícula deja paso al de campo» [pág. 106].
La cromodinámica cuántica da pie a un inciso sobre los nombres de los quarks. Muy divertido: «En definitiva, usando la terminología de Murray Gell-Mann y sus colegas, la naturaleza y todo lo que nos rodea está compuesta por diminutos requesones coloreados de seis sabores distintos, unidos entre sí con pegamento» [pág. 108]. Pero el capítulo 4 parece escrito con premura y contiene pequeñas erratas. Como cuando dice el «Higgs [fue] descubierto en el gran colisionador de hadrones del CERN en el año 2013» [pág. 112].
«Más allá del modelo estándar: las teorías de gran unificación» [pp. 116-120], nos habla brevemente de las GUT, cuyo «nombre no es totalmente inocente. Guts significa tripas, pero en inglés norteamericano se le asigna también el significado de tener coraje o echarle agallas a algo. Cualquier intento de ir más allá del modelo estándar significa entrar en territorio desconocido, y para intentarlo, ciertamente hay que echarle… guts» [pág. 117]. Las GUT dan pie a «La teoría cuántica de bucles (LQG), ¿una teoría del todo?» [pp. 120-125], que «parte de una visión granular del espacio. [Se] basa en la idea de que el espacio tiene escalas mínimas de tamaño» [pág. 120].
Tras discutir la radiación de Hawking y la entropía de los agujeros negros en LQG, se pasa a «Enredados en la teoría de cuerdas» [pp. 125-129] sobre la teoría de cuerdas bosónicas. «El término ‘teoría del todo’ se abrevia en inglés como TOE (Theory of Everything). La expresión inglesa on your toes (literalmente, ‘de puntillas’) se usa para expresar un estado de alerta en el que se dedican todos los esfuerzos y energía a la consecución de una meta, algo así como ‘ponerse las pilas’. Resultaría divertido descubrir que lo que nos permite estar alerta y de puntillas sea… un conjunto de cuerdas» [pág. 128]. «Otra teoría más: la supersimetría o supercuerdas» [pp. 129-133] nos menciona la teoría M: «O bien nuestro universo tiene 11 dimensiones o, sencillamente, no funciona. [La] teoría M, como cualquier otra, debe ser capaz de efectuar predicciones o, al menos, ofrecer algún modo de verificación experimental. De otro modo se quedará en mera conjetura» [pág. 133].
Finaliza el libro de Arturo con «¿Hay ciencia después de un espacio-tiempo cuántico?» [pp. 134-143], con mención a la psicohistoria de Isaac Asimov, a la armonía matemática de los cielos de Johannes Kepler y las teoría de Kurt Gödel vía ‘Esta frase es falsa’. «¿Existe la posibilidad de que suceda algo así en física? O lo que es lo mismo, ¿hay algún problema físico que no pueda en principio ser resuelto mediante teorías y matemáticas? No lo sabemos» [pág. 141].
«Si algún día el ser humano alcanza la anhelada meta de la unificación de las leyes de la física y descubre la teoría del todo, tendrá a su disposición la herramienta definitiva para profundizar en el entendimiento del cosmos. Pero será tan solo una herramienta. Las respuestas a las grandes preguntas que tanto nos intrigan deberán provenir de otra fuente. Esa es tarea de filósofos, metafísicos y pensadores» [pág. 143].
En resumen, un buen libro sobre la búsqueda de una teoría del todo que seguro que disfrutarás si te atreves a zambullirte en sus páginas.






«Esa es tarea de filósofos, metafísicos y pensadores» O sea, que nos quedaremos igual.
No olvides, Pedro, que las preguntas filosóficas las tienen que resolver los filósofos. Los físicos deben dedicarse a la física, aunque alguno pretenda hacer sus pinitos en filosofía. Los filósofos a la filosofía, aunque todos deben hacer sus deberes en física.
Sin duda muchas de las preguntas filosóficas carecen de sentido en la física, pero me cuesta pensar en las respuestas filosóficas o metafísicas como tales, en cuanto se basan en pura razón, sin evidencias. La ciencia nos ha enseñado más de mil veces de que la razón por si misma se equivoca una y otra vez.
Siempre he tenido la sensación de que la física podrá, con su lento caminar, hacerse con todo. La filosofía crea nuevas preguntas, la física las pone en su sitio.
Estoy de acuerdo aunque no soy física sino Licenciada en Letras, estoy encontrando en ella muchas respuestas para algunos temas relacionados con la literatura y el arte.
Probablemente suene demasiado optimista lo que voy a decir pero creo que la próxima gran revolución científica está ya en marcha y su «título» es precisamente «Espacio tiempo cuántico». 100 años después de la última gran revolución producida por Einstein la naturaleza del espacio-tiempo y por tanto de la gravedad está empezando a ser desvelada. En 1997 Maldacena «inició»la revolución proponiendo el «primer ingrediente» para explicar la naturaleza del espacio-tiempo con la propuesta ADS/CFT que va camino a convertirse en uno de los artículos más citados de los últimos tiempos. En 2009 Raamsdonk encontró otro ingrediente: el entrelazamiento, el mostró que sin entrelazamiento el espacio-tiempo se partiría en dos. En 2013 Susskind y Maldacena proponen otra equivalencia ER=EPR, si Einstein levantara la cabeza y comprobase que uno de sus trabajos escritos para atacar la MC iba a convertirse en un marco que puede ser fundamental para unificar MC y gravedad se quedaría de piedra. Los otros ingredientes son probablemente: cuerdas, dualidades, teoría de la información y confinamiento. Ahora los Físicos pueden hacer cosas que hace 1 década eran impensables: controlando ciertos aspectos de las interacciones de las partículas en un marco CFT pueden cambiar y predecir ciertos aspectos cuánticos de la gravedad en un marco ADS. Ciertas conclusiones de esta nueva revolución parecen de ciencia ficción: La gravedad «emerge» como resultado de la interacción entre partículas que viven en el borde conforme, todas las partículas entrelazadas están unidas por un agujero de gusano, las etapas de confinamiento-deconfinamiento en QCD son equivalentes a distintas fases dentro de distintos agujeros negros… Por supuesto, aún falta mucho trabajo y estas ideas aún están por desarrollar y verificar pero creo que muchos Físicos piensan que algo «muy gordo» está en marcha y que concluirá con una revolución mayor que la que produjo Einstein. El próximo gran avance podría ser encontrar el equivalente del principio holográfico en nuestro Universo en expansión, entender el papel del entrelazamiento y entender que significan las dualidades que parecen ser una extraña propiedad de nuestro Universo. La próxima revolución está en marcha y promete cambiar para siempre nuestra imagen del Universo y del espacio-tiempo.
PD: Para los que quieran empezar a entender algo de todo esto recomiendo:
http://www.sciencenews.org/article/entanglement-gravitys-long-distance-connection
http://www.nature.com/news/the-quantum-source-of-space-time-1.18797
Planck, estoy de acuerdo, estamos en uno de los momentos más apasionantes de la física del siglo XXI. La gravedad emergente a partir de la entropía o del entrelazamiento o del principio holográfico nos están ofreciendo caminos hacia la gravedad cuántica que no podíamos soñar hace 15 años. Desvelar la naturaleza cuántica del espaciotiempo es un paso clave en el camino hacia el futuro de la física en el siglo XXI.
Qué gusto, da, Plank, leerte; la pasión que le pones a todo.
Qué lástima que las cosas se complican ya tanto, que aquellos de nosotros que aun siendo físicos de formación, debemos ocupar nuestra mente en otro quehaceres, nos vamos perdiendo en esta gran amalgamas de nuevas ideas.
Muchas gracias Pedro. Como ya he dicho en alguna ocasión creo que los detalles son bastante complejos pero las ideas generales no lo son.
Un saludo.
Y también casualmente por esa misma época
The life of the cosmos (1997), Lee Smolin
PART 4
EINSTEIN’S LEGACY
What are space and time?
bla bla bla
The Dalai Lama
SIXTEEN
SPACE and TIME in the NEW COSMOLOGY
Newton bla bla bla
Leibniz bla bla bla
atomismo bla bla bla
relacionismo bla bla bla
Einstein bla bla bla
Newton bla bla bla
Leibniz bla bla bla
¿? No entiendo nada, Gastón.
Me quedo descolgado del comentario de mas arriba pero están relacionados. He aquí la aclaración (tratare de no ser muy extenso para no aburrirlos).
El comentario de Juan Maldacena, (http://casanchi.com/fis/anegros01.pdf) esta íntimamente vinculado con la idea que se tiene de que el espacio, el tiempo y la materia son conceptos prefísicos, esto es, conceptos fundamentales en los que se basa todo el andamiaje teórico de la ciencia. Deriven por ustedes mismos estas consecuencias.
El comentario sobre libro de Smolin es un chascarrillo. En las 10 paginas que debería tratar sobre la naturaleza del espacio y el tiempo versa sobre historia, la separación entre Newtonianos versus Leibnizianos y como estos tenían una concepción opuesta o si prefieren, diferente de lo que es le espacio y el tiempo, por lo que es decepcionante para los que esperan encontrar una respuesta concreta.
(en el capitulo encontramos que «los conceptos de espacio y tiempo, como el concepto de sociedad, son conceptos abstractos y similares…», etc.)
Recientes estudios ponen en duda estas afirmaciones y asumen que el concepto de Leibniz del espacio fue sufriendo modificaciones a lo largo de su obra, en contra de lo que algunos de sus comentaristas en el siglo XX afirman; este concepto difiere del concepto newtoniano del espacio, especialmente en cuanto a su aspecto metafísico, pero no en su apariencia física, por lo que ambos filósofos estaban más cerca de lo que cabría pensar. La construcción real de la física matemática en la era barroca apunta a Descartes y a los cartesianistas (y no a Newton) como el gran rival de Leibniz. En definitiva, entre Leibniz y Newton, en lo que respecta al concepto de espacio, no habría discrepancias y si similitudes físicas, mientras tanto divergen ambos conceptualmente de Descartes.
Me sorprende todo esto porque Newton nunca se tomo en serio estas discrepancias con Leibniz. Convengamos que un científico que hace escribir a sus amigos o estudiantes las cartas en una discusión ¡no le interesa para nada el tema de la misma! (hablando en familiar, ¡Newton le tomo el pelo a Leibniz!).
Lo único rescatable del capitulo de Smolin es la aclaración de que en el siglo 20 se tenía la visión del mundo compuesto por partículas elementales (atomismo)
que se mueven en el espacio-tiempo de la TGR de Einstein (relacionismo) y que el modelo estándar de la física de partículas es relacionista en el uso del principio gauge pero atomista en la descripción de las partículas. Por lo que atomistas y relacionistas no estaban tan enfrentados como en otras épocas y trabajaron juntos para tratar de desentrañar el misterio del universo. A, y una mención de la complejidad, pero nada mas.
Bueno, la peluca.
Gastón, el artículo que citas de Maldacena se refiere (salvo el último párrafo) al espacio-tiempo clásico de Einstein. La naturaleza del espacio-tiempo cuántico solo se menciona en el último párrafo, y de pasada, cuando habla de «moléculas de agua yendo y viniendo» que describen la física íntima del «agua líquida» que parece continua. Se refiere a que el espacio-tiempo emerge de la interacción entre cuerdas cerradas en teoría de cuerdas. Menciona su conjetura AdS/CFT que dice que una teoría de cuerdas en 1+1 (que es una teoría de campos conformes, o CFT) es equivalente a una teoría de un espacio-tiempo con curvatura negativa (un espacio-tiempo tipo Anti-de-Sitter, o AdS). «A mayores escalas, nuestro universo parece más un espacio-tiempo curvado positivamente.» Quiere decir que a la escala de energías de la cuerda (sea Ms) el espacio-tiempo que conocemos no existe, solo hay cuerdas y un espacio-tiempo «efectivo» o «aproximado» de tipo AdS (muy diferente de nuestro espacio-tiempo actual).. A una escala mayor de Ms (no se sabe bien cuál, lo tiene que decidir el experimento, pero se estima entre 10 y 100 veces Ms), emerge un espacio-tiempo de curvatura positiva como el de la teoría de la relatividad de Einstein que observamos a muy baja energía (comparada con Ms) en la actualidad. «Tal descripción, si existiera, resolvería el problema de la singularidad del Big Bang» y, en teoría de cuerdas, todos los problemas asociados a las singularidades en la teoría de Einstein.
Saludos
Francis
Si, Francisco. Es valida tu observación. Sucede que no quería considerar el «espacio-tiempo cuántico» (por eso la similitud de las fechas en los dos textos y el extracto del párrafo coincidiendo con el contenido de lo que versa el capitulo de Smolin). Como bien mencionaste tu, es exigua la descripcion de Maldacena en el articulo que linkie sobre el «espacio-tiempo cuántico».
Coincido con Francis. Esperaba mucho más de este libro. Lamentablemente es el más flojo, hasta ahora, de la colección.
Ed, ¿has leído «Universos paralelos» de José Rodríguez-Quintero? Habrá reseña la semana próxima. No quiero adelantar mi opinión.
No, no lo heleído Francis. Pero por la forma de decírmelo me imagino que no te habrá gustado mucho.
Dijiste: «Yo esperaba un libro sobre la naturaleza del espacio-tiempo, desde las ideas filosóficas hasta las últimas ideas físicas. Un libro que discutiera los grandes problemas de la gravedad cuántica, la descripción cuántica del espacio-tiempo.»
Yo estoy interesado en leer algún libro que aborde el tema del espacio-tiempo EXACTAMENTE de esa manera. Me gustaría saber si has leído alguna vez algún libro parecido y cómo se llama.
En filosofía, los libros de Kant «Crítica de la razón pura» y «Prolegómenos a toda metafísica futura que pueda presentarse como ciencia» (versión reducida por el propio Kant y más simplificada de la «Crítica de la razón pura»), cuando éste habla de la Estética Trascendental, trata ya el tema del espacio-tiempo. Pero me encantaría encontrar algo más extenso que llegue hasta nuestra época y que incluya ideas y conceptos científicos actuales.
Muchas gracias y enhorabuena por este magnífico Blog! Un saludo!
Tati, en español no conozco ninguno específico, salvo los enfocados a la teoría de cuerdas, como Brian Greene, «El tejido del cosmos: Espacio, tiempo y la textura de la realidad», que si no lo conoces te gustará mucho. Si quieres un libro que no esté enfocado en la teoría de cuerdas, debes recurrir al inglés. Está bien el de Lee Smolin, «Three Roads To Quantum Gravity».
Por supuesto, si mencionas a Kant, lo mismo te refieres a libros que no sean de divulgación. Monografías técnicas hay muchas (dependiendo de tu nivel de matemáticas y de física). Si prefieres algo filosófico, escrito por un filósofo, te recomiendo la tesis doctoral de Tiziana Vistarini, «Emergent spacetime in String Theory» (100 pp.).
Francis, ahora que estamos en el centenario de la relatividad generalizada, yo estoy muy burro con el tema de que se reconozca a Emmy Noether. Creo que nunca Einstein pudo llegar a la libertad de comprender relacciones físicas sin Emmy. De hecho, fueron amigos.
Gustavo, ¿exactamente qué quieres que se le reconozca? Hoy en día es la matemática más famosa del siglo XX.
Emmy Noether fue invitada a unirse al grupo de David Hilbert en Gotinga en 1915 (se incorporó a principios del verano). Tenía 33 años y había realizado su tesis doctoral 7 años antes bajo la dirección de Paul Gordan. Tras su llegada a Gotinga asistió a las 6 charlas que impartió Albert Einstein sobre sus progresos en la teoría general de la relatividad. En noviembre de 1915, tras el éxito de Einstein, Hilbert puso a Noether a estudiar el trabajo de Einstein, en especial, el problema de la energía (la mayor crítica de Hilbert al trabajo de Einstein). Se sabe que trabajó entre 1915 y 1916 en el problema de la energía en relatividad general y que ello le llevó a sus famosos dos teoremas de 1918. Pero entre 1915 y 1918 no me consta que publicara nada sobre relatividad. Einstein estuvo a punto de obtener el primer teorema de Noether alrededor de 1913, pero no tenía el dominio de la teoría de grupos de Noether, Klein y otros.
Tres veces he intentado meterme a fondo con el teorema de Noether…¡la madre que me hizo! Menuda capacidad de abstracción tenía esa mujer…
Pedro, ¿has estudiado teoría de grupos? Klein mostró que la simetría es equivalente a lo invariante a la acción de un grupo y Noether siguiendo esta línea mostró que lo invariante a la acción de un grupo de simetría en física implica una ley de conservación de algo que se conserva (carga). Hoy en día, en el contexto de la teoría de grupos, el resultado de Noether es trivial. A principios del siglo XX la teoría de grupos (aunque tenía sus raíces en el trabajo de Lagrange, Abel y Galois) era un campo emergente en matemáticas y solo unos pocos matemáticos conocían este campo tan abstracto (Klein, Cayley, Artin, Noether, …).
Estudiar teoría de campos tal cual haría un matemático, es decir, haciendo los deberes, efectivamente no.
Me alegra saber que ahora es trivial.
Si me tocara la primitiva, cosa que obviamente no va a ocurrir, lo primero que haría sería graduarme, masterizarme y supermineralizarme en matemáticas.
Pedro, cuando yo era niño se estudiaba qué eran los grupos en EGB (educación básica para niños de menos de 10 años). La teoría de grupos se podía introducir (aunque no se hacía, no sé el porqué) en educación secundaria. La aplicación de la teoría de grupos en el teorema de Noether es muy sencilla y asequible a cualquier estudiante de primer curso de la licenciatura de matemáticas (al menos cuando yo estudiaba, ahora han cambiado los temarios y se estudia en segundo curso del grado).
Francis, está claro que todos hemos visto en el colegio lo que es un grupo, yo soy licenciado en físicas, y aunque no hice teóricas, también me encontré con este tipo de estructura algebraica…pero de verdad, no me parece el teorema tan sencillo como todo eso… está involucrado el Lagrangiano, los grupos de Lie….
¡Ché! a mi me resulta complejo pillarle la esencia, tal vez sea muy exigente y no me contente con la idea más global…
Pedro, hay muchos libros de grupos y álgebras de Lie para físicos. Conocer el origen de la conservación de la energía, del momento lineal y del momento angular gracias al teorema de Noether debería ser obligado para todos los licenciados en Física (se puede impartir en mecánica de segundo curso cuando se presenta la formulación lagrangiana).
Cierto que debería ser obligado, sin duda alguna. Yo me licencié en la universidad de Valencia, en la especialidad que había entonces llamada «Electricidad y Magnetismo, Electrónica e informática» (las otras eran «Teóricas» y «Fundamental»). No recuerdo haber dado el teorema de Noether en mecánica, Aunque estoy seguro de que en Métodos matemáticos I, II o III debimos de ver al amigo Lie, seguro.
Francis, no crees que una vez llegue a formularse la «Teoría Del Todo», hecho que espero con cierta ansiedad pues todo apunta a que es inminente, sobre COMO funciona el Universo, COMO se creó y COMO se destruirá; yo, una lega en Física pero ávida lectora de tus artículos, levantaré la mano y preguntaré: y ¿POR QUÉ?
(Perdonad las mayúsculas, pero quería dar énfasis)
Es decir, la cuestión de la Voluntad desencadenante o inherente ¿se resolverá?
No, Amanda, una «teoría del todo» (es decir, una teoría que describe con los mismos objetos fundamntales el espaciotiempo y los campos cuánticos) no aportará ninguna información sobre cómo funcional el universo, cómo se creó o cómo se desturirá. Un nuevo paradigma (una «teoría del todo» lo será) nos permite saber qué preguntas podemos hacer y qué respuestas esperamos poder obtener, pero no nos ofrece estas respuestas, salvo gracias a las observaciones y los experimentos. Si mañana logramoas una teoría del todo, habremos dado el primer paso de un proceso que puede suponer siglos de trabajo científico para desvelar las respuestas.
Francis, aunque mencionas en la respuesta a GustavoCarra (22 Nov) ‘sus [de Noether] dos famosos teoremas’, y la sitúas a ella como la más famosa matemática del S. XX, el resto de tus comentarios en este asunto puede llevar a pensar que el contenido de esos resultados se reduce básicamente al que se estudia en las asignaturas de grado de Física o de Matemáticas: la relación directa entre la existencia de cantidades conservadas en un sistema lagrangiano de número finito de libertades con la presencia de grupos uniparamétricos de simetrías del sistema. Esa idea la refuerzas cuando dices que ‘hoy en día, en el contexto de la teoría de grupos, el resultado de Noether es trivial’ o que es una aplicación ‘muy sencilla y asequible a cualquier estudiante de primer curso de la licenciatura de matemáticas’.
Creo que esa simplificación no hace la debida justicia a la memoria de Noether ni a sus resultados.
Es cierto que hoy en día lo que Noether llamó Teorema I es ‘relativamente’ trivial en los casos de numero finito de libertades, y que debería obligatoriamente verse en la licenciatura (y creo que seguramente se ve en casi todas las universidades). No es ya tan trivial si se trata de un campo, con infinitas libertades y en el que lo que hay no son cantidades sino corrientes conservadas. Pero es que el alcance del otro teorema, el Teorema II de Noether está, completamente, en otro nivel. Y el segundo teorema fue en su momento un auténtico tour de force (ese trabajo es una de las contribuciones por las que EN fué una matemática excepcional), que se separa en planteamiento y en alcance bastante estratosféricamente del teorema ‘de juguete’ que se estudia en licenciatura o grado.
En ambos casos, las aplicaciones más destacadas a la física son cuando las simetrías son de una u otra manera de tipo gauge. Basta leer las seis lineas de la entrada ‘Noether’s second theorem’ en la Wikipedia (en inglés) para sospechar que ese teorema II juega en otra división. Y si se quieren confirmar las sospechas, basta echar una ojeada al artículo de Noether de 1918, disponible en ArXiV http://arxiv.org/pdf/physics/0503066.pdf
Cedo la palabra a Emmy Noether en ese artículo:
«With these supplementary remarks, Theorem I comprises all theorems on first integrals known to mechanics etc., while Theorem II may be described as the utmost possible generalization of the “general theory of relativity” in group theory.»
Y me temo que este segundo teorema, se mire como se mire, ni es hoy en día trivial ni está al alcance de estudiantes primer curso de licenciatura ….
Gracias, MarianoS, por tu comentario. Si conoces el segundo teorema de Noether sabrás que es trivial (aunque si lo encuentras escrito en su versión más general requiere saber lo que es un álgebra de Lie).
Nunca diré que el trabajo de la genial Noether es trivial, todo lo contrario, su trabajo es extremadamente no trivial (por ello es una de las matemáticas más importantes de toda la historia de la humanidad). Lo que he dicho y me reafirmo es que sus dos teoremas que relacionan simetrías e invariantes son triviales (un siglo después de haber sido formulados). Que no es lo mismo.
Francis, gracias por la respuesta. No está en mi ánimo entrar aquí en ninguna discusión, ya que aprecio tu trabajo en lo mucho que vale en poner al día al procomún de las novedades científicas interesantes.
Pero me parece que tu respuesta deriva lateralmente en vez de entrar en el fondo de mi comentario. Entiendo que haciendo tú esta tarea gratis et amore, no nos asiste a los comentaristas ningún derecho adicional: yo comenté en este caso porque Pedro Mascarós había ya expresado sus dudas sobre que el asunto fuera tan trivial. Y añado que tú además sueles responder a los comentarios, lo que es muy de agradecer.
Diciendo, en condicional ‘si conoces el segundo … sabrás que es trivial … requiere saber qué es un álgebra de Lie’, estás desautorizando mi comentario (en términos ‘efectivos’) por el expediente de transmitir al personal que probablemente yo no sé qué es el segundo teorema de Noether (pues si lo supiera sabría que es trivial), que tú sí que lo sabes (y además sabes que es trivial) y que yo necesitaré saber ( 🙂 ) lo que es un álgebra de Lie para leerlo escrito en su versión más general. Vale, pues te aseguro que como adivino esta vez no has acertado. Conozco el segundo teorema de Noether yo diría que bastante bien pues lo he estudiado a fondo (el Teorema II sí, no el I), en el contexto de la teoría cuántica de campos. Por ello creo saber positivamente que el Teorema II no es nada trivial: ni en época de Noether ni ahora. Y he tratado y escuchado a bastante gente del gremio que también lo conoce bien, y a nadie le he oído siquiera insinuar que hoy en día ese resultado en concreto sea trivial. Otra cosa es que hoy se entienda más fácilmente, claro
Ese segundo teorema no relaciona tan directamente como el I simetrías e invariantes, que es lo que tu dices y te reafirmas en tu respuesta que es trivial (y que yo diría que es solo ‘relativamente trivial’, aunque en esa parte estamos esencialmente de acuerdo). Mi comentario se centraba en el Teorema II que es cosa muy a otro nivel: establece ciertas identidades diferenciales que son consecuencia automática de la invariancia del funcional de acción asociado a ciertas densidades lagrangianas bajo transformaciones que dependen de varias funciones arbitrarias y de sus derivadas. En el caso de la acción de Einstein-Hilbert y del lagrangiano de la RG, estas identidades ‘de Noether’ son las identidades de Bianchi de la geometría pseudoriemanniana.
¿Trivial? Si lo sigues afirmando, no seré yo quien te contradiga más. Quizás entendemos por trivial cosas distintas.
Saludos cordiales