Ya puedes escuchar el podcast iVoox del Programa 139 de La Fábrica de la Ciencia, “100 años de Relatividad General de Einstein», en el que Jorge Onsulve Orellana, aka @jonsulve, me ha entrevistado sobre el tema del día. Como siempre una transcripción libre más abajo.
Recomiendo leer a Jorge Zuluaga, aka @zuluagajorge, «Cronología de un Milagro,» Trinoceronte, 25 Nov 2015.
Para quiera disfrutar de una lectura más sosegada y técnica recomiendo encarecidamente Galina Weinstein, «From the Berlin «ENTWURF» Field Equations to the Einstein Tensor I: October 1914 until Beginning of November 1915,» arXiv:1201.5352 [physics.hist-ph]; «From the Berlin «Entwurf» Field Equations to the Einstein Tensor II: November 1915 until March 1916,» arXiv:1201.5353 [physics.hist-ph]; «From the Berlin «Entwurf» Field Equations to the Einstein Tensor III: March 1916,» arXiv:1201.5358 [physics.hist-ph].
El 25 de noviembre se cumplen los 100 años de las ecuaciones de Einstein de la relatividad general. Einstein las hizo públicas ante la Academia Prusiana de las Ciencias el 25 de Noviembre de 1915. Su Annus Mirabilis fue en 1905, cuando publicó la teoría de la relatividad especial. ¿Por qué Einstein se vio obligado a generalizar la teoría especial y obtener la teoría general? Un malentendido bastante popular afirma que la teoría especial solo se aplica a sistemas de referencia inerciales (no acelerados) y la general a los no inerciales (acelerados). Esto es un mito. Igual que los postulados de la teoría de Newton se presentan en el caso de sistemas inerciales, pero se pueden usar con cualquier sistema no inercial. Los postulados de la teoría especial de Einstein también se presentan en el caso de sistemas inerciales, pero se pueden usar con cualquier sistema no inercial o acelerado. Igual que en el caso de Newton en los sistemas no inerciales aparecen fuerzas ficticias (o fuerzas no inerciales), pero el formalismo se puede aplicar sin ningún problema. La teoría general de la relatividad es una teoría de la gravitación. Newton ya introdujo el principio de equivalencia que afirma que localmente un campo de gravedad se puede anular usando un sistema acelerado. Este principio significa que la gravedad y la inercia en un espaciotiempo curvos son equivalentes, localmente, es decir, en una región pequeña del espaciotiempo la gravedad se puede anular, luego parece una fuerza ficticia, sin embargo, no se puede anular la gravedad de forma global. Por tanto, la gravedad es una fuerza fundamental en física como el electromagnetismo o las fuerzas nucleares.
Einstein necesitó 10 años desde 1905 hasta 1915 para desarrollar la teoría general de la relatividad. ¿Cuáles fueron los eventos más trascendentales durante estos años? La gravedad de Newton se puede incorporar en la teoría de la relatividad especial dando lugar a una teoría de la gravitación postnewtoniana. La fuerza de Newton proporcional a la inversa del cuadrado de la distancia se corrige con un término cúbico. Esto explica el desplazamiento del perihelio de Mercurio y toda la física gravitatoria en el sistema solar. Sin embargo, desde un punto de vista conceptual, esta teoría tiene problemas conceptuales. Por ello Einstein decidió obtener una teoría de la gravitación relativista más allá de las ideas de postnewtonianas. Entre 1907 y 1912 … sin éxito. Pero en 1912 decidió que debía generalizar la covariancia de la relatividad especial en el espaciotiempo de Minkowski a una covariancia más general en un espaciotiempo curvo. Entre 1912 y 1914 colaboró con su amigo matemático Marcel Grossmann quien le recomendó usar la geometría de Riemann. Einstein y Grossman publicaron en 1913 una teoría de la gravedad “preliminar” (Entwurf en alemán), hoy llamada la teoría de Einstein-Grossmann. Esta teoría tenía ciertos defectos, destacando que sus ecuaciones no eran covariantes. Al aplicarla al movimiento anómalo de Mercurio (con ayuda de su amigo Michele Besso) el resultado en lugar de ser de 43 segundos de arco por siglo era de solo de 18 segundos de arco. Algo estaba mal. La situación cambió radicalmente gracias a tres artículos que Einstein publicó en noviembre de 1915 que le permitieron obtener una teoría covariante para la gravedad.
Un mes intenso, ¿qué aportó el primero de los tres artículos de Einstein en noviembre de 1915? En julio de 1915, el famoso matemático David Hilbert invitó a Einstein a impartir una serie de conferencias sobre su teoría general de la relatividad. El trabajo que presentó no convenció a Hilbert, que le comunicó en octubre de 2015 que tenía defectos graves desde el punto de vista matemático (Einstein no los entendió hasta la primavera de 2016). Sin embargo, Einstein trabajó muy duro durante el mes de octubre y el jueves 4 de noviembre de 1915, logró obtener una versión covariante de sus ecuaciones, aunque bajo una condición restrictiva, la unimodularidad de la métrica. El domingo 7 de noviembre de 2015 Enstein envió una carta a Hilbert con sus nuevos aportes. El miércoles 10 de noviembre Einstein recibió la respuesta, Hilbert también estaba trabajando en su propia versión de una teoría unificada del electromagnetismo, la gravedad y la materia. Hilbert se había inspirado en Einstein, pero Einstein lo vio como un competidor que le sirvió de aliciente para conseguir en un tiempo récord la versión definitiva.
¿Gracias a ese incentivo surgió el segundo artículo del mes de noviembre de 1915? Exactamente, el jueves 11 de noviembre de 1915, Einstein publicó una adenda (Nachtrag en alemán) a su artículo del jueves 4 de noviembre. Esta explicaba las condiciones físicas claves detrás de su formulación matemática. La física era la gran ventaja de Einstein sobre las matemáticas de Hilbert. La métrica del espaciotiempo equivale al potencial del campo gravitatorio y la conexión de Levi-Civita eran equivalentes a las fuerzas no inerciales asociadas al principio de equivalencia. Gracias a esta idea Einstein descubrió que la importancia del tensor de Ricci para describir la curvatura del espaciotiempo. Pero mantuvo las ecuaciones que requerían que la métrica fuera unimodular (luego no eran ecuaciones del todo covariantes). La fuente de la gravedad para estas ecuaciones, el tensor de energía-momento tenía que tener traza nula (como en el caso del electromagnetismo), pero esta condición no se cumple para la materia. Había que cambiar las ecuaciones para lograr la covariancia incluso para la materia. La física guiaba a Einstein, mientras que Hilbert era guiado por las matemáticas.
Y llegamos al tercero y último artículo de noviembre de 1915 en el que Einstein presentó las ecuaciones definitivas de la teoría general de la relatividad. Hilbert invitó a Einstein a asistir a una charla sobre sus propios avances, pero Einstein estaba agotado físicamente con el esfuerzo de desarrollar su teoría y declinó la invitación (no podía visitar Gotinga). El 20 de noviembre Hilbert presentó su teoría, pero no incluía las ecuaciones correctas (aunque cuando lo publicó por escrito el 6 de diciembre, sí las incluyó, por lo que hay quien las llama ecuaciones Hilbert-Einstein). Einstein siguió trabajando hasta llegar a la versión covariante actual de sus ecuaciones. El 18 de noviembre logró explicar la precesión del perihelio de Mercurio. Y el jueves 25 de noviembre de 1915 Albert Einstein explicó en una conferencia ante la Academia Prusiana de Ciencias, en Berlín, las ecuaciones definitivas de su teoría general de la relatividad. Tras casi una década de tortuosos intentos y con el matemático David Hilbert pisándole los talones, por fin logró una de las cimas intelectuales de la humanidad.
¿Cómo se puede explicar en un lenguaje sencillo el significado de la ecuación de Einstein para la gravedad? Se suele decir que la masa le dice al espacio-tiempo como curvarse y éste le dicta a la masa cómo moverse. En realidad es un sistema de diez ecuaciones no lineales acopladas, Rμν – 1/2 gμν R = 8π G Tμν. La ecuación relaciona la curvatura del espacio-tiempo ↔ energía (masa). Newton no explica qué es la gravedad. Einstein logra explicarla gracias a la curvatura del espaciotiempo.
¿Qué cuáles son las diferencias más importantes entre la teoría de Newton y la teoría de Einstein? La gravedad deja de ser una acción a distancia e instantánea para convertirse en la acción local de la curvatura del espaciotiempo y que se mueve a la velocidad de la luz en el vacío. Además, la fuente de la gravedad no es la masa (la «carga» newtoniana) sino la energía (tensor energía-momento).
La visualización de la curvatura del espacio-tiempo como una cama elástica deformada por el peso de una masa grande en la que se mueven unas canicas, ¿permite entender bien la gravedad de Einstein? Aunque ilustrativa, esta analogía no transmite lo esencial de la teoría, que la curvatura del espacio-tiempo se concentra en la dirección del tiempo y no del espacio. La gravedad es sobre todo curvatura en el tiempo. Nos movemos mucho más en el tiempo que en el espacio. Una aplicación práctica de ello, la más famosa, es el navegador GPS. El efecto es pequeñísimo, pero medible, de la curvatura del espacio-tiempo alrededor de la Tierra sobre la señal que se recibe de los satélites.
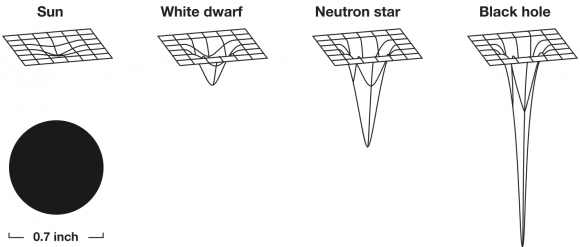
¿Qué relaciona la relatividad general con los agujeros negros? En una carta fechada el 22 de diciembre el astrónomo alemán Karl Schwarzschild le comunicó a Einstein que había encontrado una solución exacta a sus ecuaciones para la gravedad de la Tierra, el Sol, o las estrellas. Su solución contenía un horizonte y daba lugar a lo que ahora llamamos agujeros negros.





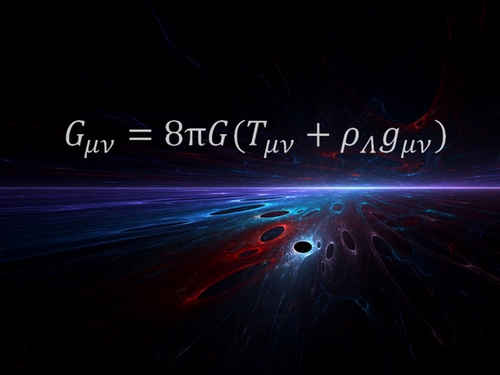


Saludos señor Francis, estuve en una de sus charlas hace poco en un pub de teatinos muy entretenida sobre el LHC y las partículas subatómicas, me gustó mucho y me gustaría poder volver a estar presente en una venidera.
Le escribo para comentarle que se le han colado en el texto algunas erratas:
«David Hilbert invitó a Einstein a impartir una serie de conferencias sobre su teoría general de la relatividad. El trabajo no convenció a Hilbert, que afirmó en octubre de 2015 que tenía defectos graves, que Einstein no entendió hasta la primavera de 2016. Sin embargo, Einstein trabajó muy duro y el jueves 4 de noviembre de 1915, logró obtener una versión covariante de sus ecuaciones, aunque para bajo una condición restrictiva, la unimodularidad de la métrica. El domingo 7 de noviembre de 2015 Enstein envió una carta a Hilbert.»
No he podido evitar reirme un poco xDDD.
Estaré atento a más entradas suyas que son la mar de interesantes.
Saludos 😉
Gracias, David.
Nunca he podido entender, si el tiempo está incluido en la topología espacio-tiempo del universo ¿como pueden describir la historia del universo partiendo del BigBang mediante una cronología?, es como tener de parámetro un tiempo (absoluto) externo al universo para contar la historia de espacio-tiempo y su evolución (no es coherente).
Reneco, en cosmología se usan coordenadas comóviles, es decir, el «tiempo» mide la «escala» de la expansión (este tiempo no es la noción de tiempo que tenemos nosotros hoy en día, aunque se ajusta para que en el presente coincidan ambas nociones). Más información divulgativa. Desde un punto de vista técnico el «tiempo comóvil» requiere fijar una escala para el universo y si se fija la escala actual, dicho «tiempo» coincide con la noción de tiempo actual. Más información divulgativa.
Por supuesto, ante la duda, recurre a cualquier libro de texto de cosmología. Todos empiezan por el principio, la noción de espaciotiempo en cosmología.
Voy a tratar de enganchar en el tema, pero los textos de cosmología asumen sin explicar algo que es incoherente «el universo se expande» (en el ahora) como si mi tiempo fuese el mismo para una galaxia lejana en el pasado. Un ejemplo ¿puedo decir que Napoleón se está acercando o alejando de mí, si Napoleón está muerto (solo existe en el pasado)?, la analogía es valida para una galaxia lejana
El efecto Doopler Zombie.
«el universo se describe a si mismo bajo el parámetro tiempo», ¿eso es recursividad?.
«Nos movemos mucho más en el tiempo que en el espacio.» Nuestro concepto de movimiento está tan enraizado al de velocidad, que expresar esta idea sin levantar confusión es muy complejo de verdad; pero muy cierta a fin de cuentas. Gran frase.
Perdón… 8 minutos 34 segundos, tardaría en notarlo la Tierra no 4 (El Sol está a una media de 150 millones de km)
¿Que les parece esto? Es un estudio publicado en la revista Classical and Quantum Gravity.
(aqui el articulo http://iopscience.iop.org/article/10.1088/0264-9381/32/17/175003/meta;jsessionid=3A562B0DBCC6903B3802F593B31B3912.c1, )
¿De que trata?. Que a suficientemente altas aceleraciones, las capacidades operativas de cualquier teoría construida sobre la noción del tiempo, y por lo tanto también del espacio, se interrumpe.
«Si nuestras predicciones se confirman experimentalmente, muchas cosas relacionadas con nuestra comprensión del espacio-tiempo, el paso del tiempo, y sus métodos de medición deberán ser repensados desde cero».
Gastón, el tiempo es lo que miden los relojes. En teoría, si no puedes construir un reloj en cierta época del universo, el tiempo no puede existir. El tema de los relojes ideales ha dado para cientos de artículos en los últimos años. En ciertas épocas del universo construir un reloj ideal requiere gran número de sutilezas.
El nuevo artículo afirma que los relojes ideales acelerados sufren el efecto Unruh y dejan de ser ideales. Lo que no quita que los relojes ideales no acelerados, que no sufren dicho efecto, puedan ser tan ideales como se quiera.
Pero, cuidado, el nuevo artículo (aunque esté firmado por Dragan), es muy especulativo. Classical and Quantum Gravity publica muchos artículos especulativos (su revisión por pares es bastante laxa), que revistas más prestigiosas no superarían la revisión por pares (por falta de rigor). Así que, mientras estos cálculos cuasiclásicos no se hagan con mayor rigor, no debemos preocuparnos por frases tan grandilocuentes como la que has traducido.
Francisco, esa es una definición operacional del tiempo.
Tiempo: lo que mide el reloj.
Reloj: lo que mide el tiempo.
Longitud: lo que mide la regla.
Regla: lo que mide la longitud.
Peso: lo que mide la balanza.
Balanza: lo que mide el peso.
Temperatura: lo que mide el termómetro.
Termómetro: lo que mide la temperatura.
Y así con todas las magnitudes…
Un físico experimental puede quedar conforme con estas definiciones. Medir es el principal objetivo para la física experimental. Lo que no se puede medir, para un físico experimental, no existe.
Pero, ¿Coincidimos en que una teoría no se construye solo con datos empíricos, y que la realidad puede contener parámetros o propiedades no medibles?.
Definiciones de diccionario barato comprado en un kiosco. Yo también tengo uno en casa…lo uso para que no se me vuelen los papeles…
Respecto a la referencia que se hace en este artículo al sistema GPS (como supuesta prueba de la relatividad del tiempo), quería decir lo siguiente:
En los relojes atómicos de los satélites GPS se observó que se producía un adelanto diario de unos 38 microsegundos, de modo que se tuvo que alterar ligeramente la frecuencia de oscilación de estos relojes para que no fueran acumulando un desfase con respecto a los relojes situados en la Tierra.
Ahora bien, en la página-web del NIST (el organismo que trabaja actualmente en la mejora de los relojes atómicos) se dice que estos relojes son muy precisos pero no llegan a ser totalmente perfectos, ya que su frecuencia de oscilación se ve ligeramente alterada por la gravedad, los campos magnéticos, los campos eléctricos, la fuerza, el movimiento, la temperatura y otros fenómenos (véase http://www.nist.gov/pml/div688/2013_1_17_newera_atomicclocks.cfm ).
Lógicamente las condiciones físicas que soportan los relojes atómicos en los satélites GPS no son las mismas que las de los receptores situados en la Tierra, y por ello hay que tener en cuenta los problemas que se presentan en el propio funcionamiento de los relojes. Sin embargo, los físicos relativistas atribuyen la totalidad de esos 38 microsegundos de adelanto (los que tuvieron que corregirse en los relojes de los satélites) a la relatividad del tiempo, como si los márgenes de error de estos relojes no existiesen.
Por su parte, el físico que creó en 1955 el primer reloj atómico de cesio (llamado Louis Essen) vivió hasta 1997 y nunca creyó que los relojes atómicos hubiesen demostrado la relatividad del tiempo (véase http://es.wikipedia.org/wiki/Louis_Essen ).
Si situásemos un reloj de luz (también conocido como “reloj ideal de Einstein-Langevin”) en la misma órbita del satélite GPS, este reloj sólo tendría un modo de verificar el adelanto diario de 38 microsegundos: modificando el valor de la luz en el vacío (la famosa constante c) y contradiciendo así el segundo postulado de la Teoría de la Relatividad. Es decir, que un reloj de luz que cumpliera estrictamente los postulados relativistas no podría adelantarse del mismo modo que lo hace el reloj atómico de cesio en la órbita del satélite GPS.
En el caso del reloj de péndulo (cuyo uso era muy habitual en la época de Einstein), este tipo de reloj tendría un ritmo más lento con menor gravedad, al contrario de lo que le ocurre al reloj atómico de cesio. Si “el tiempo es lo que miden los relojes” y el tiempo debe transcurrir un poquito más rápido en la órbita de los satélites GPS (de acuerdo con la Relatividad), ¿cómo se explica que cada tipo de reloj se comporte de forma diferente? ¿con qué criterio se elige un determinado reloj para medir “correctamente” el tiempo, y se descartan los otros, si ni siquiera el reloj de cesio ha llegado a ser totalmente perfecto?
Saludos.