No sabemos de qué está hecho el espacio a nivel cuántico. Pero no importa, pues podemos describir dichos elementos de espacio y sus relaciones usando un grafo de espacios de Hilbert. El famoso Sean Carroll y su colega ChunJun Cao usan esta idea para ilustrar cómo podrían emerger algunas propiedades del espacio. Por desgracia todavía no han logrado que emerja el tiempo, ni el espaciotiempo descrito por la relatividad de Einstein.
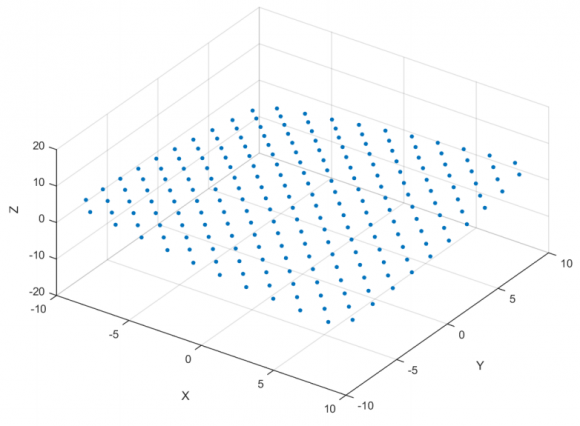
El espacio de Hilbert total (producto tensorial de todos los espacios de Hilbert de los elementos de espacio) para un espacio plano tiene dimensión finita y escala con el volumen; por tanto, su entropía escala con el área de su frontera, como predice la fórmula de Bekenstein y Hawking. La curvatura del espacio emerge del entrelazamiento de las perturbaciones locales en subgrafos; se puede interpretar como la aparición de un agujero de gusano que conecta dichas regiones del espacio, lo que sería una versión de la conjetura ER=EPR de Maldacena y Susskind.
La propuesta es muy sugerente, aunque se encuentre en una fase muy primitiva. Los físicos que lean esto disfrutarán leyendo el artículo de ChunJun Cao, Sean M. Carroll, «Space from Hilbert Space: Recovering Geometry from Bulk Entanglement,» Phys. Rev. D 95: 024031 (2017), doi: 10.1103/PhysRevD.95.024031, arXiv:1606.08444 [hep-th].
«It from bit» es la idea que subyace a la nueva propuesta de pregeometría cuántica de Cao y Carroll. El espacio sería pura información cuántica, una extensa red de paquetes discretos de información relacionados entre sí mediante la información mutua asociada a su entrelazamiento cuántico. Este tema está de moda en los últimos años en el marco de las ideas holográficas que usan las llamadas redes de tensores. Por ello la nueva propuesta recuerda a muchas otras de los últimos años. Aún así presenta algunos matices interesantes.
Me gustaría recordar a los profanos que en física cuántica lo habitual es cuantizar un sistema clásico. El proceso consiste en asociar a los estados del sistema clásico un espacio de Hilbert y a los observables clásicos operadores lineales en dicho espacio de Hilbert. Lo curioso es que hay sistemas clásicos muy diferentes entre sí que tras la cuantización conducen al mismo sistema cuántico. Por ejemplo, el genial Sidney Coleman descubrió que la cuantización de los bosones de la teoría clásica descrita por la ecuación del seno-Gordon en 1+1 dimensiones es equivalente a la cuantización de los fermiones de la teoría clásica de Thirring con masa; ambas teorías tienen el mismo espacio de Hilbert y existe una dualidad entre sus observables.
El proceso inverso a la cuantización es la construcción, a priori, de una teoría cuántica y luego estudiar sus posibles límites clásicos (en general, habrá infinitos límites). No conocemos la naturaleza física de los cuantos de espacio, luego no podemos describirlos por una teoría clásica que cuantizar. Sin embargo, podemos construir una teoría cuántica para dichos cuantos de espacio de tal forma que uno de sus límites clásicos sea el espacio. Este es el camino que proponen Cao y Carroll, aunque en su artículo aún está en fase muy provisional.
Te pongo un ejemplo bien conocido. Un cubit es un sistema cuántico descrito por el espacio de Hilbert de la esfera de Bloch. Todo sistema físico descrito (en cierto límite) por dicho espacio de Hilbert es una implementación física de un cubit. No importa si son dos niveles energéticos de un átomo, el espín de un electrón o la polarización de un fotón. Podemos estudiar las propiedades del cubit y el entrelazamiento entre cubits sin que nos importe su realización física.
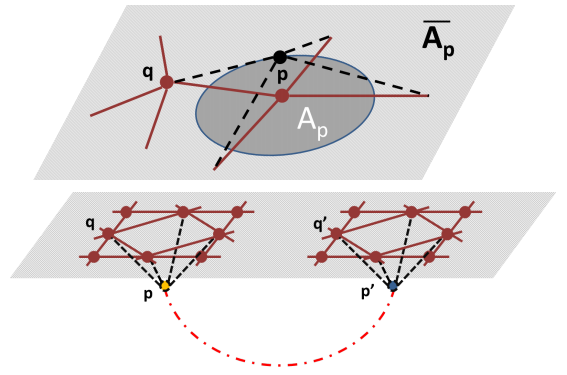
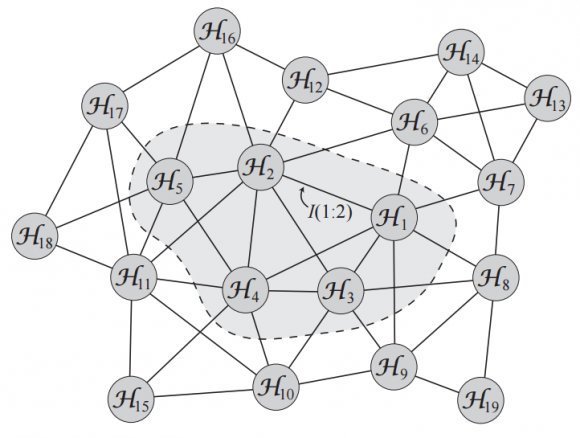
Cao y Carroll proponen que existe un espacio de Hilbert que se puede descomponer en un gran número de factores, cada uno un espacio de Hilbert de dimensión finita que describe un cuanto de espacio. Existe una entropía asociada a cada factor A, sea S(A). Los factores están conectados entre sí a pares (A,B) mediante su información mutua I(A:B) = S(A)+S(B)−S(AB). La información mutua actúa como métrica en el grafo que conecta todos los factores, lo que permite estudiar el límite continuo, que resulta en un espacio con geometría plana. Las perturbaciones de los estados cuánticos en cada factor, |ψ> → |ψ> + |δψ>, producen una curvatura local proporcional al cambio local de entropía. Estas perturbaciones se pueden entrelazar entre sí. En el límite continuo la teoría de campos descrita por este cambio de entropía debido a estos entrelazamientos implica una relación entre geometría y energía que recuerda a una versión clásica de las ecuaciones de Einstein. Gracias a ella se puede interpretar el entrelazamiento como asociado a regiones de gran curvatura, lo que recuerda a los agujeros de gusano de la conjetura ER=EPR.
Por supuesto, aunque las ideas de Cao y Carroll sean muy sugerentes, son muy generales, lo que les resta mucho valor. Lo más relevante es que se olvidan del tiempo, con lo que también se olvidan del espaciotiempo y, por tanto, su analogía con las ecuaciones de Einstein es bastante optimista. En este sentido, la gravedad entrópica de Erik Verlinde está mucho más cerca de las ecuaciones de Einstein que la nueva propuesta de Cao y Carroll.
En resumen, no quiero entrar en detalles técnicos, máxime cuando la mayoría de los cálculos son formales y su justificación es pobre. Cao y Carroll nos ofrecen el primer paso de lo que podría llevar a construir una teoría cuántica de la gravedad. Todavía no está clara la relación con otras propuestas similares, en estado más avanzado, como la gravedad cuántica de lazos (LQG), la quantum graphity de Smolin et al., o las ideas de grafos cuánticos aleatorios. Mucha gente le está dando vueltas a ideas que están muy relacionadas entre sí. Quizás alguien sea capaz de dar con la idea feliz que conecte todas estas ideas en un corpus de conocimiento que podamos llamar gravedad cuántica.


Todo este tema es fascinante.
Me pregunto si viviremos para ver el día en que pueda derivarse todo , de una teoría bien consistente.
¿La información mutua genera geometría?, me recuerda a Felix Klein aunque no podría afirmarlo.
Muy Genial el articulo.
Saludos
A mi estas noticias me parecen fascinantes, gracias Francis. Desde hace unos años han surgido atisbos que apuntan a una naturaleza del espacio tiempo muy distinta de la que percibimos. La implicación de la entropía y las teorías de la información, los artículos de Maldacena, el efecto holográfico, la posibilidad de que la estructura del espacio tiempo sea emergente a partir de efectos cuánticos… Me parece que estamos en un momento de la Física parecido a 1890, cuando a partir de varias pistas se barruntaba algo que, al final, se terminó aclarándose gracias a la RE, la RG y la MC, unas décadas después, logrando una avance formidable en la comprensión del Universo y dando un mazazo a la visión clásica del espacio y el tiempo.
Necesitamos un físico, que tenga una inspiración y visión como la de Albert Einstein o Max Planck, que sea capaz de interpretar todas las pistas dispersas que están apareciendo y las aglutine en una teoría coherente. Espero que eso suceda pronto, en una o dos décadas, para poder verlo.
Pero sea lo que sea, creo que será algo sorprendente, un nuevo golpe a la visión humana del Universo y la llave para entender la auténtica naturaleza del espacio-tiempo y su origen.
Aunque lo de Sean Carroll y compañía solo sea un mero borrador, es para valorarlo positivamente. Sobre todo teniendo en cuenta que este físico, Carroll, ha sido atacado de manera furibunda por el físico bloguero ultraderechista Lubos Motl, polemista incansable, que se ha cansado de llamarlo «crackpot» entre otras lindezas. Insultos que por cierto Lubos dedica a todo aquel que opina distinto a él. Pero ese es otro tema.
SalU2
Pobre Molt, un físico que no se ha enterado de que la física es el teorema de Noether……………y otros flecos. Debe de joderle que una mujer le haya birlado los cromos, o las cuerdas, o el sentido común.
Que se dedique a generalizarlo ………………para flecos
Por lo demás, gracias Francis.
Tal como bien dice Francis, esta idea es parte de un cúmulo de pensamientos (¿superficialmente?) relacionacionados entre sí.
1) Algo curioso es que en variantes de estas discusiones se suele sacar a colación cierta asimetría entre espacio y tiempo emergente. Yo sé que suena a primera vista a no haber aprendido la lección de la relatividad especial que versa de la unidad del espaciotiempo, pero realmente es así.
Ads/Cft aparenta ser un ejemplo de física en donde una dimensión(puramente) espacial parece emerger, bien es cierto que Ads es un fondo muy simétrico, pero hace poco atendí un seminario en donde se hablaba de tiempo emergente en la teoría de Bagger Lambert sobre stacks de M5 branas. Algo escuché también sobre que en la dualidad ds/cft puede pasar lo mismo (aquí puedo estar hablando con descuido).
El propio Caroll ha dicho que bien el espacio puede ser emergente y el tiempo fundamental e irreducible.
Este paper es extremadamente profundo, habla sobre espaciotiempo emergente, esta asimetría y su autor es Nathan Seiberg https://arxiv.org/abs/hep-th/0601234
2) Molt tiene un buen punto en atacar a las personas que han pensado en triangulaciones dinámicas causales, graficidad cuántica, LQG, tensor networks e incluso el cálculo de Regge… No hay estructuras discretas que tengan ni la mitad de sofisticación, propiedades y posibilidades que otras geometrías continuas, siempre las geometrías discretas sirven para aproximar las propiedades de un continuo nunca son intrínsecamente más «divertidas por sí mismas» (Aquí me fascinaria que alguien me corrigiese), los topólogos saben que no cualquier variedad es triagulable, no cualquier espacio es «aproximable» (No todo espacio es un CW complejo)… es más… el análisis es muy pobre en espacios discretos (ojo en los p-ádicos es interesantísimo pero una topología totalmente disconexa no es un espacio discreto).
En cambio en teoría M es muy interesante la aparición de las curvas elípticas, su relación con formas modulares, hay superficies de Riemann. T dualidad es una forma exótica de introducir una escala mínima de distancia sin discretizar (yo sé que a Lubos le patea que se diga esto), Mirror Symmetry…
En clase estamos estudiando que una teoría de cuerdas compactificada y en presencia de flujos sobre la variedad de compactificación requiere una nueva disciplina llamada «Geometría generalizada» pues la propia estructura compleja de la calabi yau fluctúa y su teoría de deformaciones admite «salirse» de la categoría de variedades complejas…
Que emocionante es imaginarse lo mucho que cambiarán (esperemos) nuestras nociones de espaciotiempo a finales de siglo (por ejemplo).
Sobre el paper de Carroll:
Algo negativo es que a priori el paper es lo que bien apunta Francis sobre el límite clásico… Incluso en este límite hace falta mucho más para deducir la teoría de Einstein y tener algo como un agujero negro, lo curioso es que como se señala en la entrada la idea ER=EPR puede ayudar a definir vía el entrelazamiento gravedad (al menos de manera dual como se hace en el paper de Maldacena y Susskind) y ciertamente si imponemos una cota máxima a la complejidad de un proceso entonces hay algo como un agujero negro (región de máxima curvatura), de esto ha hablado Susskind en sus trabajos con Harlow y es muy sugerente como estas ideas también parecen estar relacionadas entre sí.
Recientemente se me ha estado creando un confusión con la palabra «emerger» en estos contextos. Aun no entiendo bien porque se sigue usando.
Cuando algo parece emerger me hacen pensar como que se le quita «física» o cierta causalidad a los sistemas dinámicos.
Digamos que yo programo en C++ y OpenGL una escena y su física asociada en tres dimensiones. Uso todo el formalismo del calculo vectorial implementado como funciones de C++.
En este contexto existe ciertamente, una realidad tridimensional no emergente, sino más bien definida por el conjunto de reglas algoritmicas (leyes físicas escritas como funciones de C++).
En este nivel nadie discute nada y todo parece claro. Pero bajemos un poco más y lleguemos al nivel binario, incluso a la electrónica implicada. Es decir, cuando yo llevo mis .cpp a .exe por medio de compilación en x86 ó 64, en este nivel tengo toda una electrodinámica asociada a la dinámica mutua que existe entre el procesador, memoria y video en una arquitectura x86 o 64. Desde el punto de vista del escenario tridimensional dicha realidad emerge de esta electrodinámica, ya que tiende a ser más caótica. En un nivel intermedio podríamos tener toda la fenomenología de cierta máquina de turing, pero esto depende del nivel en que nos encontremos.
Otro ejemplo más reciente.
La inteligencia de AlphaGo emerge de forma no conocida a partir de sus redes neuronales. Una vez entrenada, nadie sabe como funciona pero lo hace.
Este «emerger» de inteligencia no se podría aplicar en el caso de superordenadores jugando al ajedréz, cuyo funcionamiento, hasta donde tengo entendido, es más predecible y depende más de la fuerza bruta aplicada a una serie de jugadas previamente almacenadas y/o consultadas en una base de datos.
Mi «creencia religiosa» es que en el caso de AlphaGo debe existir cierta algoritmia en ese «emerger», ya que a la final se toman deciciones discretas, la cuestion es que son muy difíciles de reconocer. Y para el caso contrario, el caso del ajedréz, sólo habría que considerar toda la electrodinámica de un superordenador para poder decir que la realidad subjetiva al juego de ajadrez (posibles estados del sistema de piezas+posiciones, conjunto de reglas, etc) emerge de un comportamiento más caótico y microscópico en el nivel de los átomos.
Y bueno, ese es el rollo que tengo con la palabra «emerger», me parece subjetiva y es relativa al nivel en que te encuentres.