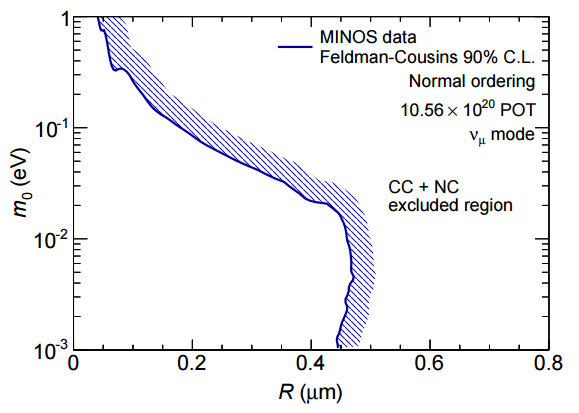
El tamaño de las dimensiones extra gigantes del espaciotiempo se puede estimar de muchas formas. El detector de neutrinos MINOS del Fermilab restringe su tamaño a menos de 0,45 μm al 90% C.L. al descartar la existencia de neutrinos estériles. Para ello se interpretan estos hipotéticos neutrinos como estados de Kaluza–Klein asociados a las dimensiones extra del espaciotiempo.
MINOS ha observado entre 2005 y 2012 los neutrinos producidos por la colisión de 10,56×1020 protones contra un blanco de grafito gracias al haz NuMI del Fermilab. MINOS aventaja a otros detectores de neutrinos en este tipo de búsqueda porque tiene dos detectores, el cercano (Near) y el lejano (Far), que permiten estudiar desviaciones en el proceso de oscilación de los neutrinos que podrían ser debidas a la existencia de neutrinos estériles.
El artículo es The MINOS Collaboration, «Constraints on Large Extra Dimensions from the MINOS Experiment,» arXiv:1608.06964 [hep-ex]. El mejor límite para la masa de los neutrinos es de KamLAND-Zen Collaboration, «Search for Majorana Neutrinos near the Inverted Mass Hierarchy Region with KamLAND-Zen,» Phys. Rev. Lett. 117: 082503 (2016), doi: 10.1103/PhysRevLett.117.082503, arXiv:1605.02889 [hep-ex].
La compactificación en forma de cilindro de las dimensiones extra del espaciotiempo permite que los campos cuánticos asociados a las partículas tengan excitaciones que den una o varias vueltas completas al cilindro. Las partículas conocidas corresponden al estado fundamental, cuando no se da ninguna vuelta (no winding). Se llama estados de Kaluza–Klein a los estados de las partículas del campo cuando este da una o varias vueltas. Si existen las dimensiones extra gigantes (nombre asociado a las que tienen un radio superior al nanómetro), todas las partículas deben tener estados de Kaluza–Klein asociados. Por tanto, si no se observan estos estados podemos acotar el tamaño de las dimensiones extra (la cota depende de su número y las mejores cotas se obtienen para una sola dimensión extra).
Sabemos que hay neutrinos de tres sabores (o familias), llamados νe, νµ, y ντ. Igual que ocurre con los quarks, los neutrinos con masa, llamados ν1, ν2, ν3, son estados mezcla de los estados con sabor bien definido. Pero a diferencia de los quarks, los neutrinos se pueden observar como partículas libres, lo que permite estudiar esta mezcla. La llamada oscilación de los neutrinos (como la mezcla de los quarks) está parametrizada por tres ángulos de mezcla θ12, θ13, y θ23. Además, hay ángulos de fase asociados a la violación de la simetría CP; si los neutrinos son partículas de Dirac, como los quarks, hay un solo ángulo de fase δCP; pero si los neutrinos fueran partículas de Majorana, habría tres ángulos de fase, llamados δCP, α1, y α2. Aún no sabemos si los neutrinos son partículas de Dirac o de Majorana, aunque este último caso es el preferido por la mayoría de los físicos de partículas.
El haz de neutrinos NuMI produce neutrinos muónicos. Su número se reduce conforme se propagan en dirección a los dos detectores de MINOS. Si existieran los neutrinos estériles (νs), parte de los neutrinos muónicos oscilarían a ellos, νµ → νs. La probabilidad de esta oscilación crece si además existen dimensiones extra del espaciotiempo y los neutrinos estériles tienen estados de Kaluza–Klein. De hecho, esta posibilidad permite explicar por qué los neutrinos de Dirac tienen una masa tan pequeña (Nima Arkani-Hamed, Savas Dimopoulos, …, John March-Russell, «Neutrino Masses from Large Extra Dimensions,» Phys. Rev. D 65: 024032 (2002), doi: 10.1103/PhysRevD.65.024032, arXiv:hep-ph/9811448).
Gracias a la gran precisión de los detectores de MINOS se pueden buscar los neutrinos estériles. Y su búsqueda permite acotar el tamaño de las dimensiones extra del espaciotiempo (3+1+d, con d ≥ 2 dimensiones compactificadas). Para simplificar el análisis se asume que una de las dimensiones extra es mucho mayor que las demás y está compactificada en una circunferencia de radio R. El cálculo de las probabilidades de oscilación, P(νµ→νµ) y P(νµ→νs), depende de R. El estudio experimental de sus valores permite, por tanto, acotar el valor del radio R. Como los hipotéticos neutrinos estériles no han sido observados, sólo se puede obtener una cota superior para dicho radio, que dependerá de la masa del neutrino más masivo.
Los límites cosmológicos para la masa de los neutrinos indican que su masa es inferior a unos 0,2 eV = 200 meV. El último límite no cosmológico ha sido publicado por el experimento KamLAND-Zen. Estudia la desintegración beta doble sin neutrinos (0νββ) en átomos de 136Xe. Aún no ha sido observada, luego se ha obtenido un límite superior para su vida media, en concreto, es mayor de 1,07 × 1026 años al 90% C.L. Este valor permite estimar la masa de los neutrinos (si son de Majorana, para que se dé la 0νββ) entre 61 y 165 meV (el rango es amplio porque depende de cómo se estimen los elementos de la matriz nuclear de desintegración).
Por tanto, si la masa del neutrino más masivo es menor de 100 meV = 0,1 eV, entonces el tamaño de la dimensión extra del espaciotiempo más grande es menor de 0,45 μm al 90% C.L. Este tamaño es el mejor obtenido en experimentos con neutrinos y su valor es comparable al obtenido con experimentos que estudian la gravedad a distancias cortas.