Varios matemáticos han obtenido el premio Nobel, incluido el español José Echegaray (1832–1916) que obtuvo el Premio Nobel de Literatura en 1904. El más famoso es John Forbes Nash Jr. (1928–2015), por escribir en 1950 un artículo de una sola página, aunque apareció en dos páginas consecutivas, en la revista PNAS. Gracias a una sola página de matemáticas logró el Premio Nobel de Economía en 1994. ¡Una sola página!
El artículo era el resumen de su tesis doctoral, dirigida por Albert W. Tucker, de solo 32 páginas. El artículo en cuestión es John F. Nash, Jr., «Equilibrium points in n-person games,» Proceedings National Academy of Sciences 36: 48–49 (1950), doi: 10.1073/pnas.36.1.48 [PDF]. Su tesis doctoral es «Non-cooperative games,» Ph.D. thesis, Mathematics Department, Princeton University, 1950 [PDF]. Sobre teoría de juegos publicó otros tres artículos (también mencionados por el Comité Nobel): «The bargaining problem,» Econometrica 18: 155–162 (1950), doi: 10.2307/1907266 [PDF], «Non-cooperative games,» Annals of Mathematics 54: 286–295 (1951), doi: 10.2307/1969529 [PDF], y «Two-person cooperative games,» Econometrica 21: 128–140 (1953), doi: 10.2307/1906951 [PDF].
Me lo ha recordado César Tomé, «Cuatro páginas para un nobel,» Cuaderno de Cultura Científica, 11 Oct 2016. Te recomiendo en este blog «Descanse en paz el genial matemático John F. Nash, Jr.,» LCMF, 24 May 2015, y «José Echegaray y lo que tiene hacer un matemático español para ganar el Premio Nobel,» LCMF, 19 Abr 2011.
Por cierto, esta entrada participa en la Edición 7.7 del Carnaval de Matemáticas, que en esta ocasión organiza Los Matemáticos no son gente seria, el blog de Juan Martínez-Tébar Giménez (Albacete). Te animo desde aquí a participar en el Carnaval entre el 30 de octubre y el 6 de noviembre.
La verdad, no me apetece contarte qué es la teoría de juegos, qué son los puntos de equilibrio de Nash, o por qué fueron tan relevantes en Economía. Yo he impartido conferencias divulgativas sobre el tema y si te interesa el tema te recomiendo consultar las muchas fuentes que hay en la web.
Tampoco te quiero hablar de la película «A Beautiful Mind» (2001), en España «Una mente maravillosa», que ganó el Óscar a la mejor película (aunque su protagonista, Russell Crowe, se quedó sin el codiciado galardón). Ni de la biografía de Sylvia Nasar en la que está basada, aunque su contenido sea bastante más escabroso (ya se sabe que el cine de Hollywood debe ser políticamente correcto).
Hoy te voy a hablar de una aplicación curiosa de la teoría de juegos, estudiar cómo toman decisiones los jugadores de fútbol. El caso más estudiado es el lanzamiento de penaltis. Quizás pienses que es algo poco matemático usar el fútbol para hablar de teoría de juegos, por ello me haré eco del trabajo fin de grado de Ana González Tejerina, «Teoría de Juegos y Fútbol Femenino,» tutorizado por Pedro Rey-Biel, Universitat Autònoma de Barcelona (Jun. 2016) [UAB CAT], que está inspirado en el libro de Ignacio Palacios-Huerta, «Beautiful Game Theory: How Soccer Can Help Economics,» Princeton University Press (Jun. 2014). Por cierto, como puedes imaginar, Ana es jugadora de fútbol, desde los 13 años en el Molins de Rei C.F. y luego fichó por el Club de Fútbol Sant Andreu de la Barca Agrupació (CF SABA).
El fútbol es un juego de suma cero. La tanda de penaltis parece una lotería, pero no lo es. El estudio de Palacios-Huerta en 2010 demostró que “la moneda también juega” (al decidir por sorteo quién empieza lanzando); el equipo que lanza el primer penalti tiene casi un 61% de probabilidades de ganar el partido, contra el 39% del equipo que lanza el segundo. La teoría de juegos también permite aconsejar a los jugadores y a los porteros qué hacer en una tanda de penaltis.
La teoría de Nash predice que los jugadores suelen lanzar los penaltis de forma aleatoria e impredecible y en las proporciones ideales. Palacios-Huerta (2014) analizó 9017 penaltis en partidos de fútbol profesional y encontró que los jugadores prefieren lanzar un penalti hacia su «lado natural», la derecha si son diestros y la izquierda si son zurdos. Por ejemplo, el 60% de los lanzamientos de los jugadores diestros fueron a la derecha de la red, y solo el 40% fueron a la izquierda.
Por cierto, nos cuenta Ana que Ignacio Palacios-Huerta fue fichado por el Chelsea F.C. en 2008 para la final de la UEFA Champions League; también fue contratado por Holanda en el Mundial de 2010 para enfrentarse en la final a España y por el Athletic Club de Bilbao en 2011.
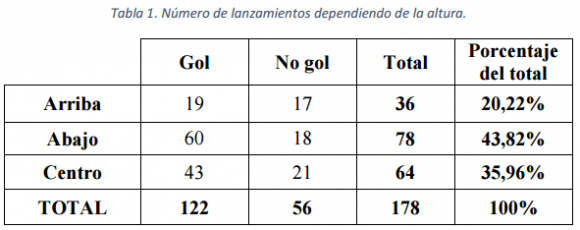
El estudio de campo de Ana se basó en 178 penaltis lanzados por 89 jugadoras diferentes de 8 equipos. Se llevaron a cabo la semana del 18 al 22 de enero de 2016. Se han estudiado doce hipótesis, todas muy interesantes. Yo solo destacaré unas pocas (los interesados en las demás pueden consultar el trabajo fin de grado de Ana).
¿Hay más probabilidades de marcar gol lanzando el penalti hacia abajo que no hacia arriba o hacia el centro? ¿Hay más probabilidades de marcar gol lanzando el penalti hacia uno de los lados que no hacia el centro? Sí, así es, la forma más efectiva de lanzar un penalti es lanzando hacia abajo y hacia un lado. Las jugadoras conseguían un 15% más de efectividad lanzando por abajo y no por arriba o por el centro, y un 35% más de efectividad al lanzar el penalti por un lado de la portería.
¿Las jugadoras tienden a lanzar hacia su lado natural? A diferencia de lo que observó Palacios-Huerta, el estudio de Ana indica que las jugadoras no tienden a lanzar hacia su lado natural en los lanzamientos de penaltis. Las zurdas tienden a lanzar hacia la derecha en un 60% de las ocasiones, mientras que las diestras lo hacen en poco más del 40% de las veces. Además, a la hora de lanzar hacia la izquierda de la portera, son las jugadoras diestras las que lo hacen en mayor medida, siendo de casi el 50% de las veces, mientras que apenas superan el 10% los lanzamientos de jugadoras zurdas que lanzan hacia este lado.
Las jugadoras tienden a lanzar hacia su lado menos natural sin importar su nivel de aversión al riesgo. La razón parece ser que las jugadoras chuten con el interior del pie, y no con el empeine. Con el empeine se consigue más fuerza, pero es más difícil de controlar la dirección, mientras que con el empeine es más fácil tirar hacia donde queremos que vaya el balón y es más fácil lanzar el penalti hacia el lado no natural.
En resumen, un trabajo muy curioso e interesante, que muestra la teoría de juegos y el análisis estadístico de datos en acción. Una página llevó a un nobel y dicho nobel nos llevó al fútbol femenino. Las matemáticas siempre nos llevan por caminos insondables. Así son de sugerentes.
Y, por cierto, François Englert y Peter Higgs obtuvieron el premio Nobel de Física en 2013 por tres artículos publicados en 1964 que totalizan cinco páginas y media, mal contadas. Pero eso sería tema para una participación en el ya extinto Carnaval de Física.







Siempre interesante leer acerca de Nash y lo relacionado con a Teoría de Juegos. Gracias por esta entrada.
Por cierto, Francis: ¿hubieras incluido el Nobel de Economía en una hipotética entrada «Los Premios Nobel de Ciencias de 1994»?
Saludos
Víctor, ¿escrita en 1994? No lo sé, supongo que no.
Siempre he sido aficionado a la física y las matemáticas, y cada vez más, estoy descubriendo tus artículos y son maravillosos.
He entrado porque siempre he sido fan de John Nash.
Cada vez estoy más motivado para estudiar y una de las razones es que menciones a Echegaray el cuál estudió en el instituto en el que yo entro este año a cursar Bachiller.
Un saludo.