El ruido es el gran problema de los ordenadores cuánticos. Una copa llena por la mitad puede parecer medio lleno o medio vacía. Un optimista afirmará que las técnicas cuánticas de corrección de errores lidiarán con el problema del ruido. Por contra, un pesimista opinará que el ruido cuántico siempre será imposible de evitar. Esta figura ilustra la hipótesis optimista. Los algoritmos clásicos tolerantes a fallos se podrán extender al mundo cuántico gracias a técnicas cuánticas de corrección de errores. Gracias a ellos se espera algún día haya algoritmos cuánticos que manejen de forma robusta la información cuántica.
Hay físicos cuánticos que se declaran pesimistas. Un ejemplo es Gil Kalai en «The Quantum Computer Puzzle,» Notices of the AMS 63: 508-516 (May 2016), doi: 10.1090/noti1380; este artículo se basa en dos previos, Gil Kalai, «How Quantum Computers Fail: Quantum Codes, Correlations in Physical Systems, and Noise Accumulation,» arXiv:1106.0485 [quant-ph], y Gil Kalai, Guy Kindler, «Gaussian Noise Sensitivity and BosonSampling,» arXiv:1409.3093 [quant-ph]. Por cierto, ambos dibujos son de Neta Kalai.
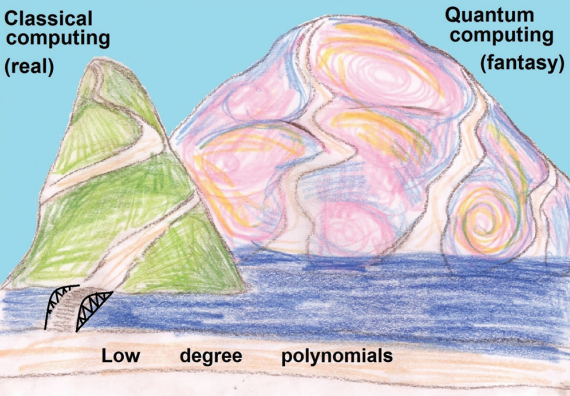
Esta figura ilustra la hipótesis pesimista. La brecha computacional que supone el ruido cuántico es tan grande que nunca podrá ser superada con algoritmos eficientes. Como un río demasiado ancho para ser cruzado de forma eficiente, sólo podremos cruzarlo hasta el mundo clásico, permaneciendo como pura fantasía la posibilidad de cruzarlo hasta el mundo cuántico.
Se llama supremacía cuántica a la demostración de un ordenador cuántico más rápido que uno clásico en la implementación física de la solución a un problema concreto. No más rápido en teoría. Más rápido a la hora de la verdad. Los optimistas piensan que la supremacía cuántica está a la vuelta de la esquina (antes de 2050). Los pesimistas opinan que nunca será alcanzada, pues al crecer el número de estados de un sistema cuántico no trivial se comportará como clásico. Su indicio más firme es que no observamos ordenadores cuánticos en la Naturaleza que nos puedan inspirar.
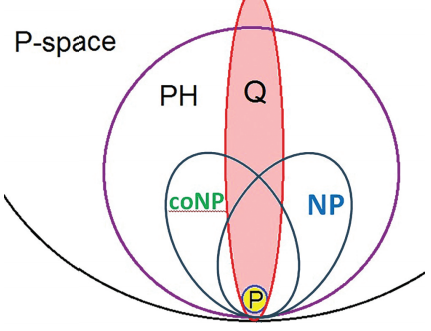
En la teoría de la complejidad computacional un algoritmo (clásico) es eficiente si está en la clase P, es decir, si se puede ejecutar usando un número polinómico de pasos en función del tamaño de la entrada. La clase Q de algoritmos cuánticos eficientes parece ser mayor que P, pues la factorización de números primos y unos pocos problemas más están en Q, pero no sabemos si están en P (la conjetura P ≠ NP sugiere que no lo están).
La supremacía cuántica es imposible si la tolerancia cuántica a fallos no es viable en computación cuántica. Los algoritmos de corrección de errores son muy útiles, pero no sabemos cómo escala su versión óptima. Si escalan de forma lineal con el número de cubits, nos encontraremos ante el muro de la hipótesis pesimista. Para resolver un problema que requiere O(N) cubits de cómputo necesitaríamos O(N) cubits de corrección de errores. Un número excesivo fuera de toda duda. Debe escalar de forma sublineal si queremos observar algún día la tan deseada supremacía cuántica.
El ruido cuántico y la tolerancia a fallos son las claves para decidir entre la hipotesis optimista y la pesimista. A largo plazo no sabemos la que prevalecerá. Kalai, ahora mismo, se decanta por la pesimista.



Hola profesor Francis
Soy matemático y me gustaría poder estudiar por mi cuenta computación cuántica y complejidad computacional. ¿Tienes alguna sugerencia de literatura por la que pueda empezar?
Muchas gracias por las entradas tan extraordinarias que publicas.
Saludos
Perdón por responder una pregunta que no iba dirigida a mí, pero no puedo resistirme a recomendar este libro:
https://www.amazon.co.uk/Quantum-Computation-Information-10th-Anniversary/dp/1107002176
Incluye una introducción a la física cuántica y otra a la teoría de la computación que son una maravilla, además de información actualizada sobre computación cuántica.
Un saludo.
Gracias, Daniel, el libro de Nielsen-Chuang es muy bueno.
Gracias Daniel y Francis por la sugerencia.
Saludos
Excelente explicacion del problema del ruido cuantico incluso para simples aficionados sin estudios de fisica o matematicas como yo. Gracias.
Vsego
No tiene importancia, pero yo no diría que Gil Kalai es un físico cuántico. Si es el mismo que creo, se trata de un matemático que se ha dedicado a la combinatoria fundamentalmente. No sabía que también se dedicaba a elucubraciones cuánticas.
Francis
Que piensas de este trabajo https://arxiv.org/abs/1603.03384
Caroline, se trata de un trabajo interesante (la tecnología de iones atrapados es una de las más prometedoras en computación cuántica y es la que, de tener éxito, le dará el Nobel a un español, Cirac). Sin embargo, solo usan dos cubits y son de fidelidad baja (0,985), cuando los cubits de diamante (estado sólido) alcanzan fidelidades superiores a 0,99995. Los autores opinan que su idea es escalable (en teoría), pero no lo demuestran (en la práctica).
¿Cuándo tendrán un sistema con 16 cubits? Aunque los autores imaginen en su artículo un sistema con millones de cubits usando su nueva tecnología, yo prefiero tener los pies sobre la tierra. Hasta que no tengan un sistema con 16 cubits tendré enormes dudas sobre su escalabilidad (auguro que les va a costar mucho trabajo lograrlo). Espero equivocarme. Crucemos los dedos.
Me gustaría que me recomendaseis algún libro bueno de computación cuántica, que no sea rollero ni con demasiado formalismo matemático, que mezcle teoría, detalles sobre la construcción experimental y detalles sobre los algoritmos, que incorpore temas novedosos.
Algo que aunque haga pudiera hacer un breve repaso de MC se centre en su apliación a la computación cuántica. Para alguien con conocimientos básicos de computación clásica y que sacó notable en el examen de mecánica cuántica pero ya hace muchos años.
He creado una lista de candidatos a partir de críticas que he visto en Amazon, el problema es que no comparan unos con otros.
A Short Introduction to Quantum Information and Quantum Computation, Le Bellac, 2006
An Introduction to Quantum Computing Algorithms, Pittenger, 2001
An introduction to quantum computing, Kaye, Laflamme,Mosca, 2007
Classical and Quantum Computation, Kitaev, 2002
Elements of quantum computation and Quantum Communication, Anirban, 2013.
Entanglement, quantum phase transitions and quantum algorithms, Lacort,
Experimental Aspects of Quantum Computing, Everitt, 2005
Explorations in Quantum Computing, Williams, 2010
Introduction to Quantum Information Processing, Lucke.
Introduction to Information Retrieval and Quantum Mechanics, Melucci, 2015
Introduction to Quantum Computing, Wartrous Notes, 2006
Logic and Algebraic Structures in Quantum Computing, Chubb, 2010
Nano, Quantum And Molecular Computing, Shukla, Bahar, 2004
Quantum Algorithms Via Linear Algebra, Lipton, 2014
Quantum Computation and Quantum Communication, Theory and Experiments, Pavicic, 2006
Quantum Computation and Quantum Information, Nielsen, Chuang, 2011
Quantum Information and Quantum Computing, Nakahara, 2013
Quantum Computer Science An Introduction, Mermin, 2007
Quantum Computer Science, Lanzagorta, Uhlmann, 2008
Quantum Computer. How It Works Issue 95, 2017
Quantum Computing, A Gentle Introduction, Rieffel, Polak, 2014
Quantum Computing Explained, McMahon, 2007
Quantum Computing for Computer Architects, Metodi, 2011
Quantum Computing for computer scientists, Yanofsky y Manucci, 2008
Quantum Computing since Democritus, Aaronson, 2013
Quantum Engineering, Zagonskin, 2011
Quantum Information Computation and Communication, Jones, 2010
Quantum Quenching, Annealing and Computation, Somma, 2010
Quantum Walks and Search Algorithms, Portugal, 2013
Quantum computation, Aharanov,
Quantum Walks for Computer Scientists, Venegas, 2008
Reversible Computing Fundamentals, Quantum Computing, and Applications, De Vos, 2010
The Temple of Quantum Computing, Perry, 2004.
The Limits of Quantum Computers, Aaronson
What Quantum Computing Means to Data Mining, Wittek, 2014
¿Habéis leído alguno?. ¿Incluirías alguno más , tal vez alguno de Teoría de la información cuántica?
¿Qué ranking haríais? o al menos decir cuál no vale la pena leerlo o cuál os parece bueno?
Algunas personas eligen los de Laflamme, Rieffel o Yanofsky como libros introductorios. Supongo que porque serán buenos, pero hay muchos libros que son menos votados simplemente porque nuevos y desconocidos.
Y eligen Nielsen como el avanzado. ¿Qué alternativa hay?