Como todos los años, os presento las transparencias y una transcripción (con añadidos y comentarios) de mi charla Naukas Bilbao 2017 [video]. Titulada «El espín para irreductibles», con una duración de 10 minutos, tenía como objetivo que Javier Peláez, alias @Irreductible, aprendiera cómo explicarle el espín a un público general usando una metáfora sencilla. En concreto la llamada metáfora del sacacorchos, también conocida entre los físicos como metáfora del momento angular orbital; el famoso divulgador Dr. Quantum (Fred A. Wolf) le llama metáfora del poste de barbería.
Yo esperaba que esta metáfora ayudara a mucha gente a entender el espín, uno de los conceptos cuánticos más complicados de comprender, según dicen algunos. Sin embargo, tras mi charla, solo algunos físicos e ingenieros de telecomunicaciones en el Euskalduna afirmaron haber entendido mi argumento. Parece ser que solo comprendieron mi metáfora quienes tienen una idea clara de lo que es una onda. Yo pensaba que el concepto de pseudoespín, que aparece en el electromagnetismo clásico, era una analogía ideal podía acercar el espín cuántico a un público lego cuya intuición es clásica. Por lo que observé tras mi charla, estaba equivocado.
Como suele ocurrir con muchas metáforas, en lugar de ayudar a entender generan más confusión. Gran parte del público fue incapaz de entender la metáfora del sacacorchos; me parecía que todo el mundo podría imaginar un movimiento en espiral acoplado a un movimiento oscilatorio, sin embargo, quizás mi imaginación geométrica está más educada que la del público profano. En retrospectiva creo que debería haber dedicado toda mi charla al contenido de una sola de las transparencias y haber dejado el resto para el blog. Aún así, me alegró mucho que una de las estrellas de Naukas Bilbao 2017 haya sido el espín; muchas charlas, incluso en otros eventos de Bizkaia Zientzia Plaza, mencionaron el espín. Si mi charla ha motivado a algunos jóvenes a profundizar en este concepto, mi misión ha sido un éxito, aunque no haya alcanzado su gran objetivo inicial.

Te recomiendo disfrutar del vídeo de la charla en la web de EITB Kosmos.
Mi charla de 10 minutos está basada en la charla de 60 minutos de Richard P. Feynman, «Elementary Particles and the Laws of Physics,» (1986), video youtube; te la recomiendo de forma encarecida, aunque esté en inglés y la calidad del vídeo sea tan mala que no se ven las transparencias en acetato; por fortuna, tienes una transcripción, con figuras y fórmulas en el libro Richard P. Feynman, Steven Weinberg, «Elementary Particles and the Laws of Physics: The 1986 Dirac Memorial Lectures,» (1987) [amazon]. Siendo difícil de entender, tienes una explicación asequible en los capítulos 2–10 del libro de Fred A. Wolf (Dr. Quantum), «Bucles temporales y pliegues espaciales», Obelisco (2013) [amazon], pero, por favor, no leas ni el capítulo 1 ni el 11, que son pseudocientíficos.
Para los físicos interesados, la fuente principal de este charla es el muy recomendable libro de Ian Duck, E.C.G. Sudarshan, «Pauli And The Spin-Statistics Theorem,» Scientific World (1998) [amazon]. Quienes estén interesados en la metáfora del momento angular orbital disfrutarán con el primero de los artículos del libro editado por David L. Andrews, Mohamed Babiker, «The Angular Momentum of Light 1st Edition,» CUP (2013) [amazon]. Hay cientos de artículos en la web sobre este tema, he consultado decenas, así que animo a buscar más información si estos libros os dejan insatisfechos.
Por cierto, el título «el espín para irreductibles» era un juego de palabras con el alias de Javier Peláez, Irreductible, y con las representaciones irreducibles de álgebras de Lie; mi idea antes del verano era explicar por qué la masa y el espín son los casimires asociados a las representaciones irreducibles del grupo de Poincaré. Tras el verano decidí que explicar estos conceptos a legos requiere una charla de más de diez minutos; quizás me equivoqué, pero se me ocurrí la idea de usar el pseudoespín y el momento angular orbital en lugar de la teoría de representaciones. Quizás metí la pata, vista la respuesta del público durante el evento. La divulgación requiere tomar decisiones y no siempre resultan acertadas.
Javier Peláez, alias @Irreductible, se preguntaba en Naukas: “¿Alguien llega a comprender realmente qué es el espín?” Y afirmaba que jamás entendería que “el espín es una propiedad cuántica que describe un momento angular intrínseco de una partícula».
¿Qué es el momento angular? La matemática Emmy Noether nos enseñó que el momento angular es la magnitud física que se conserva en un sistema físico que sea invariante ante rotaciones respecto a cierto eje de giro. El momento angular tiene un signo que depende de sentido de giro del sistema.
Noether demostró que toda simetría de un sistema físico tiene asociada una magnitud física que se conserva. La energía se conserva si un sistema físico es invariante ante traslaciones en el tiempo; si un experimento realizado hoy o realizado mañana da los mismos resultados. El momento lineal, o cantidad de movimiento, el producto de la masa por la velocidad, se conserva si un sistema físico es invariante ante traslaciones en el espacio; si un experimento realizado en Bilbao o realizado en Málaga da los mismos resultados. El momento angular, el producto vectorial del radio vector de giro y el momento lineal, se conserva si un sistema físico es invariante ante rotaciones; si al rotar un experimento no cambian sus resultados.
La constante de Planck tiene unidades de momento angular y se puede interpretar como la mínima cantidad en la que puede cambiar el momento angular de un sistema físico. La proyección del momento angular sobre el eje de giro esta cuantizada y sus valores solo pueden aumentar o decrecer en unidades de la constante de Planck. Por ello, el valor máximo de la proyección del momento angular sobre el eje de giro solo puede ser un múltiplo entero o semientero de la constante de Planck. Si es un múltiplo entero tendrá un número impar de valores, por ejemplo, cinco valores (+2, +1, 0, −1, −2), tres valores (+1, 0, −1), o un valor (0); si es un múltiplo semientero tendrá un número par de valores, por ejemplo, dos valores (+1/2 y −1/2), o cuatro valores (+3/2, +1/2, −1/2, −3/2).
El principio de indeterminación de Heisenberg entre la posición y el momento lineal implica que no podemos determinar de forma simultánea ambas magnitudes, . El momento angular es el producto de la posición por el momento lineal,
, por lo que no podemos determinar las tres componentes del momento angular de forma simultánea, por ejemplo,
. Por fortuna, podemos determinar con exactitud su módulo,
, y una de sus componentes, la proyectada sobre el eje de giro, sea
.
Un cálculo sencillo demuestra que el módulo del momento angular es proporcional a la constante de Planck, , siendo los valores de su proyección sobre el eje de giro son múltiplos de la constante de Planck,
, o bien múltiplos enteros
, o bien múltiplos semienteros
. El número de valores del momento angular proyectado
es
. Repito lo dicho antes, si
, entonces la proyección sobre el eje toma los cinco valores (+2, +1, 0, −1, −2), si es
toma los tres valores (+1, 0, −1), o si es
un único valor (0); si es un múltiplo semientero tendrá un número par de valores, por ejemplo, si
tomará dos valores (+1/2 y −1/2), o si es $latex \ell=3/2$ cuatro valores (+3/2, +1/2, −1/2, −3/2).
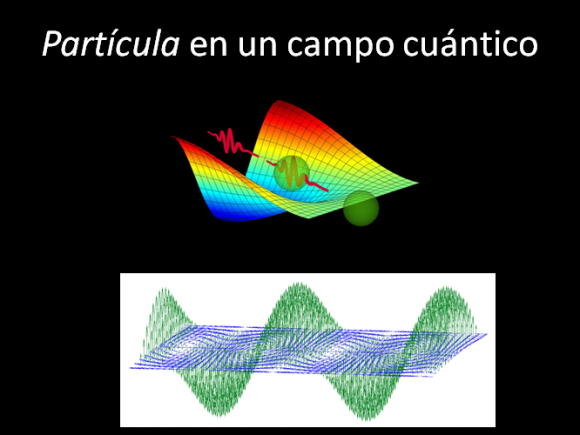
¿Qué es una partícula? Una partícula es una excitación, una vibración, una onda, un cuanto de un campo cuántico. Una partícula ocupa cierta región del espaciotiempo, dada por su longitud de onda de De Broglie. Una partícula es cuántica por dos motivos, su número está cuantizado y su momento angular intrínseco también. En una región del espaciotiempo el número de partículas está cuantizado, puede haber una partícula, o dos, o tres, pero no puede haber una fracción de partícula. La partícula tiene energía, momento lineal (o cantidad de movimiento) y momento angular, propiedades que puede transferir de unas regiones del espaciotiempo a otras. Además, su momento angular intrínseco también está cuantizado (como todo momento angular de un sistema cuántico).
Una onda móvil es una oscilación con crestas y valles. La partícula es una vibración cuantizada en el espacio y el tiempo del campo cuántico; esta onda se puede descomponer en dos componentes, una asociada a la energía y el momento lineal, y la otra asociada al momento angular. Cuando pasa una onda, el tiempo entre que transcurre entre dos crestas se llama periodo, y su inverso es la frecuencia; la onda vibra en el tiempo con cierta frecuencia y según el teorema de Noether tiene una energía intrínseca, llamada energía, siempre que se pueda variar la fase de la vibración en el tiempo sin cambiar el perfil de la onda. La distancia entre dos crestas de una onda se llama longitud de onda, y su inverso es el número de onda. Una onda que se mueve en el espacio con cierto número de onda, según el teorema de Noether, tiene momento lineal si se puede variar la posición de esta vibración en el espacio sin alterar el perfil de la onda. Más aún, una onda puede vibrar en el espacio de tres dimensiones con simétrica rotacional y por ello tener un momento angular intrínseco respecto a un eje de giro, que se conservará si se puede rotar la onda respecto a dicho eje de giro sin cambar el perfil de la onda.
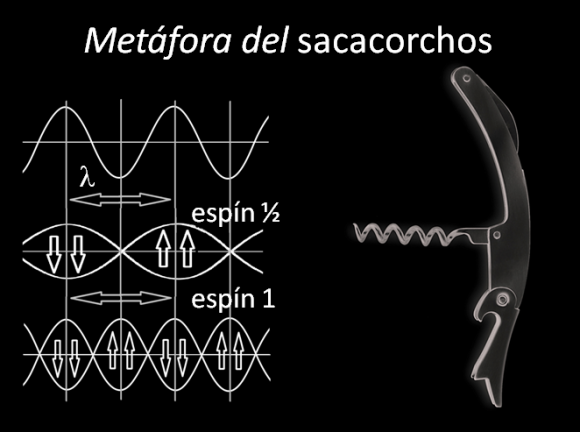
La partícula es una onda tridimensional con simetría esférica y por ello tiene momento angular intrínseco, llamado espín de la partícula. Podemos imaginar que la onda además de oscilar con crestas y valles realiza un movimiento en espiral, como un sacacorchos. El espín de la partícula nos dice de qué manera rota en espiral la onda asociada a la partícula. La frecuencia y la longitud de onda son valores continuos que pueden ser arbitrarios; sin embargo, el movimiento en espiral asociado al espín está cuantizado con respecto a la longitud de onda (o a la frecuencia). En la metáfora del sacacorchos, el espín nos dice cómo está cuantizado este movimiento espiral con respecto al movimiento de crestas y valles.
Un espín unidad significa que una vuelta de la espiral coincide con una longitud de onda, la distancia entre dos crestas (o dos valles); un espín dos significa que hay dos vueltas de la espiral en cada longitud de onda; en general, el espín entero cuenta el número de vueltas de la espiral que caben en una longitud de onda (entre dos crestas o dos valles seguidos). En la metáfora del sacacorchos, un espín semientero igual a un medio (1/2) significa que una vuelta de la espiral coincide con la distancia entre una cresta y un valle, la mitad de una longitud de onda; luego una espiral completa requiere dos longitudes de onda. Un espín igual a 3/2 significa que tres espirales coinciden con dos longitudes de onda; y así sucesivamente. En general, un espín semientero significa que un número impar de espirales cabe en dos longitudes de onda (la distancia entre tres crestas o tres valles); para espín entero habrá un número par de espirales entre dos longitudes de onda. Recuerda que los enteros son pares o impares, no hay otra posibilidad, lo que explica la cuantización del momento angular intrínseco o espín.
El espín de una partícula de un campo cuántico está cuantizado, como todo momento angular. Para una partícula con masa con espín , la proyección del espín sobre un eje de giro (que puede, o no, coincidir con la dirección de movimiento de la partícula) nos da
; en concreto, para espín 2 tenemos 5 valores del espín, para espín 3/2 tenemos 4 valores, para espín 1 tenemos 3 valores, para espín 1/2 tenemos 2 valores y para espín cero un solo valor (todo esto ya lo dijimos unos párrafos más arriba). En las partículas sin masa solo hay dos posibles valores del espín, sean
y
, sin que haya valores intermedios (pues la relatividad impide que nada viaje más rápido que la luz y obliga a las partículas sin masa a vibrar en un plano transversal a su dirección de movimiento).
Por cierto, en este contexto, la masa de una partícula es la energía mínima necesaria para excitar el vacío de un campo y producir un cuanto. Las partículas sin masa, como el fotón, son cuantos que se excitan a cualquier energía, tan pequeña como podamos imaginar. Las partículas con masa, como el electrón, son cuantos cuya excitación requiere añadir energía al vacío del campo (gracias a la desintegración de una partícula de otro campo que esté acoplado con el campo del electrón y que tenga una energía suficiente mayor que su masa.
La importancia del espín en Física de partículas es resultado de la diferencia entre partículas de espín entero y de espín semientero. Para entenderlo tenemos que recurrir al teorema CPT. La conjugación de carga C consiste en cambiar las partículas por antipartículas. La paridad P consiste en cambiar de signo las coordenadas espaciales y equivale a una reflexión en un espejo. La inversión temporal T consiste en cambiar el sentido de la flecha del tiempo, cambiar el futuro por el pasado. De estas tres operaciones la única que afecta al espín es la operación de inversión temporal T que cambia de signo los momentos angulares.
Toda teoría cuántica de campos que cumpla con las leyes de la relatividad (sea invariante Lorentz) y de la mecánica cuántica es invariante CPT, es decir, la física que describe no cambia si realizan en secuencia las operaciones C, P y T. Este teorema es difícil de demostrar con rigor, e implica que para toda teoría CP=T, C=PT y P=CT. Luego las violaciones de una de estas simetrías (como las que presenta la interacción electrodébil del modelo estándar) implica la violación de la otra pareja.
El teorema CPT afirma que un campo cuántico regido por las leyes de la relatividad y la mecánica cuántica es invariante ante la operación CPT, porque dicha operación equivale a rotar el sistema 180 grados. En un espacio euclídeo de dimensión par (2 o 4) cambiar de signo todas las coordenadas equivale a una rotación de 180 grados (si miras la figura verás que he realizado dos reflexiones especulares, una respecto al eje horizontal y otra respecto al eje vertical, resultando una rotación de la figura del pingüino). Pero el tiempo no es una coordenada como las demás; en un espaciotiempo de Minkowski de dimensión par (1+1, o 3+1) la operación PT no corresponde a una rotación de 180º, ya que las partículas se cambian por antipartículas. Hay que aplicar la operación C para obtener una rotación de 180 grados.
El teorema CPT nos dice, por tanto, que hacer experimentos de pie, o haciendo el pino, conduce al mismo resultado. Parece obvio en un espacio euclídeo, pero en un espacio minkowskiano implica conclusiones muy sutiles sobre cómo se relacionan las partículas con cierto espín (entero o semientero) con el propio espaciotiempo; en concreto, cómo ocupan el espaciotiempo.
¿Por qué hay que aplicar CPT en lugar de solo PT? Porque la inversión temporal T cambia el flujo de carga, sea negativa, del pasado al futuro por un flujo de carga, sea negativa, del futuro al pasado; pero la flecha de tiempo siempre va del pasado al futuro (si exigimos que la energía se positiva), luego hay que interpretar dicho flujo de carga como un flujo de carga positiva del pasado al futuro (como decía Feynman, lo que para un físico es una partícula yendo del futuro al pasado, para otro físico es una partícula yendo del pasado al futuro). Por tanto, para corregir el efecto de la operación T hay que cambiar partículas por antipartículas (aplicar la operación C).
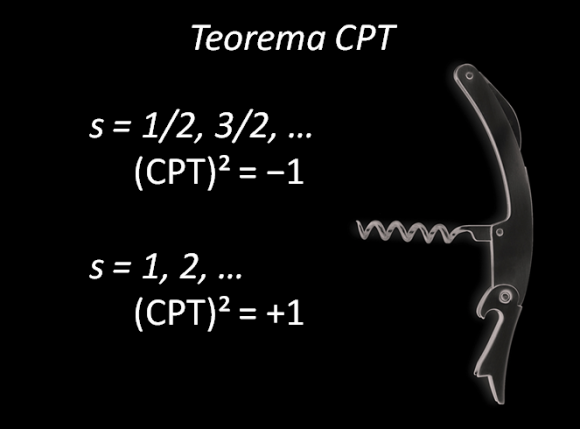
Aplicar dos veces la operación CPT equivale a rotar 360 grados, aplicarla cuatro veces a 720 grados. ¿Qué le pasa al espín al aplicar esta operación? Hemos visto que la inversión temporal T cambia de signo el espín. Las probabilidades no cambian, pero las amplitudes de probabilidad (o funciones de onda) pueden cambiar de fase. Resulta que para las partículas de espín entero, con (CPT)² = +1, una rotación de 360 grados las deja invariantes, pero para las de espín semientero, (CPT)² = −1, una rotación de 360 grados realiza un cambio de signo, no las deja invariantes; para ellas hay que rotar 720 grados (aplicar cuatro operaciones CPT) para dejarlas invariantes (sin cambio de signo).
Todo esto lo podemos entender gracias a la metáfora del sacacorchos. Para espín semientero, la espiral entre valle y cresta para un sacacorchos para diestros cambia tras la operación (CPT)² a una espiral entre cresta y valle de un sacacorchos para zurdos, luego aparece un desfase entre la onda de crestas y valles (asociada al momento lineal) y la onda asociada de espirales (asociada al momento angular). ¿Cuánto vale este desfase? Exactamente un cuarto de longitud de onda, o sea, 90 grados para la oscilación en amplitud.
¿Cómo este desfase de 90 grados explica el signo menos tras aplicar dos operaciones CPT? Como la función de onda cuántica está representada por una función con valores en los números complejos, un desfase de 90 grados equivale a la unidad imaginaria, la raíz cuadrada de menos uno (). Luego al aplicar dos transformaciones CPT (o sea, al rotar 180 grados) obtenemos que la amplitud de fase está multiplicada por
. Para espín entero esto no ocurre, siendo la clave que la componente de espín cero, con
; como ya sabes,
, luego solo puede haber un desfase de media longitud de onda, 180 grados (
). Ya que la operación CPT tiene que dar el mismo resultado para todas los componentes del espín, porque pueden estar en un estado de superposición cuántica, para espín entero (CPT)²=+1, y la amplitud de probabilidad no puede cambiar de signo al rotar 360 grados.
Mi experiencia con el público de Naukas indica que no es fácil entender este punto. La dificultad es que hay tener en cuenta dos movimientos simultáneos, el de la amplitud (asociado a la energía y el momento lineal) y el de la espiral (asociado al espín). Ambos están sincronizados, porque el momento angular está cuantizado, pero puede haber un desfase entre ellos. Este desfase en una operación CPT, rotar 180 grados, no puede ser arbitrario, porque solo estoy cambiando de signo la posición y el sentido del tiempo. En esta figura he dibujado el movimiento en espiral como una cinta torsionada; una cara es blanca con flechas negras y la otra es negra con flechas blancas, luego en la espiral se torsiona la cinta mostrando de forma alternativa caras blancas y negras (o flechas negras y blancas).
Quizás ayude recordar que hay sacacorchos diestros y zurdos, que han de ser rotados en sentidos diferentes para obtener el mismo resultado (o usando manos diferentes). Imagina el sacacorchos diestro funcionando (siendo rotado) en sincronía con la onda en amplitud; al aplicar la operación CPT es como cambiar el sacacorchos por uno zurdo que funciona al revés (rota en el sentido contrario). Para espín semientero, una espiral cubre dos longitudes de onda; imagina media espiral, que cubre solo una longitud de onda (dos crestas seguidas) moviéndose hacia la izquierda. Al aplicar CPT, reflejas esta media espiral en un espejo (cambias el sacacorchos de diestro a zurdo) y además pones la flecha del tiempo en dirección contraria (la media espiral se mueve hacia la derecha); como resultado dejan de estar sincronizados el movimiento en amplitud (que sigue siendo el mismo, pues el momento lineal o velocidad no ha cambiado) y el movimiento en espiral (lo que antes ocurría entre cresta y valle ahora ocurre entre valle y cresta). Así sale el desfase de 90 grados debido a la operación CPT.
¿Por qué es importante el cambio de signo tras una rotación de 360 grados para espín semientero? Para entender tenemos que recordar que las partículas son indistinguibles entre sí si tienen los mismos números cuánticos (la misma energía, momento lineal y espín, en el caso de una partícula libre); cuando tengo dos partículas A y B cercanas en las posiciones cercanas 1 y 2, no sé cuál es cuál y la función de onda que las describe es una superposición de |A1B2> + |A2B1>. Lo más curioso es que el intercambio de las partículas corresponde a una operación (CPT)², o sea, rotar 360 grados. La razón es que visto desde A, la partícula B rota 180 grados, y visto desde B, la partícula A también rota 180 grados.
Por tanto, para partículas de espín semientero, el intercambio conlleva un cambio de signo, |A1B2> = –|A2B1>, y la función de onda que describe las dos partículas es antisimétrica. Sin embargo, para partículas de espín entero, el intercambio no cambia el signo, |A1B2> = +|A2B1>, y la función de onda es simétrica. Este intercambio está en el origen del principio de exclusión de Pauli para los fermiones, que explica la estabilidad de los átomos y de la materia, y de la existencia de la estadística de Bose–Einstein para los bosones, que explica el láser, los superconductores y los condensados de Bose–Einstein.
Podemos entender la diferencia usando diagramas de Feynman (que él mismo usa en su charla de 1986). Un femión en cierta región del espaciotiempo es una excitación del campo sobre su estado de vacío, y por tanto está rodeado de fluctuaciones de vacío; de forma continua aparecen y desaparecen lazos en los que se crean una pareja partícula-antipartícula que se aniquilan de forma casi inmediata (siempre cumpliendo con el principio de indeterminación de Heisenberg, ). Si la partícula del lazo de vacío tuviera los mismos números cuánticos que la partícula, podría ocurrir un intercambio de sus identidades, como muestra el diagrama de Feynman.
Los cálculos indican que la amplitud de probabilidad de ambos diagramas sería idéntica; como para fermiones (CPT)² = −1, estos diagramas se restan (1−1=0) y la probabilidad resultante es exactamente cero. Por tanto, para un fermión es imposible (está prohibido) que el vacío fluctúe alrededor de una partícula con lazos cuyas partículas virtuales tengan los mismos números cuánticos; esto quiere decir que el femión ocupa espacio y no permite que nada fluctúe con sus mismos números cuánticos, ni siquiera el vacío. Aparece así el principio de exclusión de Pauli en todo su esplendor.
En un átomo los electrones se colocan en capas con diferentes números cuánticos; el campo del electrón para cada electrón puede fluctuar como ondas diferentes en la misma región, las maneras de oscilar del campo deben ser diferentes, porque si fueran iguales sus probabilidades se restarían y darían cero. El espín, vía el teorema CPT, explica por qué estamos aquí, por qué existimos, por qué hay estructuras materiales complicadas en el universo.
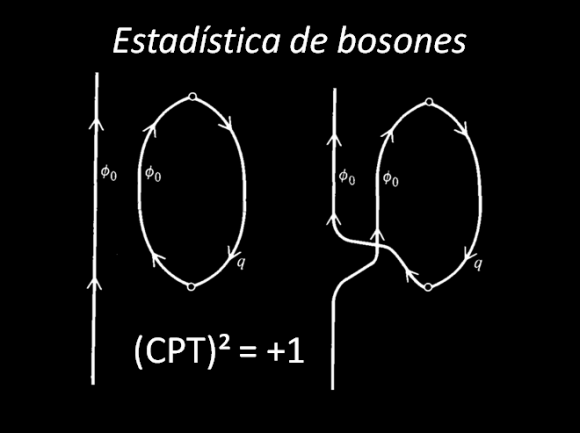
Para bosones ocurre todo lo contrario. El vacío alrededor de una partícula puede fluctuar con lazos cuyas partículas tengan los mismos números cuánticos. Recordando que para crear (excitar) una partícula hay que excitar con energía el vacío del campo, la existencia de lazos de vacío alrededor de una partícula con sus mismos números cuánticos implica que es más fácil excitar una partícula alrededor de una partícula ya existente que en el propio vacío; en concreto, la probabilidad de lograrlo se duplica. Si tenemos dos partículas hay tres diagramas de intercambio y la probabilidad de excitar una cuarta partícula se triplica. Por tanto, los bosones se comportan como si no ocuparan espaciotiempo y las vibraciones de muchos bosones con iguales números cuánticos se suman.
Un cálculo cuántico sencillo muestra que si tengo una partícula, la amplitud de probabilidad de producir una segunda partícula es veces mayor; si tengo dos partículas, es exactamente
veces mayor, y si tengo
partículas, la amplitud de probabilidad de crear la
-ésima es exactamente igual a
. Recuerda que las probabilides son los cuadrados de las amplitudes de probabilidad.
Este fenómeno explica la condensación de bosones que ocurre en los superconductores y en los condensados de Bose–Einstein. También explica la radiación estimulada, el secreto del láser que descubrió Einstein cuarenta años antes de que se fabricara el primero. Los bosones son partículas gregarias que prefieren estar todas en el mismo estado, mientras que los fermiones son partículas solitarias que no quieren ningún tipo de compañía.
Soy consciente de que mi explicación era demasiado abstracta para que Javier Peláez y el resto de la audiencia pudiera entenderla en una primera exposición. Sin embargo, como los vídeos de las charlas se pueden ver más de una vez, y como mi costumbre es escribir un artículo explicando su contenido, creo que he logrado un objetivo importante. Poner en valor el espín, como algo importante que el público debe conocer, y ofrecer un conjunto de palabras clave a quienes quieran profundizar, como la importancia del teorema CPT a la hora de entender las consecuencias del espín.
Por supuesto, me he dejado muchas cosas en el tintero, como la existencia de momentos magnéticos asociados al espín, que explican el magnetismo de la materia. También he obviado la teoría de las representaciones irreducibles de grupos de Lie y álgebras de Lie, que subyace a las propiedades cuánticas del momento angular, vía el grupo SO(3) o el álgebra so(3), y del espín, vía el grupo SU(2) o el álgebra su(2); introducir la teoría de representaciones irreducibles del grupo de Poincaré, el concepto de casimires, la relación íntima entre la masa y el espín para las partículas que se describen con funciones de onda en una representación, me habría llevado demasiado lejos, creo.
Como siempre, tanto si te gusta mi charla, como si no, te recomiendo disfrutar de las demás charlas. Aprenderás mucho y te divertirás muchísimo más.














Lo que entiendo entonces es que el spin, es ¿análogo a una onda (electromagnética) circularmente polarizada, pero para la función de onda? ¿Y de ahí se podría deducir alguna propiedad de quiralidad (giro dextrógiro / giro levógiro)?
Julio, cuidado, una onda polarizada circularmente tiene momento angular pero no tiene momento angular orbital, y por tanto no tiene pseudoespín. ¿No conoces el concepto de momento angular orbital?
Por otro lado, para explicar un concepto matemático sin usar matemáticas hay que usar una metáfora; como en electromagnetismo hay un concepto análogo al espín llamado pseudoespín, he decidido explicar en Naukas Bilbao el espín usando dicha analogía. Pero no es que el spín sea un «pseudoespín de una partícula» sino que el pseudoespín de una onda electromagnética tiene propiedades clásicas análogas a las propiedades cuánticas del espín de una partícula.
Cada persona será diferente, pero mi punto de vista es que la charla se entendía bien hasta que aparece el concepto de CPT. No pillar eso y luego los pingüinos me descolocaron y dejé de seguir. Creo que fue en ese momento que Irreductible soltó el «¡Jodeeeer!» y me sentí acompañado.
Luego te puede contar una anécdota BioTay, que en avión una señora mayor con acento extranjero le empezó a preguntar sobre el espín. La misma señora había con ido su hijo a todas las charlas y antes de subir a ese avión me preguntó a mí si había entendido «lo del espín». Sólo por ese detalle tu charla ya hubiera valido la pena, pero todo el debate que generó y los memes la hicieron indispensable.
Gracias, Txapulin, por tu comentario; varias personas me han comentado lo mismo: extender la primera parte (hasta CPT) a 10 minutos hubiera sido una charla redonda. El problema es que en dicho caso no hubiera podido decir que las partículas de espín semientero ocupan espacio y las de espín entero no lo ocupan, pues no se habría entendido sin hablar del cambio de signo en el intercambio.
La señora que comentas habló conmigo tras la charla. Me preguntó si «espín» y «spin» (en inglés) eran lo mismo; ya que como «spin» significa giro, me dijo, entonces para ella era más fácil imaginar que el espín de una partícula significaba que la partícula giraba y punto. Yo le comenté que mi explicación trataba de ir más allá, pues es difícil imaginar una partícula «puntual» girando y que lo que gira es algo «interno» a lo que hace que la partícula sea una partícula, la partícula como tal. Creo que no me entendió muy bien, o no supe explicarme bien, pero por lo que me dijo le gustó la charla.
Hola,
La pareja madre-hijo que coentais eramos mi madre y yo. Fue mi tercera visita a Naukas y la segunda de mi madre, además de haberla llevado a presentaciones de otros Naukers en Madrid. Y si bien es cierto que ni mi madre ni yo nos enteramos mucho, también es cierto que nos pasamos todo el fin de semana haciendo bromas sobre el espín. He vuelto a mirar el video y leído varias veces la entrada, y creo que ahora comprendo un poco más del espín, aunque no todo. LE dare otro par de lecturas y visionados.
Agradecer también mucho a Francis la explicación adiccionaal que dió a mi madre, la verdad es que le interesó mucho y le gustó cómo explicabas, se te nota la pasión en tus presentaciones.
Saludos,
Gracias, Nico, por tu comentario.
Francis, el escritor Haruki Murakami dice que escribir novelas NO es un trabajo para personas extremadamente inteligentes, porque son capaces de condensar en una frase todo lo que quieren decir, y la escritura es un trabajo que ha de ser de poco rendimiento…pues bien, para explicar cosas, también.
Cada frase de tu charla tiene un fondo gordo y nada trivial, basta con que uno necesite más de cuatro segundos con una de ellas, para perderse la siguiente y acabar fuera del hilo. De hecho pensaba que en mis 10 minutitos que me doy de descanso despachaba tu charla y no es así, la he cortado para atenderla con más tiempo.
Truco: Una vez tengas claro lo que quieres explicar, espera a la noche, cuando estés más cansado, para escribir la charla; así como la mejor literatura sale cuando uno está medio atontado, cuando la parte emotiva está sustituyendo a la parte racional adormilada, también para este tipo de cosas es positivo, pues eres más redundante y te cuesta expresarte, lo cual es ideal para el lego, ya que acabas repitiendo las cosas varias veces de distinta manera.
Truco2: Mándale la charla a un aficionado para que te diga si de una sola leída lo pilla. Yo mismo estaría encantado de leer cualquier cosa que vaya destinado a legos o aficionados cortos de mollera como un servidor, para echar una mano.
Gracias, Pedro, por el ofrecimiento; de hecho, tengo varios amigos cercanos a los que recurrir.
Querido Francis, el «espín», sinceramente, no llegué a entenderlo. Pero sí entendí una cosa, aunque no fue en el Palacio Euskalduna, fue fuera, en los bares, por la calle, hablando de tu a tu con uno de los tíos más geniales que he conocido. Un saludo, y espero que nos podamos volver a encontrar pronto en algún otro lugar. Agur
Una pena no haber acudido de forma presencial pero he visto la charla por internet y me ha gustado, igual era demasiada información para diez minutos, pero esta entrada ayuda a pensarlo con más calma.
A mi me encantó tu charla. Más aún, diría que fue soberbia. Vale, quizá no sea representativo de la audiencia, pero conseguí seguirte y vi cómo surgía una «justificación» del principio de Pauli. Lo tengo grabado a fuego: los bosones no ocupan lugar en el espacio-tiempo.
Gracias y saludos,
Juan Carlos—
@ApuntesCiencia
Al ver por enesima vez esta magistral charla no he podido evitar las siguientes explicaciones para dar satisfacción a la enigmatica cuestión del entrelazamiento cuantico.
Considero que cuando dos partículas entrelazadas y por tanto, conservación del entrelazamiento en sus respectivos espines se desplazan en dirección opuesta en el Espacio, implica que una esta viajando hacia el futuro tanto como la otra esta viajando al pasado respecto de la otra. La consecuencia es que al colapsar una de ellas en su momento presente es comprensible que la otra conserve el mismo momento presente respecto de la otra y de ahí que se conserve el comportamiento coherente esperado para el espin de una y de otra, es decir, la conservación instantanea de la información de ambas.
Quería volver aquí a comentar algo que ya comenté en Twitter y veo que Pedro Mascarós lo ha expresado estupendamente en sus dos primeros párrafos. Dice textualmente «Cada frase de tu charla tiene un fondo gordo y nada trivial» y estoy muy de acuerdo.
En mi opinión, ha sido la mejor charla de #Naukas17 con diferencia. Hay quien dice que le gusta la divulgación si aprende algo nuevo comprendiéndolo a la primera. Creo que esto es equivalente a que no les agrada salir de su zona de confort.
He tenido que verlo dos veces y ahora leer aquí tus apuntes de ampliación para consolidar conceptos.
GRACIAS FRANCIS.
Aprovecho aquí para preguntar algo relacionado, aunque no directamente, con la charla.
– Siempre se citan electrones como ejemplo del princ.excl. de Pauli. Pero ¿Se ha observado el principio de exclusión de Pauli con más de dos fermiones ocupando un mismo orbital? Por ejemplo, 4 partículas con spin 3/2.
¡Rayos y retruécanos!
Gracias de nuevo
¡Vámonos átomos!
Radiactivoman, como sabes, las únicas partículas fundamentales con espín 3/2 son los gravitinos, aún por observar, si existen. Hay partículas compuestas con espín semientero, todos los bariones lo tienen, habiéndose observado hasta espín 15/2; por desgracia aún no hemos observado moléculas hadrónicas de tipo hexaquark formadas por dos bariones con espín 3/2 (tampoco con cuatro).
Hay núcleos atómicos con espín semientero (O-17 y Na-23 tienen espín 3/2) pero no podemos entender de forma fácil un núcleo «compuesto» por ambos (como K-40) aludiendo a un movimiento orbital de estos núcleos «componentes».
Se requiere el uso del principio de Pauli para entender las moléculas formadas por átomos con espín 3/2 (en rigor momento angular total, orbital más espín). No recuerdo si hay alguna formada por cuatro átomos de espín 3/2, pero en su caso sería un ejemplo de lo que pides (aunque no sé si es lo que pensabas).
RadiactivoMan:
Muy buena pregunta. En principio las partículas (fundamentales) de espín 3/2 están prohibidas en la naturaleza. Un teorema de prohibición («no-go») explícito para este espín tiene por nombre Velo-Zwanziger.
(Técnicamente lo que está prohibido es el acoplamiento mínimo con el fotón y los demás campos de norma, que viene a ser equivalente a prohibir el campo de Rarita-Schwinger pues los acoplos reaparecen tras correcciones cuánticas y hay que suprimirlos a todo orden en teoría de perturbaciones)
Hay otros problemas más serios que prohiben la existencia de partículas de alto espín (por ejemplo 7/2, 4, 11 etc.) por mencionar dos ejemplos famosos son los teoremas de Weinberg-Witten y Colemann-Mandula (Qué técnicamente lo que hacen es restringir el tipo de cargas conservadas en vuestra teoría, lo cual es mucho más grave pues son restricciones explícitas para las simetrías de la matriz S, de hecho Coleman-Mandula explicíta la extensión máxima de una QFT con la simetría de Lorentz).
Sin embargo como bien dice Francis, Supergravedad (en todas sus variantes) precisa de un (o varios) super-compañero(s) para el gravitón. Lo maravilloso es que ninguno de los problemas mencionados (aplicados al campo de espín 3/2) son relevantes. Más aún, la única completación consistente de cualquier supergravedad es necesariamente alguna teoría de cuerdas (*Salvo una aclaración que hago abajo*) y cuerdas tiene en su espectro una torre infinita de partículas con masa y de espín arbitrariamente alto.
Aún más, es muy díficil construir teorías de alto espín, pero existen éxitos importantes como la teoría de Vasiliev, la construcción explícita de acoplos cúbicos, las álgebras de alto espín y un pequeño etcétera. Algunos de los progresos más relevantes de nuestros tiempos (motivo de breaktrought prize para jóvenes destacados) es que hay evidencia importante y altamente no trivial de que la torre de Vasiliev en ADS es un límite de teoría de campos de cuerdas con variedad objetivo ADSxCP^3, Klebanov y Polyakov conjeturaron que el sistema de Vasiliev era holográficamente dual a una teoría conforme con simetría O(N). Xi-Yin y Giombi demostraron que es cierto, hay una especie de trialidad Entre teoría de campos de cuerdas(O el modelo topológico tipo A)-El sistema de Vasiliev y una O(N)-CFT (En realidad calcularon las funciones de tres puntos en un arista de la trialidad y encontraron acuerdo, lo que es parecido a probar la conjetura perturbativamente pues usando la idea del bootstrap puedes factorizar la función de n-puntos en funciones de dos y tres puntos hasta funciones).
Moraleja 1: Teoría de cuerdas parece ser la única forma de acomodar una teoría de alto espín.
Moraleja 2: Aunque las teorías de alto espín son difíciles y muy restrictivas tienen duales holográficos muy simples y con un parámetro ajustable que viene de maravilla para hacer teoría de perturbaciones y un límite de N grande apropiado. Es una pregunta interesante saber si todas las teorías con duales holográficos se comportan así.
Lo anterior es superinteresante, yo llevo mas de cinco meses intentando entender la idea de la trialidad y no me resisto a comentar algo hermosísimo: Xi Yin interpreta una transición de fase en el Modelo O(N) como una fase de deconfinamiento en la teoría de cuerdas ¡Es una señal de confinamiento en teoría de cuerdas! ¡ 😀 ! y propone que las cuerdas se deconfinan en preones de alto espín y conjetura que son partículas del sistema de Vasiliev. Cuerdas tiene una historia de mares de similaridades con QCD, los modelos duales, el límite de N grande, QCD en 2d=Teoría de cuerdas, modelos matriciales y ahora… ha sonado la campana de confinamiento 🙂
Buffff, qué complicado…
Estimado Pedro:
Le ofrezco una disculpa. Este es un claro ejemplo de como a alguien que le apasionan estas cosas (Yo) es un pelmazo e incapaz de explicar con la simplicidad que lo hace Francis. Que fortuna es que le tengamos para explicarnos estas cosas a los demás.
Pedro:
A manera de disculpa sólo quería decir que la pregunta de la existencia de campos de alto espín (fundamentales) en la naturaleza es importante. Tiene mucho que ver con el concepto mismo de espaciotiempo.
Hablando mal se puede decir que la razón por la cual no observamos partículas de espín 3/2 (fundamentales) es porque vivimos en el vacío del campo de espín dos y para observar un gravitino debemos explorar otra faceta del espaciotiempo (el superespacio), cosa que no es fácil.
Para observar campos de alto espín de nuevo necesitamos observar otra metamorfosis del espaciotiempo y vivir en el vacío de algún otro campo de alto espín. Como dato curioso: Nadie entiende aún la geometría de las ecuaciones de estos campos ni como modifican al espaciotiempo. Pero es trabajo importante y está en progreso 🙂
Un saludo Pedro
Muy interesante Ramiro. ¿podrías aclarar un poco más a que te refieres con el «superespacio» en el comentario anterior?
Personalmente estoy bastante interesado en las teorías de alto spin (HST) sobre todo en la teoría de Vasiliev aunque la complejidad Matemática me supera en varios aspectos de la teoría. Por lo poco que se las HST podrían dar soluciones a (como mínimo) cinco cuestiones fundamentales de la Física actual:
1º) Al ser una teoría de máxima simetría se relaciona con procesos que suceden a escalas inferiores a la escala de planck donde vive la gravedad cuántica. Además, como dices, parece que String Theory podría ser un límite de las HST. ¡Las HST podrían esconder el secreto de la gravedad cuántica!
2º) Podrían ayudarnos a desarrollar por fin una dualidad dS/CFT y poder aplicar principios holográficos a nuestro Universo dS
3º) Nos permitirían describir nuevas geometrías o» geometrías ocultas» de nuestro Universo. No comprendo muy bien el concepto de «space-time metamorphoses» en HST pero parece que la geometría no depende del «world volumen» sino que está codificada en funciones del «target space» y la dinámica descrita por las HST (teoría de Vasiliev) permitiría nuevas geometrías con conexiones que describen nuevos vacíos no triviales.
4º) Nos pueden dar pistas sobre el origen de los principios de la mecánica cuántica: ¡La teoría relativista HST es holográficamente dual a la teoría cuántica no relativista! ¿Qué puede significar esto? Y por cierto ¿que puede significar que en clasical HST exista una diferencia explícita entre un espectro de frecuencias positivas y otro de frecuencias negativas? ¿Que diablos es una frecuencia negativa?
5º) Las HST nos podrían ayudar a encontrar una solución al problema de la paradoja de la información de los agujeros negros.
Casi nada… ¿Serán las HST la solución a gran parte de los enigmas pendientes de la Física moderna?
Con mucho gusto me explico Planck. Con «superespacio» me refiero a que hay formulaciones geométricas de supersimetría en donde se añaden variables fermiónicas al espaciotiempo además de las bosónicas usuales (Cuando sea posible). Por eso decía que descubrir una partícula supersimétrica (particularmente el gravitino) a baja energía (digamos LHC) es «la misma cosa» que descubrir una dimensión extra fermiónica atípicamente grande.
Ya somos dos los interesados en teorías de alto espín 🙂 (y también somos dos a quienes nos supera su Física y Matemática).
3.- Lo de las «spacetime metamorphoses» es una expresión a un cúmulo de (interesantísimas) especulaciones de Vasiliev. Una de ellas se refiere a que si dos espaciostiempos tienen el mismo espacio twistor entonces son holográficamente duales. El ejemplo típico es el famoso ADS(5) cuyo espacio twistor es (formalmente) idéntico al espacio (Ambi)Twistor de su frontera.
También se refiere al hecho que mencionaba de que el espaciotiempo a baja energía es un vacío para el campo del graviton; pero los campos de alto espín también deberían un estado de vacío que corrija esta imagen, lo emocionante es que Vasiliev mismo reconoce que no hay un formalismo geométrico para hacer esto, nadie sabe qué matemática hay detrás y de hecho la primer conjetura que menciono sólo tiene tres ejemplos (El clásico de Ads5xS^5 y teoría M en Ads4xS7 y Ads7xS^4).
De hecho no saber cual es la geometría que realiza como simetría el álgebra de alto espín es un problema práctico, para evitar calcular en string field theory podría intentarse calcular en un modelo A topológico para hacer simples las cosas (Además una de las aristas de la trialidad es Cuerdas IIA en Ads4xCP^3) sin embargo como no sabemos la geometría de fondo no sabemos tampoco cuales son sus deformaciones consistentes y entonces la cuerda topológica calcula nada en este contexto.
¿Cómo modifica la existencia de partículas de alto espín nuestra idea de espaciotiempo?, ¿Cómo afecta la dinámica cosmológica y ultravioleta de la teoría de Einstein? las preguntas siempre son fáciles 🙂
5.- ¿Algo tienen que decir sobre la paradoja de la información?. Seguramente si 🙂 hay papers donde se argumenta que los teoremas de no pelo operan en el espaciotiempo de la relatividad general, si consideramos el vacío de alto espín es posible que los agujeros negros admitan cargas conservadas de alto espín.
Muchos saludos planck!
Gracias Ramiro por tus aclaraciones. Desde luego es increíble el poder de las Matemáticas y la Física, el solo hecho de poder acercarnos a cuestiones tan profundas es impresionante. Es cierto que nunca las Matemáticas fueron tan abstractas y difíciles pero también es cierto que nunca el premio a conseguir fue más elevado y trascendente. Un saludo Ramiro.
La charla es muy buena como de costumbre y la explicación de la diferencia entre bosones y fermiones es brillante. Además Francis ha conseguido que durante un rato un montón de gente hable de Física fundamental lo cual es algo muy difícil de conseguir. Me gustaría hacer un par de comentarios al respecto:
– En primer lugar, como Francis ya ha dicho en muchas ocasiones, los fenómenos cuánticos no tienen analogías clásicas exactas por lo que cualquier sistema Físico clásico cotidiano que utilicemos siempre será incompleto. Nuestro cerebro, para entender como funciona algo necesita recurrir a visualizaciones de algo que sea intuitivo o cotidiano y los fenómenos cuánticos (y relativistas) como el spin no se pueden describir ni comprender completamente en estos términos.
– En segundo lugar, la única forma que existe para describir de forma completa un fenómeno como el spin de una partícula fundamental es a través de las MATEMÁTICAS. A través de las Matemáticas y de ciertas leyes Físicas conocidas llegamos a una serie de relaciones y de características que una partícula fundamental como el electrón debe de cumplir. Por ejemplo, para cumplir con los principios básicos de la relatividad de forma que todos los observadores midan los mismos invariantes relativistas, la partícula (la vibración del campo cuántico) debe ser invariante bajo el grupo de Poincaré, este grupo incluye las transformaciones de Lorentz (boost) y las rotaciones. Estas rotaciones están constituidas por el spin y momento angular orbital. Es decir, para cumplir con los principios relativistas la partícula debe de realizar algo parecido a un giro pero este giro no tiene nada que ver con un giro cotidiano como el de la esfera en un espacio 3D, es otra cosa, es algo que no tiene nada que ver con nada que hayamos visto en nuestro mundo macroscópico. Para describir este giro debemos recurrir a espacios Matemáticos abstractos donde residen los spinors, la funcion de onda compleja, las componentes quirales que se expaden, se comprimen y se reflejan, las proyecciones sobre el vector de estados en el espacio de Hilbert cuando medimos etc, etc.
La pregunta clave inevitable es: ¿donde «residen» estos espacios y entidades Matemáticas? ¿cual es su «grado» de realidad? ¿debemos considerar todas estas entidades Matemáticas como reales o solo son reales las magnitudes Físicas medibles experimentalmente? Y por último (esto ya es especulación mia): ¿Son todas estas entidades y espacios Matemáticos una consecuencia de una estructura interna «no convencional» del propio espacio-tiempo? Estas preguntas forman parte del fascinante debate entre Matemáticas y realidad. Una cosa parece clara: La Física, las Matemáticas y la realidad están inextricablemente unidas.
Buen comentario Planck!
Yo también creo que el punto de la cuestión está en las matemáticas 🙂
Comparto una charla del grandísimo Atiyah sobre el concepto de espinor
https://www.youtube.com/watch?v=SBdW978Ii_E
Muchas gracias Ramiro por el enlace y por tus siempre interesantes comentarios. Un saludo.
Había leído que la gran dificultad para entender el espín de una partícula como momento angular es que ésta no es una bolita que rota, sino que es “puntual”… Si “punto” es un objeto matemático adimensional, sin longitud, área, volumen, etc. y si en realidad una partícula es una “excitación de un campo cuántico”…. ¿a qué os referís los físicos cuando decís que una partícula es “puntual”? ¿O estamos ante otra desafortunada analogía?
Gabriel:
Particula puntual es otra desafortunada analogía 🙁
(casi) Todas las excitaciones de un campo tienen una logitud de onda característica. Un fotón por ejemplo tendrá alguna frecuencia y por consiguiente una longitud de onda.
Pero como los «objetos cuánticos» como un positrón o un átomo de oro tienen una escala característica de energía muy pequeña comparada con los objetos que usamos para probarlos (detectores) a fines prácticos los podemos considerar como puntuales ¿Por qué? simplemente porque hacer cálculos es más fácil si suponemos que son puntos en lugar de distribuciones en el espacio.
Aunque existen objetos que en principio si son puntuales, como los intantones pequeños (que de cualquier forma existen formas de entender que son singularidades de los campos y puden resolverse definiendo el campo de otra forma cerca del instanton pequeño)
Gabriel, como bien dice Ramiro, «puntual» significa que tiene un tamaño pero que este tamaño depende de la energía, en concreto, el tamaño decrece conforme crece la energía-momento usada para medir dicho tamaño. Nada más y nada menos. Si para explorar dónde está un electrón en un átomo usas fotones con una energía de MeV lo localizarás en una región mil veces más pequeña que si usas fotones de keV y mil veces más grande que si usas fotones de GeV. El límite actual medido de forma directa, obviamente, se ha obtenido con el LHC: para energías de pocos TeV es menor de 10^-20 m (decenas de zeptómetros). Con estimaciones indirectas se estima que con seguridad no está compuesto a distancias superiores a 10^-22 m (décimas de zeptómetro); por debajo de esta escala no sabemos si está compuesto o sigue siendo elemental, pero en este último caso se espera que su tamaño decrezca hasta decenas de escalas de Planck conforme la energía del fotón que uses para explorarlo se acerque a la energía de Planck.
Espinores: no se adoptan porque los físicos sean pedantes o quieran usar palabras y conceptos «fancy». Hay dos razones básicas:
1) Como bien explica Francis. Sin Matemáticas simplemente no se puede «entender» (que para un físico entender =hacer predicciones correctas de experimentos). La aportación de Francis es traernos analogías que nos engañen mucho a los legos y que puedan capturar aspectos importantes.
2)El peligro que mencionas no existe. Justo porque los espinores elevan la discusión a un nivel semántico que anula la posibilidad de ambiguedad.
Si lees es el libro «Spinors and Spacetime» de Rindler y Penrose, os dareís cuenta de que el concepto de «dirección» no es geométricamente importante (invariante por transformaciones de lorentz) como tampoco lo son las coordenadas y los espinores son objetos cuya definición no depende de que puedas darle cartas al espaciotiempo.
El rol de los espinores en la física cuántica relativista es hacer absolutamente precisa la noción de espín.
Para ayudar a entender la entrada de Francis creo importante que se preste atención a estos artículos donde explica cuestiones igual de difíciles que el concepto de espín como lo son el concepto de electrón y de campo en teoría cuántica de campos.
Qué es un electrón en teoría cuántica de campos
https://francis.naukas.com/2013/01/09/que-es-un-electron-en-teoria-cuantica-de-campos/
Francis en @TrendingCiencia: La realidad está hecha de campos, no de partículas
https://francis.naukas.com/2013/12/02/francis-en-trendingciencia-la-realidad-esta-hecha-de-campos-de-particulas/
Una disculpa por comentar dos veces:
En este otro post Francis explica las sutilezas del concepto de partícula y como este deja de tener sentido en espaciotiempo curvo
Las partículas que emiten los agujeros negros por radiación de Hawking
https://francis.naukas.com/2013/02/05/las-particulas-que-emiten-los-agujeros-negros-por-radiacion-de-hawking/
Debeís leerle, es divertidísimo y sorprendente. Estas son de las cosas que ofrece Francis, que casi ningún otro divulgador hace (aún gente admirable como Brian Greene).
Como te dije muy brevemente en un descanso de pasada, yo sí lo entendí.
Gran charla.
El problema es que desde lo de CPT casi todo el mundo se perdió y tiró la toalla de seguir intentando entender. Pecaste de avaricioso xD
Yo me habría limitado al spin incluso usando otro punto de vista distinto con otra analogía para intentar explicar el spin por otro lado.
Felicidades, es una lástima que mi timidez me impidiera cruzar más palabras contigo.
BloodStar, tienes toda la razón, pequé de avaricioso. Me lo han comentado varios, debería haber prescindido de la parte de CPT y haber extendido la primera parte a toda la charla. Pero como de los errores se aprende, espero no tropezar de nuevo en la misma piedra.
Madre mía, te habrás quedado agusto, la verdad es que es un tema muy interesante, no me lo he acabado de leer entero todavía, volveré más tarde a verter mi impresión final, y sí, creo que es un tema infrexplicado en el mundillo, (como algunos otros tambíen, ojo)
Soy un doctorado en medicina, que se matriculó en primero de Física tras la licenciatura, y que, desgraciadamente, abandonó a los pocos meses. No menosprecio una exposición reglada, pero si me hubieran dado una charla como ésta, en vez de un teorema tras otro y una deducción, ecuación a ecuación, puede que mi limitada mente biologicista no se habría rendido tan pronto.
Gracias mil.
Por primera vez veo como asumible la dualidad onda-particula, el modelo estándar y dónde chocan la Relatividad y la Mecánica Cuántica.
Un abrazo
Por cierto, la quiralidad tiene un papel tan singular y fascinante en la biología molecular, el desarrollo embrionario y hasta en la neurología, que estoy por exclamar:
«Dios mío, está lleno de sacacorchos…»
Gracias por la referencia a los libros. Tu resumen es otro Gold Nugget más.
Solamente, hay un pequeño typo creo (en tu charla sí lo dices bien), propongo lo siguiente, como veas:
“En la metáfora del sacacorchos, un espín semientero igual a un medio (1/2) significa que media vuelta de la espiral coincide con una longitud de onda, es decir, la distancia entre dos crestas (o dos valles); luego una espiral completa coincide con dos longitudes de onda, es decir, la distancia entre tres crestas (o tres valles).
dice Paul Davies que el electròn da un giro de spin y desaparece del universo, pero que para volver al universo debe dar 2!!
Francisco, muchísimas gracias por tú aportación. Me ha encantado. Yo la verdad es que soy de económicas. Simplemente quiero comprender hasta que punto entendemos el origen del Universo y busco explicaciones como la tuya, que me hacen mucho más sencillo comprenderlo. Si me permites un minuto me gustaría hacerte unas preguntas que me han surgido tras leer el blog, para que me des tu opinión, aun si algunas cosas no están claras aún (por favor entiene que no tengo conocimientos del tema, sólo muchísimo interés en lo que voy leyendo): si nos remontamos al origen del Universo. Supongamos que no existía el espaciotiempo, ¿podrían existir los quarks sin espaciotiempo? Sobre el origen del espaciotiempo: En caso afirmativo, ¿crees que podrían los quarks «generar» espaciotiempo por sus propiedades interactuando entre ellos o tiene que existir el espaciotiempo para que interactuen? ¿Qué tiene que darse para que lo «generen» en ese caso, energía? Sobre el origen de la energía: La interactuación entre ellos mismos, por las propiedades que comentabas, ¿podrían haber generado energía o tiene que provenir de una fuente externa a ellos por mínima que sea? ¿Qué sería de los quarks sin energía? ¿y sin energía ni esapciotiempo? Sobre el efecto de los quarks en su «entorno»: ¿los quarks están condicionados por su «entorno» o es el «entorno» el que condiciona los quarks? Estoy intentando entender un artículo que leí que esta relacionado con tu exposición: He leído que el que la materia curve el espacio tiempo por la gravedad podría ser porque «absorbe» una porción de espacio abosrbiendo energía oscura balanceando así la cantidad de energía positiva y negativa totales.¿podrían los quarks actuar de la misma manera absorbiendo energía positiva y negativa y por ello ser su comportamiento una función de onda con diferente signo según cuando la observes y estar condicionados por la energía que «absorben» o liberan en cada momento y ser impredecibles por la aleatoriedad del «entorno» por el que «circulan»? Sé que hay varias preguntas que podrían ser contestadas por el blog pero sería un placer entenderlas en esencia y sé que otras preguntas serán tonterías. Perdonad todo el foro por mi falta de cultura en esto! opr algo me metí a económicas 😉 Mil gracias de verdad. Seguiré tu blog
Disculpa lo extemporáneo de mi comentario. He visto y leído en dos momentos distintos esta charla-entrada de blog y siempre me rechina la denominación de «espiral» para la forma tipo sacacorchos. A eso me enseñaron a llamarlo hélice (gira a distancia constante del eje de avance). Llamo espiral a la curva que se va alejando progresivamente del centro o eje de giro. De sobra sabes que las definiciones paramétricas de ambas curvas son completamente diferentes. ¿Sigo actualizado o me he perdido algo? PD. Excelente acto de divulgación valiosa. Gracias.
Luis, tienes razón, debería haber usado hélice en lugar de espiral.