La predicción teórica más precisa de toda la física de partículas es el momento magnético del electrón. Por desgracia, la predicción para el momento magnético del muón difiere a 3,6 sigmas del valor observado. Tres físicos japoneses proponen una solución sorprendente: la contribución de la curvatura del espaciotiempo en la ecuación de Dirac para el muón. La gravedad en la superficie de la Tierra causaría la anomalía según un cálculo postnewtoniano publicado en tres artículos. Se soñaba con que la anomalía fuera la primera señal de nueva física más allá del modelo estándar. Por fortuna, a finales de 2018 el experimento Muon g–2 en el Fermilab publicará resultados que confirmarán o refutarán la nueva predicción teórica.
[PS 04 Feb 2018] Como ya dije en Twitter (10:44, 02 Feb) «El cálculo es tan sencillo y cuadra tan bien que suena a numerología. No sé, pero me huele mal. A pesar de ello, no encuentro ningún error en los papers» (aunque olvidé comentar mi lectura diagonal de los mismos). Como comenta Dam T. Son el cálculo viola el principio de equivalencia, luego es incorrecto. Y como comenta Diego M. el cálculo depende del potencial gravitatorio terrestre, luego es incorrecto pues en la superficie terrestre el potencial gravitatorio solar es 14 veces mayor, y además usa un sistema de coordenadas fijo, luego no es independiente del gauge y, por tanto, el resultado no es medible mediante experimentos. Pido perdón a los lectores por haberme dejado llevar por una lectura rápida de los artículos… la numerología es tan bonita y tan pseudocientífica.
De hecho, el cálculo japonés usa una aproximación postnewtoniana a la relatividad general, pero se usa para calcular un efecto que incumple con la hipótesis postnewtoniana (ϕ/c<<1); un cálculo postminskowskiano hubiera sido más riguroso, pero entonces el efecto desaparece. Seguro que la semana próxima aparece en arXiv algún artículo desmontando en detalle la numerología japonesa. [/PS]
El momento magnético del electrón y del muón es g μB, donde μB es el momento magnético de Bohr y g es un coeficiente que según la ecuación de Dirac debe ser g = –2. Los efectos cuánticos del vacío de la electrodinámica cuántica (QED) modifican este valor. Para el electrón se observa ge ≈ –2,002 319 304 361 82(52), que coincide con 13 dígitos decimales con la predicción teórica (cálculo QED a cinco lazos o loops). Sin embargo, para el muón se observa gμ ≈ −2,002 331 841 8(13), que difiere a 3,6 sigmas de la predicción teórica. La anomalía se suele cuantificar con el parámetro aμ = gμ/2−1. El nuevo trabajo afirma que bajo un potencial gravitacional ϕ se modifica su cálculo de de tal forma que aμϕ = aμ+ϕ/c2(4+aμ+3/(γ2−1)), con γ el factor de Lorentz. Para el muón en el anillo de almacenamiento se usa γ = 29,3 para suprimir la contribución del campo eléctrico lo que ofrece aμϕ = aμ + 2,8 × 10−9, que coincide con la anomalía observada aμ(EXP) − aμ(SM) = 28,8 (8,0) × 10−10. Al tomar como nueva predicción teórica gravitacional aμϕ(EXP) − aμ(SM) = 0,8 (8,0) × 10−10, en perfecto acuerdo con el modelo estándar.
¿Por qué el efecto gravitacional afecta a al muón pero no al electrón? Porque el momento magnético anómalo se mide de forma diferente en ambos casos. Para el electrón se usa una trampa de Penning en la que que se estima ae = (Ωs−Ωc)/Ωc, donde la corrección gravitacional se cancela al afectar por igual a la frecuencia de precesión Ωs y a la frecuencia ciclotrón Ωc. Para el muón se usa un anillo de almacenamiento y esta cancelación no se produce.
Los artículos son Takahiro Morishima, Toshifumi Futamase, «Post-Newtonian effects of Dirac particle in curved spacetime – I : magnetic moment in curved spacetime,» arXiv:1801.10244 [hep-ph], Takahiro Morishima, Toshifumi Futamase, Hirohiko M. Shimizu, «Post-Newtonian effects of Dirac particle in curved spacetime – II : the electron g-2 in the Earth’s gravity,» arXiv:1801.10245 [hep-ph], y Takahiro Morishima, Toshifumi Futamase, Hirohiko M. Shimizu, «Post-Newtonian effects of Dirac particle in curved spacetime – III : the muon g-2 in the Earth’s gravity,» arXiv:1801.10246 [hep-ph]. Más sobre el estado experimental de la anomalía recomiendo The Muon g−2 collaboration, «The Muon g−2 Experiment Overview and Status,» arXiv:1712.05980 [hep-ex].
Más información divulgativa en Tommaso Dorigo, «Gravitational Effects Explain Muon Magnetic Moment Anomaly Away!!» AQDS, 01 Feb 2018; Luboš Motl, «Earth’s gravity correction removes muon’s g−2g−2 anomaly: papers,» TRF, 01 Feb 2018; Peter Woit, «Muon g-2 Anomaly Gone?» NEW, 01 Feb 2018.
[PS 04 Feb 2018] Tommaso Dorigo, quien lanzó la liebre, comentó en Twitter que un cálculo teórico independiente (que se publicará la semana que viene) determinó que los efectos gravitacionales en g–2 son despreciables y que los japones habían omitido por error un término en sus cálculos.
[PS 05 Feb 2018] El portavoz del experimento Muon g-2, Chris Polly, afirma que los japones han estimado mal la magnitud del campo eléctrico en su experimento; el campo E es unas 1330 ppm el campo B, en lugar de ser comparable, luego la contribución gravitacional debida al campo E es como mucho de 2 ppb, despreciable ante un efecto observado de ~100 ppb. Polly hace notar que tanto si el cálculo de los japoneses es correcto, como si no lo es, su efecto es dos órdenes de magnitud más pequeño de la anomalía [/PS]. [PS 06 Feb 2018] El cálculo se publica en Pawel Guzowski, «The effect of Earth’s gravitational field on the muon magic momentum,» arXiv:1802.01120 [hep-ph]. [/PS]
Muchos comentarios en los blogs de Dorigo, Motl y Woit muestran que el cálculo japonés es pura numerología. Recomiendo leer a Luboš Motl, «Experiments may only measure gauge-invariant, coordinate-independent quantities,» TRF, 04 Feb 2018. Siento, de verdad, todas las molestias causadas por mi entrada. En parte me dejé llevar por el argumento de autoridad, ya que los trabajos previos de Hirohiko M. Shimizu me parecen muy interesantes y me olvidé de que su firma quizás sea accidental (son los tres primeros artículos del primer autor, Takahiro Morishima, y, casi, del segundo autor, Toshifumi Futamase); quizás Shimizu ha firmado los artículos tras una lectura diagonal como la mía. [/PS]
[PS 05 Feb 2018] Una crítica sencilla (los japoneses violan el principio de equivalencia) de Matt Visser, «Post-Newtonian particle physics in curved spacetime,» arXiv:1802.00651 [hep-ph]. Otra crítica, más rotunda, en Mark Goodsell, «Update on muon g-2: story of a debacle,» Real Self-Energy, 03 Feb 2018. [/PS]
[PS 05 Mar 2018] H. Nikolic, «Can effective muon g-2 depend on the gravitational potential?» arXiv:1802.04025 [hep-ph]; Andras Laszlo, Zoltan Zimboras, «On the quantification of GR effects in muon g-2 experiments,» arXiv:1803.01395 [gr-qc][/PS]
Esta fotografía muestra el experimento Muon g−2 instalado en el Fermilab cuyo objetivo es mejorar en un factor de 4 la precisión actual para aμ(EXP), lo que podría llevar a que la anomalía respecto a aμ(SM) pase de 3,6 sigmas a unas 7,0 sigmas. Por cierto, como curiosidad, su traslado por barco y helicóptero desde el BNL en Upton (cerca de New York) hasta el Fermilab en Batavia (cerca de Chicago) fue noticia en este blog («El momento anómalo del muón y el traslado del experimento E821 del BNL al Fermilab», LCMF, 21 May 2011).
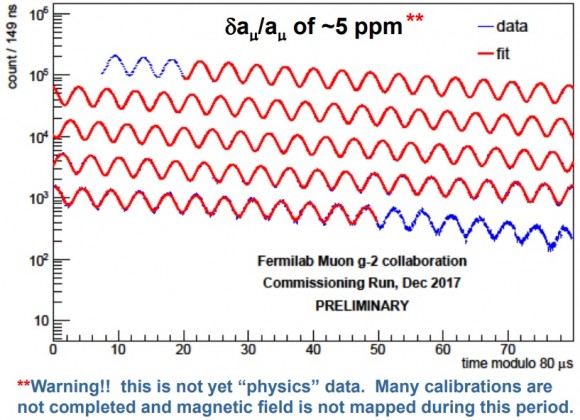
La toma de datos todavía no se ha iniciado. Este figura muestra un resultado preliminar a 5 ppm obtenido en la fase de calibración del experimento. El objetivo del experimento es reducir las 540 ppb de BNL a unas 140 ppb. La toma de datos está a punto de empezar y se espera un primer resultado científico a finales de 2018 o principios de 2019.

El nuevo resultado gravitacional japonés llega en el momento más oportuno y será confrontado con los primeros resultados de este experimento (a finales de este año o principios del próximo). Mucha gente es pesimista sobre el estado actual de la física de partículas. Pero el gran número de resultados experimentales que se están obteniendo y están próximos a ser obtenidos indican que, sin lugar a dudas, estamos viviendo épocas más apasionantes en la física de partículas en el siglo XXI.



Parece que el resultado viola el principio de equivalencia de Einstein: en un ascensor en caída libre no hay ningún efecto gravitacional. Se puede objetar que el laboratorio no está en caída libre, pero entonces la magnitud del efecto debe depender solo de la aceleración (9.8 m/c^2), pero no del potencial gravitacional.
¿El resultado depende del potencial gravitatorio? ¿Y no está fijado el gauge?
Hola Francis,
Queria saber tu opinion de otro articulo que ha salido recientemente sobre una explicacion de la medida del decaimiento del neutron basada en la materia oscura.
Muchas gracias
Javier, supongo que te refieres a «Vida media del neutrón y materia oscura», NeoFronteras, 21 Ene 2018, sobre Bartosz Fornal, Benjamin Grinstein, «Dark Matter Interpretation of the Neutron Decay Anomaly,» arXiv:1801.01124 [hep-ph].
Había dos métodos para medir la vida media del neutrón libre (que se desintegra en un protón). Usando neutrones ultrafríos se estima 879,6 ± 0,6 s y usando haces de neutrones se estima 888,0 ± 2,0 s; ambos métodos difieren a 4,0 σ. Un nuevo tercer método estima 878,1 ± 2,8 (C. L. Morris et al., «A new method for measuring the neutron lifetime using an in situ neutron detector editors-pick,» Review of Scientific Instruments 88: 053508 (2017), doi: 10.1063/1.4983578). Parece que el valor anómalo es el de haces de neutrones. ¿Por qué? La explicación más razonable es que hay errores sistemáticos en el método de medida basado en haces (de hecho, el más complicado de analizar).
El nuevo artículo afirma que el valor con el método de haces no tiene errores y lo usa como prueba de la existencia de una partícula de materia oscura (n -> p + x); no hay pruebas de dicha partícula ni de sus modos de desintegración, luego debería desintegrarse de una manera no explorada en este método, por ejemplo, en fotones, en cuyo caso tendría una masa entre 0,782 MeV y 1,664 MeV.
¿Qué me parece la idea? No está mal, pero debería haber muchas señales de dicha partícula oscura en procesos astrofísicos y terrestres, y no las hay. Luego pinta mal. Aún así, lo bueno es que la idea es fácil de contrastar con experimentos. En pocos meses debería haber artículos que refuten la idea. Si no los hay, habrá que buscar los supuestos fotones en los experimentos con haces de neutrones. La esperanza es lo último que se pierde.
Saludos
Francis