La turbulencia es uno de los grandes retos del siglo XXI. En una tubería rugosa el flujo turbulento se caracteriza por el llamado factor de fricción de Darcy, que depende del número de Reynolds. En 1962 Robert Kraichnan predijo un régimen turbulento cuyo factor de fricción no depende del número de Reynolds en el problema de Rayleigh–Bénard, un fluido en un recipiente calentado por debajo. Se publica en Nature Physics la primera observación experimental de este fenómeno, aunque se usa el problema de Taylor–Couette, un fluido entre dos cilindros concéntricos que rotan a diferente velocidad. Para lograr que la turbulencia no dependa de la fricción se introducen pilares empotrados (riblets) en el interior de ambos cilindros; esto simula una rugosidad de pared con una escala mayor que los vórtices más pequeños.
El número adimensional de Reynolds (Re) es el cociente entre las fuerzas inerciales y las fuerzas viscosas en el fluido. En una tubería rugosa, a partir de cierto número de Reynolds crítico (~3500) aparece la turbulencia; en dicho régimen la resistencia al flujo sigue la ecuación de Darcy–Weisbach, siendo proporcional al cuadrado de la velocidad media del fluido. Esta fricción depende del valor de Re vía la ecuación de Colebrook (1939) para el factor de fricción de Darcy, Cf.
El problema de Rayleigh–Bénard se caracteriza por los números de Nusselt (Nu), cociente entre la transferencia de calor por convección y por conducción, y de Rayleigh (Ra), la versión adimensional de la diferencia de temperatura entre el fluido en el fondo y en la parte superior. Según la teoría de Kraichnan, para alto Ra, aparece un régimen turbulento descrito por una ley de escala Nu = Ra1/2, con Cf independiente del número de Reynolds.
El problema de Taylor–Couette se caracteriza por el número de Nusselt equivalente (Nuω) y por el número de Taylor (Ta), análogo al número de Reynolds para las fuerzas centrífugas. La teoría de Kraichnan predice que, para alto Ta, se tiene Nuω = Ta1/2, con Cf independiente de Re. Esta predicción ha sido confirmada tanto numérica como experimentalmente por el nuevo trabajo.
Se confirma un fenómeno que recibe el pomposo nombre de régimen último asintótico (asymptotic ultimate regime) de la turbulencia. El artículo es Xiaojue Zhu, Ruben A. Verschoof, …, Detlef Lohse, «Wall roughness induces asymptotic ultimate turbulence,» Nature Physics (12 Feb 2018), doi: 10.1038/s41567-017-0034-3, arXiv:1802.04356 [physics.flu-dyn];más información divulgativa en Alexander J. Smits, «Ultimate evidence for the ultimate regime,» Nature Physics (12 Feb 2018), doi: 10.1038/s41567-017-0034-3.
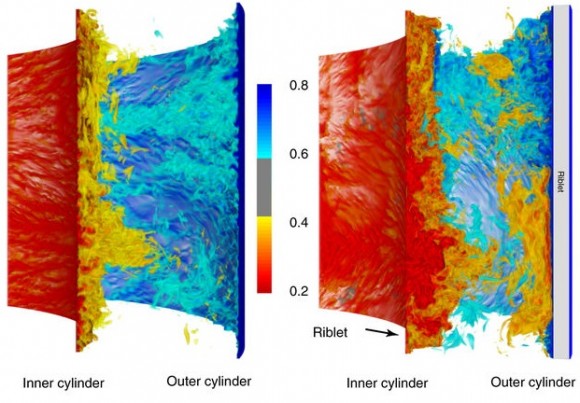
El nuevo artículo combina simulaciones numéricas directas (DNS) con resultados experimentales de laboratorio (EXP) para el problema de Taylor–Couette. Se han considerado cuatro casos en función de la rugosidad de las paredes interiores de los cilindros: SS, SR, RS y RR, donde la primera (segunda) letra describe el cilindro interior (exterior) y se usa la R para pared rugosa y S para la pared lisa. El cilindro interior tiene un radio de ri = 20 cm y el exterior de ro = 27,94 cm; su velocidades máximas de rotación son ωi = 7,5 Hz y ωo = 5 Hz, que corresponden a números de Reynolds máximos de Rei = 7,5 × 105 y Reo = 7,0 × 105. La pared rugosa se simula con entre 1 y 192 pilares empotrados (riblets) equidistantes con un altura de hasta el 10% de la anchura entre cilindros.
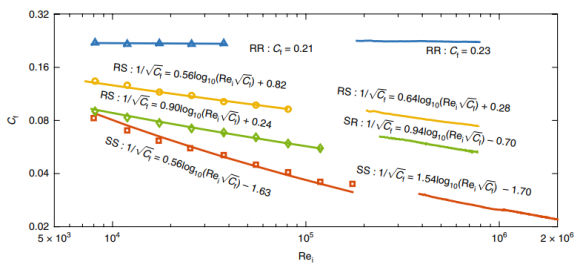
Esta figura muestra cómo depende el coeficiente de fricción con respecto al número de Reynolds para el flujo cercano al cilindro interior para las simulaciones numéricas (DNS, línea continua con símbolos a la izquierda) y para los experimentos de laboratorio (EXP, línea continua sin símbolos a la derecha). Los resultados para cilindros rugosos se han obtenido con 6 riblets por pared con una altura del 7,5% del hueco entre cilindros; los colores corresponden a RR (azul), RS (amarillo), SR (verde) y SS (rojo). Para ambas paredes rugosas (RR, azul) se confirma la predicción de Kraichnan de que el coeficiente de fricción es constante y no depende del número de Reynolds.
El efecto del tamaño de los riblets (desde el 1,5% al 10% de la separación entre ambos cilindros) se ilustra en esta figura (DNS a la izquierda con puntos coloreados y EXP a la derecha con línea continua de color). Se observa el régimen último de Kraichnan por encima del 5% (color morado). El artículo propone una descripción del flujo turbulento basado en una suma de leyes de potencia para la relación entre el número de Nusselt equivalente (Nuω) y el número de Taylor (Ta), en concreto, Nuω = a Ta0,38 + b Ta0,5, con los coeficientes a y b dependiendo de la rugosidad de las paredes. Confieso que no me agrada esta idea.
En resumen, sin entrar en más detalles técnicos, lo más importante es que la confirmación de la predicción de Kraichnan podría ayudar a entender mejor los flujos turbulentos en geofísica, meteorología, oceanografía y en la industria. De hecho, hay que recordar que la turbulencia tiene muchas aplicaciones industriales, como intercambiadores de calor, cámaras de combustión, reactores químicos, flujo en tuberías, etc. Y, además, en muchas de estas aplicaciones se fuerza la turbulencia mediante paredes rugosas.