«Piedra, papel o tijera» es un juego infantil de manos en el que la piedra vence a las tijeras rompiéndolas, las tijeras vencen al papel cortándolo y el papel vence a la piedra envolviéndola. Este juego ha sido muy estudiado en teoría de juegos porque ejemplifica los sistemas en los que tres estados se dominan mutuamente de forma cíclica. La dinámica de este juego y la de sus modelos en tiempo continuo es muy interesante (ver por ejemplo las pp. 171-188 de la ref. [1]). Sus aplicaciones son muchas en campos tan diversos como la ecología y la física de los procesos fuera de equilibrio. En ecología los sistemas dominantes cíclicos permiten entender la biodiversidad gracias a la coevolución mutua. En el modelo «piedra, papel o tijera» las poblaciones de tres especies oscilan gracias a su interacción mutua (May y Leonard ya lo estudiaron en 1975) y hay evidencia empírica de su validez (por ejemplo en comunidades de zorros y en poblaciones de cepas de la bacteria E. coli). El modelo (en tiempo) discreto tiene análogos continuos, dados por ecuaciones diferenciales ordinarias y estocásticas, y modelos espaciotemporales, ecuaciones en derivadas parciales, que permiten estudiar la generación de patrones de distribución espacial y el efecto de la migración de especies. Un asunto poco estudiado es el efecto de una tasa de mutaciones finita en la coevolución de las poblaciones modeladas por el juego «piedra, papel o tijera,» que estudia con cierto detalle un artículo reciente de Mauro Mobilia, de la Universidad de Leeds, Gran Bretaña [2]. Los interesados en dinámica no lineal de sistemas tienen un ejemplo bonito de sistema que presenta una bifurcación de Hopf de codimensión dos (con dos parámetros).
[1] György Szabó, Gábor Fáth, «Evolutionary games on graphs,» Physics Reports 446: 97–216, 2007. [copia gratis]
[2] Mauro Mobilia, «Oscillatory Dynamics in Rock-Paper-Scissors Games with Mutations,» ArXiv, 28 Dec. 2009.
Mobilia estudia un modelo en tiempo continuo del juego «piedra, papel o tijera» que utiliza el siguiente sistema de tres ecuaciones diferenciales acopladas
,
,
,
que presenta dos parámetros y
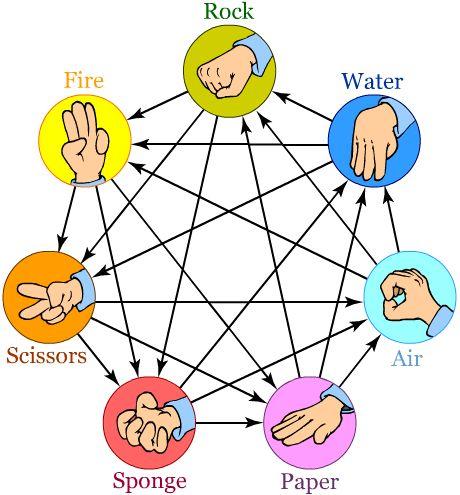
adimensionales. El primero es el valor de la recompensa negativa, lo que se pierde cuando se pierde el juego en cada jugada, relativo a una recompensa positiva de +1 (el juego será de suma cero si la recompensa negativa iguala a la positiva), y el segundo es la tasa de mutaciones, la probabilidad de que un individuo cambie de «especie.» Este sistema dinámico presenta 4 puntos de equilibrio, los tres estados absorbentes (1, 0, 0), (0, 1, 0) y (0, 0, 1), y un punto en el interior (igual a (1/3, 1/3, 1/3) cuando el juego es de suma cero). En función de los dos parámetros del sistema dinámico se observa comportamiento oscilatorio de tipo ciclo límite (cuando el punto fijo interior es un nodo inestable) o comportamiento oscilatorio amortiguado (cuando el punto fijo interior es un nodo estable). En el plano dado por los dos parámetros del sistema, una curva de bifurcación separa ambos comportamientos. El artículo de Mobilia además del comportamiento determinista de este sistema también estudia su comportamiento estocástico bajo la hipótesis de que las mutaciones se producen de forma aleatoria. En resumen, un bonito ejemplo para cursos de dinámica no lineal, bifurcaciones y caos (como el que yo he impartido en más de una ocasión), que disfrutarán los lectores de este blog más aficionados a la matemática aplicada y a la ecología de poblaciones. Para los demás, me gustaría indicaros que hay versiones del juego de manos «piedra, papel o tijera» un pelín más complicadas, ideales para frikis, por ejemplo, con 7 posibilidades como las mostradas abajo. La flecha indica la dominancia entre las diferentes posibilidades (visto en Lobotomizados, «Piedra Papel Tijera 2.0,» 19 de julio de 2007).