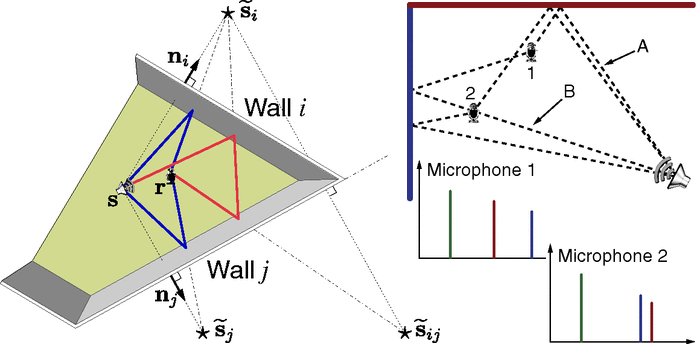
Se publica en PNAS la solución a un problema clásico en acústica, cuántos micrófonos son necesarios para oír la forma de una habitación tridimensional utilizando los sonidos generados por un altavoz. La respuesta es al menos cuatro (con probabilidad uno y para una habitación poliédrica convexa). Como los autores del artículo son de la Escuela Politécnica Federal de Lausana, Suiza, han ilustrado su algoritmo con la Catedral de Lausana. Los sonidos se reflejan en las paredes y forman ecos que son recogidos por los micrófonos y etiquetados por el nuevo algoritmo, lo que permiten reconstruir la forma tridimensional de la habitación. Se necesitan al menos cuatro micrófonos porque con menos pueden aparecer «ecos fantasmas» que parecen provenir de una pared «fantasma» (que no existe). Quizás pienses que es más fácil ver la forma tridimensional de la habitación que oírla, pero la técnica permite detectar objetos o personas en movimiento dentro de la habitación, luego si se usan ultrasonidos puede tener aplicaciones prácticas muy curiosas. Por supuesto, lo más interesante del trabajo técnico es la demostración matemática y el algoritmo desarrollado, que se basan en álgebra lineal y será disfrutado por muchos matemáticos. Nos lo ha contado Mark D. Plumbley, «Hearing the shape of a room,» PNAS 110: 12162–12163, 23 Jul 2013, que se hace eco del artículo técnico de Ivan Dokmanić, Reza Parhizkar, Andreas Walther, Yue M. Lu, Martin Vetterli, «Acoustic echoes reveal room shape,» PNAS 110: 12186-12191, 23 Jul 2013.
¿Por qué no bastan tres micrófonos? La razón son las soluciones isoespectrales, es decir, el hecho de que hay múltiples soluciones al problema y pueden aparecer formas «fantasmas» que generan los mismos ecos en los micrófonos. Un problema similar en dos dimensiones, cómo oír la forma de un tambor, ya apareció en este blog en «Es imposible reconocer la forma de un tambor escuchando sólo su sonido (cosas de la televisión),» 11 Jul 2008, y «Atención, pregunta, ¿se pude oir la forma de un tambor?,» 24 Ene 2011.
No quiero entrar en los detalles matemáticos de la demostración, ni en los del algoritmo de reconstrucción. Sólo destacaré que el nuevo resultado es verdad con probabilidad uno, lo que en matemáticas no es lo mismo que ser verdad, pero en la práctica no hay diferencia.
El nuevo trabajo tiene aplicaciones en realidad virtual, auralización, acústica arquitectónica e incluso en análisis forense de audio para la policía científica. Se puede utilizar para diseñar espacios acústicos con ciertas características o para cambiar la percepción auditiva de los espacios existentes. Con esta técnica se podría determinar la posición de una persona que camina por la sala y habla por un teléfono móvil. Sólo la imaginación limita las posibles aplicaciones.




Hola, Hola… uno, dos, tres, cuatro… probando..
¿Y si la sala es anecoica?
Interesante artículo. Con unos colchones baratos seguro que no se oiria nada.