Contar todas las partículas (fundamentales) conocidas es un ejercicio fácil. Las partículas son excitaciones localizadas de campos cuánticos, por lo que parece mejor contar las componentes de dichos campos. También es fácil, aunque hay algunas sutilezas que hay que tener en cuenta. En Twitter, Amarashiki (TSOR) y Alejandro Rivero (@arivero,web) realizaron este ejercicio hace unos días; por cierto, incluyeron al gravitón, una hipotética partícula aún no descubierta (que la mayoría de los físicos creemos que tiene que existir). Seguir los cálculos en Twitter es engorroso, por ello los resumiré en esta entrada. Además, incluiré algunos comentarios adicionales que ellos no han realizado de forma explícita, pero que me parecen interesantes.
Las partículas conocidas son de dos tipos, fermiones (espín 1/2) y bosones (espín 0, 1 y 2); incluyo el gravitón (espín 2), pero no el gravitino (espín 3/2), siendo ambas partículas hipotéticas aún no descubiertas, porque hay evidencia indirecta de la existencia de las ondas gravitatorias, pero no la hay de la supersimetría. Empezaremos contando los fermiones.
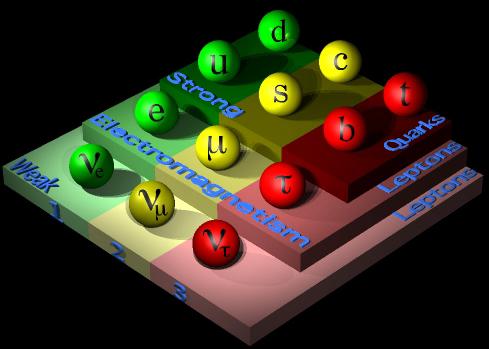
Como muestra la figura de arriba, los fermiones se dividen en tres generaciones de leptones y quarks; en cada generación hay dos leptones, uno cargado (tipo electrón) y otro neutro (tipo neutrino), y hay dos quarks, uno tipo arriba y el otro tipo abajo. Los tres leptones cargados (electrón, muón y tauón) tienen asociado cada uno un neutrino; los seis quarks son llamados arriba, u (up), abajo, d (down), extraño, s (strange), encanto, c (charm), fondo, b (bottom), y cima, t (top). La figura de arriba muestra 12 bolitas que corresponden a 12 partículas (aunque faltan sus correspondientes 12 antipartículas). Sin embargo, hay que recordar que los quarks tienen carga de color (con tres valores posibles), luego en lugar de 6 quarks tenemos 18 (y sus correspondientes 18 antiquarks). Por tanto, un cálculo naïve (ingenuo) nos dice que hay 24 fermiones y 24 antifermiones, un total de 48 partículas.
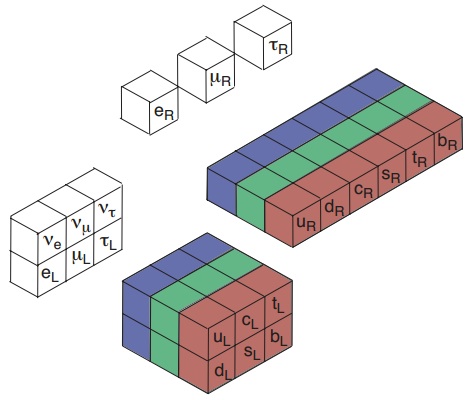
El cálculo anterior del número de fermiones no tiene en cuenta la quiralidad del modelo estándar. Sabemos que hay electrones levógiros (izquierdos, L) y dextrógiros (derechos, R), pero sólo hemos observado neutrinos levógiros. De hecho, las componentes levógiras se agrupan en parejas (dobletes), pero las dextrógiras no se emparejan (singletes). Por todo ello es mucho mejor contar el número de componentes de los campos que el número de partículas.
Un fermión de Dirac tiene cuatro componentes agrupadas en dos parejas, una pareja representa la partícula y la otra su antipartícula; en cada pareja hay una componente levógira y otra dextrógira. Los tres leptones cargados y los 18 quarks son campos fermiónicos de Dirac y cada uno tiene cuatro componentes. Sin embargo, no sabemos si los leptones neutros (neutrinos) son fermiones de Dirac (los neutrinos dextrógiros no han sido observados en los experimentos) o de Majorana (un fermión de Majorana tiene sólo dos componentes y es idéntico a su antipartícula); si todo va bien con los nuevos experimentos en curso, en un par de años deberíamos saberlo. Por tanto, si los neutrinos son fermiones de Dirac tenemos 4 × 18 + 4 × 3 + 4 × 3 = 96 componentes de campos fermiónicos (de las que 6 aún no han sido observadas en los experimentos), y si son fermiones de Majorana tenemos 4 × 18 + 4 × 3 + 2 × 3 = 90 componentes (siendo los neutrinos y los antineutrinos la misma partícula).
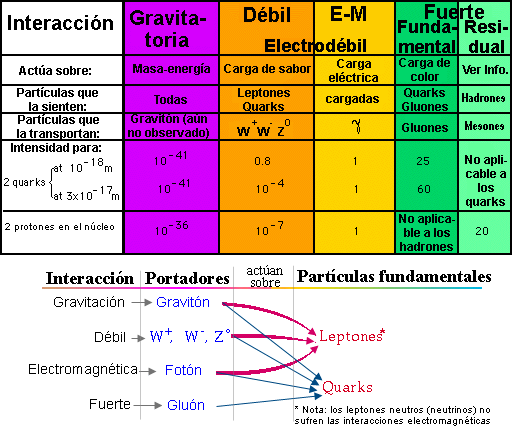
Ahora le toca el turno a los bosones. A baja energía, tras la rotura espontánea de la simetría electrodébil, tenemos un bosón escalar (espín cero), el bosón de Higgs, doce bosones vectoriales (espín uno), el fotón, los bosones Z, W− y W+, y 8 gluones, y creemos que existe un bosón tensorial (espín dos), el gravitón, aún no observado de forma directa. En total tenemos 13 bosones; no hay que contar las antipartículas porque todos los bosones que son neutros son idénticos a su antipartícula, y la antipartícula del W− es el W+, y viceversa.
Contemos ahora el número de componentes de los bosones. El campo de un bosón escalar neutro (como el Higgs) tiene una sola componente (y por ello es idéntico a su antipartícula); los bosones escalares cargados (como los Higgs predichos por la supersimetría) tienen dos componentes (el de carga positiva es la antipartícula del de carga negativa y viceversa). Por tanto, el Higgs del modelo estándar cuenta como una sola componente.
El campo de un bosón vectorial sin masa (como el fotón y el gluón) tiene dos componentes (transversales al momento) y el de un bosón vectorial con masa (como los bosones W y Z) tiene tres componentes (dos transversales y una longitudinal). Por tanto, en el modelo estándar tenemos 2 + 8 × 2 + 3 × 3 = 27 componentes de campos vectoriales.
El gravitón es un bosón de espín dos sin masa y por tanto tiene dos componentes (que son transversales al momento). Un gravitón con masa tiene cinco componentes (llamadas polarizaciones) ya que es un bosón de espín dos. Esto último puede resultar sorprendente a algunos lectores, pero se sabe desde el artículo de Fierz y Pauli (1939); el tensor métrico en cuatro dimensiones es simétrico, luego tiene 10 componentes, pero no son linealmente independientes entre sí, ya que se cumplen las identidades de Bianchi, que eliminan cuatro componentes, y la física cuántica requiere que su traza sea nula, lo que elimina una componente más.
Por cierto, Boulware y Deser (1972) afirmaron que las ecuaciones de un gravitón masivo deben incluir un término no lineal que invalida la condición de traza nula, con lo que el gravitón masivo debería tener seis componentes (o polarizaciones); pero según el único candidato firme a teoría cuántica de la gravedad, la teoría de cuerdas, el gravitón tiene cinco componentes. Finalmente, como nos recordó Amarashiki en Twitter, en D dimensiones el tensor métrico (una matriz real simétrica) tiene D(D+1)/2 componentes independientes, el campo de un gravitón sin masa tiene D(D−3)/2 componentes y el de un gravitón masivo D(D−1)/2 − 1; por ejemplo, en D=11 dimensiones el campo de un gravitón sin masa tiene 44 componentes.
Resumiendo el número de componentes de los campos bosónicos conocidos es de 1+27+2 = 30. Siendo el número total de componentes (fermiónicas y bosónicas) es de 126. Este número puede ocultar alguna simetría (como proponen Alejandro Rivero y muchos otros físicos), o bien puede ser una simple casualidad. Me permito argumentar a favor de esta última idea.
En cuanto al número de fermiones, no tenemos ningún argumento físico razonable que explique por qué hay sólo tres generaciones de partículas. Por ello, en los experimentos del LHC se siguen buscando partículas de una posible cuarta generación (como también se buscaron en Tevatrón y en LEP). Sin embargo, hay poca esperanza de encontrarlas. Sabemos que el neutrino de la cuarta generación debe tener una masa mayor de 45 GeV, luego será un neutrino muy diferente a los otros tres. Los tests de precisión electrodébil apuntan a la diferencia de masa entre la pareja de quarks de cuarta generación sea pequeña, menor que la masa del bosón W, m(t’) − m(b’) < m(W), con lo que sus desintegraciones más probables son t’→Wb y b’→tW, en las que han sido buscados sin éxito reultando m(t’)>650 GeV y m(b’)>660 GeV ambos al 95% CL (Andrew Ivanov (ATLAS, CMS), «Limits on Fourth Generation Fermions,» arXiv:1308.3084, Subm. 14 Agu 2013). Finalmente, el estudio de los canales de desintegración del Higgs también descarta una cuarta generación de quarks con masas menores de de unos 650 GeV.
Tampoco sabemos si existen o no nuevos bosones vectoriales neutros, Z’ (Z-prima), o cargados, W’ (W-prima), que corresponderían a nuevas simetrías U(1) y SU(2), respectivamente, a incorporar al modelo estándar. Las búsquedas de estos bosones en el LHC los descartan con masas inferiores a 1 TeV (en algunos canales de búsqueda de hasta 2 TeV). Tampoco sabemos si existen nuevos bosones escalares (nuevos bosones de Higgs). Y no he mencionado la posibilidad de partículas más exóticas.
Sólo hemos explorado el modelo estándar por debajo de un 1 TeV (y todavía no de forma completa). En mi opinión, como la de muchos físicos, pensar que lo que hemos descubierto hasta ahora es lo único que existe es muy discutible. Otra cosa muy diferente es que dichos descubrimientos estén a la vuelta de la esquina. Acabamos de iniciar el siglo XXI y todavía no hemos completado el modelo estándar (aún no conocemos muchas de las propiedades de los neutrinos y hay muchas predicciones del modelo estándar que aún no han sido verificadas). Hay que darle tiempo al tiempo. Pero con toda seguridad habrá sorpresas, aunque no sé si llegaré a verlas en la primera mitad del siglo XXI.
PS: Esta entrada ya no admite comentarios. 22 agosto 2013 2:00 am



«Hay que darle tiempo al tiempo. Pero con toda seguridad habrá sorpresas, aunque no sé si llegaré a verlas en la primera mitad del siglo XXI»
Francis con todos los respetos, como divulgador eres extraordinario pero como «aguafiestas» tampoco tienes precio 😀
Decir que no vamos a ver nada nuevo en 37 años es ser demasiado conservador, en mi opinión por los siguientes motivos:
1º) El LHC comenzará a funcionar al doble de energía en 2015, con 13 o 14 TeV en el centro de masas por lo que la luminosidad se incrementará enormemente. Además futuras mejoras en el mismo podrían incrementar la energía de funcionamiento hasta 30 TeV en el plazo de 25 años.
Además de la posibilidad de encontrar nuevas partículas esto aumentará la posibilidad de ver fenómenos que indiquen física BSM como la anomalía de los mesones Bs.
2º) El año que viene la versión mejorada de Ligo empezará a funcionar con lo que es posible que se anuncie el descubrimiento de las ondas gravitatorias en el plazo de pocos años. También el año que viene Planck puede anunciar la detección de ondas gravitatorias primordiales.
3º) Los experimentos de materia oscura deben acotar enormemente la búsqueda, en pocos años debemos ser capaces de detectarla si es una WIMP de baja o media energía. Incluso podría ser una partícula supersimétrica tan ligera como 8,6 GeV que es la energía que apunta la búsqueda de CDMS II y otros experimentos.
4º) Los nuevos experimentos en marcha y los futuros (Planck, experimentos con neutrinos, experimentos de precisión, medidas cosmológicas o astrofísicas, desintegración de protones, medidas de la gravedad a corta escala, etc, etc) pueden aportar pistas experimentales que nos guíen en la dirección correcta.
5º) Las mejoras tecnológicas (software, simulaciones de Montecarlo, hardware, etc) deberán multiplicar nuestras posibilidades de búsqueda.
6º) Nuevos desarrollos teóricos pueden en cualquier momento entrar en escena con soluciones a los problemas de los esquemas actuales e incluso nuevas predicciones experimentales.
7º) Partículas de baja energía como los Axiones pueden ser detectadas con instrumentos de precisión mejorada.
Y seguro que me dejo más cosas…
Planck, yo tengo un sueño, veré nueva física, pero quizás sólo es un sueño.
Yo también (tanto experimentalmente como explicación). El «sueño» de una noche verano… Por cierto Francis, matización sobre una frase que has dicho (puedo equivocarme como todos). Dices:
«(…)el tensor métrico en cuatro dimensiones es simétrico, luego tiene 10 componentes, pero no son linealmente independientes entre sí, ya que la condición de energía positiva requiere que se cumplan las identidades de Bianchi(…)»
Que yo sepa, el que se cumplan las identidades de Bianchi no depende para nada de la condición de energía sobre el tensor energía momento. Quizás no estamos hablando de lo mismo. Aclaremos esa frase. Las identidades de Bianchi (hasta donde yo creo comprender), en Relatividad General, aparecen como consecuencia de la simetría «gauge» (en el sentido del segundo teorema de Noether) dada por la covarianza general de la teoría. Puedo estar equivocado, no quiero parecer «sabelotodo» ni pedante, sin embargo. La condición de energía positiva en relatividad general es una condición que (creo) no tiene nada que ver con las identidades de Bianchi.
Gracias, Amarashiki, tienes razón (no sé por qué me vino a la memoria que la identidad de Bianchi era clave en la demostración de Witten del teorema de energía positiva). Lo cambio.
En el apartado de «experimentos de precisión» ya hay uno que es prometedor, en el momento magnético del muón.
Planck. Te comento:
1) No sé si es ser aguafiestas o no, pero hay que aceptar de momento el escenario «pesimista» o «conservador» (algunas veces tildado de «pesadilla», aunque lo que es pesadilla o sueño es subjetico) de que existen posibilidades reales de que el LHC a plena energía no descubra ninguna otra partícula o campo nuevo a 14 TeV. Me gustaría estar equivocado, claro. Pero de momento, a 8 TeV y «baja luminosidad» eso sí, hemos visto sólo física del quark top (por cierto Francis, deberías hacer una entrada sobre el artículo de ayer, que creo citaba dorigo en su blog, sobre la medida de la anchura y por tanto el tiempo de vida del quark top con mayor precisión hasta la fecha; 8 órdenes de magnitud solamente alejado, en tiempo, del tiempo de Planck, $$latex 10^{-33}s$$) y física del «Higgs»-like field de unos 127GeV. Desde luego, podemos ponernos en modo «superoptimista» como Lubos Motl en su blog, y decir que a 14 TeV, con 6 TeV más y el salto de luminosidad, eso va a producir una plétora de nuevas partículas. Pero creo que es momento de aceptar que es muy complicado tal escenario. No digo que no puedan encontrarse (por ahí andan mis esperanzas) algo como el esfalerón, un monopolo electrodébil o clases exóticas de partículas compuestas por «moléculas de quarks», tal vez incluso algún tipo de fenómeno ligado a física del SM. Pero ha llegado la hora de la verdad para la «nueva física en el LHC». El indicio teórico de que la situación es «crítica» es que muchos ya están moviendo las escalas de energía fuera del alcance del LHC. Y esto no es ser aguafiestas, es simplemente observar las cotas y que da LHC, ver lo que las teorías dicen, y «obrar en consecuencia». Ojalá no fuera así, pero es la Naturaleza y no nosotros la que decide.
2) Sobre LIGO. Sean Carroll me comentó y lo ha dicho también públicamente en su blog, que espera ver ondas gravitacionales en su time-life, e idealmente en menos de 10 años. Además la mejora de la sensibilidad por el uso (creo) de la técnica de «squeezing» en los láseres va a producir un salto enorme en este experimento.
3) Soy más escéptico sobre la materia oscura. Una de las cosas que hay que entender antes para varios experimentos de detección directa es la contribución del scattering coherente neutro de neutrino-núcleo, cuya sección eficaz es una predicción aún no confirmada del Modelo Estándar (siendo burdos, esta sección eficaz es proporcional al cuadrado de la constante de Fermi). Este proceso es importante porque puede producir una identificación errónea de materia oscura cuando se observa el «recoil» o retroceso de los núcleos en dichos experimentos (creo entenderlo). Es muy posible que la materia oscura, sea lo que sea, es «ligera» o superpesada o con unos acoplos «fine-tuned» que la hace inaccesible fácilmente, pero el hecho de no encontrar evidencias firmes de ella, me hace sospechar si estamos «olvidando algo». ¿MOND? Tal vez no…O tal vez, como apuntan ya algunos, y yo en particular he comentado en varios sitios, MOND/MOG y Cold Dark Matter son simplemente aspectos complementarios de una misma «física» desconocida. Ya contaré algo más de esto en mi blog cuando lo retome el mes que viene. Wilczek aún sigue pensando en el axión como «solución» mínima a DM, y creo que es una persona con peso para saber lo que dice (otra cosa es que ahora también se ponga a hablar de Multiversos, jejeje).
4) Estoy de acuerdo. Y creo que en el área de la astronomía de neutrinos, y la física de neutrinos podremos encontrar sorpresas con más facilidad. Además están esos rayos cósmicos misteriosos que no entedemos aún…
5) La computación cuántica, si se hace realidad, puede darnos una herramienta poderosa para simular nuestros modelos. Y espero que con superordenadores, mejoren en los próximos años, por ejemplo, la comprensión del espectro de teorías en el retículo (ya se hace, de hecho). También serán importantes para comprender vía simulación el comportamiento de fases exóticas de la materia.
6) De acuerdo.
7) Los axiones son la principal apuesta de Wilczek. De hecho, ahora que hemos encontrado «el Higgs» (sea lo que sea éste), el axión es (junto quizás a los neutrinos superpesados) la partícula cuyo espacio de parámetros (acoplo y masa) está más constreñido por todo tipo de experimentos. En comparación, el espacio de parámetros de SUSY en el MSSM y otras extensiones del Modelo Estándar está mucho más «abierto».
Sobre la cuenta de partículas (que me interesa a mí más, inicialmente, que la de componentes independientes de los campos) voy a hacer un resumen yo también aquí (puedes incluirlo si quieres en tu post) en el Modelo Estándar+gravedad (Relatividad General)
A) Fermiones ( u,d,c,s,b,t, e, $latex mu$, $latex tau$, $latex nu_e, nu_mu, nu_tau$)
-> Caso a) 24 fermiones y 24 antifermiones (sin contar quiralidad)= 48 partículas distintas. Razón: (número de quarks)x(color)= 6×3= 18.(número de leptones)=6. Total 18+6=24 más antipartículas (si éstas son diferentes, suponiendo que todos son fermiones Dirac; esto está claro para los quarks, pero aún NO sabemos el carácter espinorial de los neutrinos). Si los neutrinos fueran idénticos a sus antipartículas, hemos sobrecontado los neutrinos. Si éstos son Majorana, la cuenta sería (ni me estoy equivocado) 18×2+3×2+3×1=45 partículas, 24 fermiones, de los que 3 son idénticos a sus antifermiones. En resumen:
a1) Si el neutrino es Dirac, en el SM hay 48 partículas tipo fermión/antifermión en el SM.
a2) Si el neutrino es Majorana, en el SM hay 45 partículas tipo fermión/antifermión en el SM.
->Caso b) Contando color Y quiralidad (R/L componentes) sólo para leptones cargados. Tenemos, en el SM,
(número de quarks)x(color)x(quiralidad)=6x3x2=36. La cuenta con leptones es más divertida, pues hay que diferenciar a los cargados de los neutrinos. Para los cargados, que son dobletes, tenemos que (leptones cargados)x(quiralidad)=3×2=6. Para los neutrinos, que en el SM son singletes, tenemos que (neutrinos)x (quiralidad left only)=3×1=3. Total 9 fermiones. Contamos antipartículas. Si el neutrino es Dirac como los leptones cargados, 9×2=18 partículas en total distintas. Si el neutrinos es Majorana, 6×2+3×1=15 partículas distintas. En resumen, incluyendo quiralidad y color:
b1) Si el neutrino es Dirac, en el SM hay 36+18= 54 partículas tipo fermión/antifermión.
b2) Si el neutrino es Majorana, en el SM hay 36+15=48 partículas tipo fermión/antifermión.
->Caso c) (Extra «más alla del Modelo Estándar») Extensión mínima por simetría de quiralidad $latex nu SM$ tipo Shaposnikov del SM. Supongamos que existen componentes de quiralidad «superpesadas» del neutrino de tipo Right, y cuya existencia hasta el momento ha pasado desaperciba. La idea de Shaposhnikov es completar y «simetrizar» el SM bajo quiralidad en la parte de los neutrinos. En términos técnicos, el lagrangiano del $latex nu SM$ es algo del tipo siguiente:
$latex mathcal{L}=mathcal{L}_{SM}+ibar{N}_Apartial_mu gamma^mu N_A -(F_{alpha A}bar L_{alpha}N_Atilde{phi}-dfrac{M_A}{2}bar{N}^c_AN_A+ h.c.)$
y donde $latex F$ son los acoplos de Yukawa, L los dobletes de leptones left-handed (izquierdos), alfa indica la generación ($latex e,mu,tau$), $latex phi$ es un doblete de Higgs y los neutrinos right-handed (diestros) denotados por $latex N_A$ tienen carga eléctrica cero, carga débil cero, y carga fuerte cero (esto es son neutros bajo el grupo del Modelo Estándar porque no tiene ni carga eléctrica, ni «carga débil», ni carga de color).
Este modelo «completa» mínima mente el SM bajo quiralidad, de forma que en la cuenta de arriba incluimos el factor ahora 2 de quiralidad. Y de nuevo rehago las cuentas:
(número de quarks)x(color)x(quiralidad)=6x3x2=36. La cuenta con leptones es más divertida de nuevo, pues hay que diferenciar a los cargados de los neutrinos como hice antes. Para los cargados, que son dobletes, tenemos que (leptones cargados)x(quiralidad)=3×2=6. Para los neutrinos, que en el SM tienen ahora quiralidad, tenemos que (neutrinos)x (quiralidad left y right)=3×2=6. Total 12 fermiones. Contamos antipartículas. Si el neutrino es Dirac como los leptones cargados, 12×2=24 partículas en total distintas. Si el neutrinos es Majorana, 6×2+6×1=18 partículas distintas. En resumen, incluyendo quiralidad y colo en el sector quark y leptones, y también distinguiendo el caso de Dirac/Majorana), en el modelo de Shaposhnikov tenermos:
3a) Neutrino Dirac. 36×2+12×2=72+24=96 partículas distintas. (48×2)
3b) Neutrino Majorana 36×2+18=72+18=90 partículas distintas. (45×2)
B) Bosones (1 fotón, 8 gluones, bosones vectoriales intermedios $latex W^-,W^+, Z$, Higgs mínimo h, gravitón)= 14 (te olvidaste en la cuenta de incluir a tu partícula favorita, el Higgs ¡! :D). Supongamos que el higgs es realmente «único» y un singlete. Para todo en los 3 casos anteriores, y que también el gravitón es neutro en color, carga débil, color, y carga eléctrica.
C) Suma total. Entonces, el número total de partículas en los casos anteriores es la siguiente.
Modelo Estándar:
a1) 48+14= 62 partículas
a2) 45+14= 59 partículas
b1) 54+14= 68 partículas
b2) 48+14= 62 partículas
Modelo de Shaposhnikov (más allá del Modelo Estándar):
c1) 96+14= 110 partículas
c2) 90+14= 104 partículas
Y esto sólamente sin contar mesones y bariones compuestos de quarks, sólo a nivel de partículas «elementales». En comparación, la Tabla Periódica contiene actualmente 118 «elementos» químicos.
Indicación, si me he equivocado en alguna cuenta, me indicádmelo.
Una cosa que me llama la atención de la filosofia de simplificar la cuenta es que en el lado de los fermiones tendemos a aplicar particula=multiplete, por ejemplo el quark top para los tres estados de SU(3) color, o el lepton zurdo para los dos estados neutrino y electron de SU(2) debil, y asi hasta que en una hipotetica unificacion GUT tendriamos solo una particula. En cambio en el lado bosonico no solemos actuar asi, y siempre pensamos en ocho gluones, nunca en un unico gluon. Esto ya sin entrar en considerar el lio de si queremos contar autoestados de masa o autoestados de «carga».
Para los fermiones y spinores, es que hay mucha más riqueza que para las partículas de espín entero (ni nos restringimos a teorías gauge tipo YM o Relatividad General, por ejemplo), además que hay que tener más cuidado con ellos contando componentes.
Me explico, con un espinor podemos ademas de estudiar cómo se comporta por simetría de carga y ver su diferencia con su respectiva antipartícula, podemos proyectarlo en componentes quirales con $latex gamma_5$ por el método usual, esto es, usando los proyectores $latex (1pm gamma_5)/2$ o sus análogos en otras dimensiones. Es precisamente esta singularidad de los fermiones la que, históricamente, ponía en el brete a la SUGRA en D=11 por el «famoso» teorema «no-go» de que «no hay forma» de obtener una teoría «quiral» como el Modelo Estándar directamente desde 11 dimensiones. Este argumento es por supuesto particular, y los teoremos no-go, como ‘t Hooft ha mencionado alguna vez en algún sitio, se evita yendo a las «asunciones» e «hipótesis», y «relajándolas» un poco. Así pasó por ejemplo con SUSY. El teorema no-go que decía que no había forma de obtener el grupo de poincaré y el grupo del modelo estándar desde un mismo «grupo» se solucionó relajando la condición de grupo para permitir la introducción de generadores espinoriales. Así, en el contexto de los «supergrupos» sí que es posible tener un objeto cuya simetría se descompone en el grupo del SM y el grupo de Poincaré.
Con los bosones, al menos con los conocidos, hay menos libertad. Los fotones o los gluones son en cierto sentido sus propias antipartículas (en el caso del fotón y del gluón, e incluso, posiblemente del gravitón), mientras que el Z y los W son especiales porque son masivos (ciertamente, no consideramos nunca componentes left of right de los W ó Z), y el higgs del Modelo Estándar es un mero singlete (que sepamos, habrá que ver qué pasa con ese higgs de 127GeV). Por tanto, con los bosones no distinguimos generalmente quiralidad, como sí lo hacemos con los fermiones. Ése, en mi opinión, es el punto. Shaposhnikov tiene charlas contando los bosones (sin el gravitón) del SM de forma diferente. Ejemplo, slides 35, 36, 37 y 38 de esta conocida charla suya:
chalonge.obspm.fr/Paris07_Shaposhnikov.pdf
Por eso, también, desde un punto de vista teórico, hay que «definir» lo que uno quiere decir al contar partículas (y antipartículas). Podemos hacer lo que comenta Francis, de contar grados de libertad, o podemos contar «partículas» como «elementos». Y tenemos que corregir la cuenta de fermiones que hemos hecho arriba, que no está bien del todo.
Francis: en tu cuenta del artículo (y en las que yo hice). Cuando cuentas los fermiones, también hemos incluido los antifermiones. Por eso decía yo que creo está mejor decir que hay 14 partículas de tipo bosón (incluyendo los anti de los W). Higgs neutro mínimo, el fotón, 8 gluones, W+, Z, gravitón (son 13), pero en la cuenta total de los bosones (como en la de los fermiones), hay que sumar el W-. Total 14 bosones (incluyendo partículas y antipartículas), o bien 13 si incluimos el gravitón (suponiendo exista).
En la cuenta que hace Shaposhnikov en la charla antedicha tanto para el Model Estándar como para su Modelo, se hace una mejor cuenta y cuenta estados o partículas de forma diferente. A saber, él «cuenta» de forma «mejor» (distinta) a lo que he hecho yo «arriba» (sí, algo «naive»), y hace algo más a lo que dice Alejandro, pues cuenta en primer lugar partículas en dobletes y singletes de quarks (para un total de 36, 18 left que se pueden agrupar en 9 dobletes, y 18 singletes R) y luego cuenta dobletes de fermiones «left»(L) y singletes de fermiones «right» (R) bajo el Modelo Estándar. Después cuenta estados leptónicos, que, en su forma de contar, son 9+3 estados leptónicos, que son 9 singletes por L/R más 3 dobletes¡!. Esta cuenta hay que explicarla mejor para entenderla. Porque no es el contaje que yo tenía en mente hace unos días. Además, que, curiosamente, en su modelo más allá del modelo estándar, Shaposhnikov también cuenta el mismo número de estados leptónicos 9+3 (creo que es una errata en la slide), debería decir 9+6 (creo), sólo cambia que aparecen 3 nuevos singletes o estados leptónicos, lo que cambia el contaje. Es decir, según Shaposhnikov (no distingue Dirac o Majorana en ningún caso) tenemos:
-Para el Modelo estándar 90 grados de libertad o «partículas» fermiónicas (incluyendo antipartículas).
-Para su extensión mínima $latex nu SM$ hay 96 grados de libertad fermiónicas.
-Para el Modelo Estándar y su modelo, sigue habiendo, según sus cuentas, (8+3+1)x2+4=28 bosones (contando partículas y antipartículas). Esto concuerda con nuetra cuenta arriba, incluyendo el higgs mínimo neutro, ya que tenemos 8×2=16 de los gluones (contando polarizaciones), 2 del fotón, 3×3=9 de los bosones masivos y 1 del higgs. 16+2+9+1= 28. Voilá.
En total:
-Para el modelo estándar (según la cuenta de Shaposhnikov) hay 90 fermiones/antifermiones+28(bosones/antibosones)=118 partículas elementales( casualidad que coinde que el número de elementos de la actual tabla periódica).
-Para el modelo de shaposhnikov hay 96(fermiones/antifermions)+28(bosones/antibosones)=124 partículas en total
Comentario: sí que parece importante contar la quiralidad (más bien la polarizazión) para contar «partículas» o estados de los bosones. Otra cosa distinta, es que en física de partículas, generalmente, no solemos hablar de las componentes transversales (y de la helicidad o bien de la quiralidad) de las partículas que son bosones.
Comentario (II): evidentemente no hay supersimetría evidente y manifiesta en el Modelo estándar porque el número de fermiones/antifermiones no es igual al de bosones/antibosones (aquí convoco a Alejandro para si con su numerología y cuentas es capaz de que cualquiera de los contajes que hemos hecho hasta ahora «matchee» los grados de libertad fermiónicos y bosónicos: no parece fácil).
Comentario (III): De las cuentas anteriores, parece que lo que nos faltan son «bosones», no fermiones para poder tener supersimetría. También, en el caso del contaje de shaposhnikov, no hemos contado la modificación que introduciría el hipotético gravitón sin masa, que da 2 estados o partículas/gravitones de diferente helicidad +2, -2. Incluir sólo dos grados de libertad bosónicos tampoco arregla las cuentas demasiado. Si creemos en SUSY, eso significa que faltan aún muchas cosas. Si no creemos en SUSY, esos significa que las partículas como las hemos contado son resultado de la combinación de subconstituyentes más simples (¿cuántos?¿por qué están tan ocultos?), y algo debería simplificar esta plétora de entidades elementales, que si contamos en total, son mayor que el número de elementos conocidos del actual Sistema Periódico.
Comentario (IV): Pregunta obvia. ¿Qué significa la aparente complejidad de la estructura fundamental de las partículas subatómicas? Visto de esta perspectiva, el zoológico de partículas elementales del Modelo Estándar (eso sin contar resonancias y moléculas de quarks, como los hadrones), es mayor que el número de átomos conocidos (y también átomos estables conocidos). ¿No debería una teoría más fundamental simplificar el número de entidades fundamentales? Es curioso que, en general, no parece así.
Una errata, antes del dibujo que has includo. Digo:
«(…)o bien 13 si incluimos el gravitón (suponiendo exista). » Eso está mal, evidentemente es 13 si EXCLUIMOS, el gravitón (y esto es sin contar polarizaciones, i.e., estados, distintos.
Todo esto prueba que el lenguaje de las partículas es sutil para contar. Normalmente, no contamos «polarizaciones» del fotón, o del W, como partículas distintas, sin embargo, sí contamos generalmente las proyecciones quirales de los fermiones y los dobletes como «estados» distintos.
El lenguaje de los supermultipletes en SUSY también es un poco lioso al principio. En particular cuando cambiamos de unas dimensiones a otras, … Más que las bestias de Alejandro con Dirac y Majorana, a mí lo que siempre me ha parecido más complicado es el asunto de «identificar» los «grados fundamentales» en una teoría que se reduce o compactifica.
Francis, corrígeme si me equivoco, tu opinas que lo importante son los campos y sus componentes.
¿Cómo sería una teoría con un sólo campo que se descompusiera en todos los conocidos? Me gustaría destacar que eso no ocurre en ninguna teoría supersimétrica, ni en SUGRA D=11 (y en M-theory). Si el campo «unitario» existe a una «muy alta energía», en todos los modelos hasta el momento no hay un una teoría con un sólo campo,o una única fuerza. Por ejemplo, en teoría M, hay varios campos, no sólo uno. Si la unificación de las fuerzas a alta energía existe, y el campo unitario también. M-theory, cuyos objetos fundamentales son 2-branas y 5-branas, tiene diferentes campos y sus interacciones, y su aproximación efectiva es SUGRA d=11, con sólo tres campos fundamentales, el elf-bein$latex E^A_M$ (con el que se construye la métrica de 11D $latex g_{AB}), el gravitino $latex psi_{M}^alpha$ y la 3-forma o campo tensorial antisimétrico con 3 índicas $latex A_{munusigma}$. En ese sentido, hay 3 campos en alta dimensión, no un único campo.
Witten dijo hace mucho que las teorías y leyes físicas se simplifican en dimensiones superiores (como en KK original, las versiones contemporáneas, o la propia supergravedad o M-theory). Pero desde luego aún no hay ninguna teoría en la que TODOS los campos que vemos en 4D surjan de un sólo campo en dimensión superior. ¿Se abandonó el KK original tal vez porque tampoco lograba acomodar los campos de materia que tenían que ser incorporados a parte en la teoría? Obviamente, supercuerdas usa KK PERO acomoda los fermiones via supersimetría, de forma que incorpora fermiones. Algo que NO puede hacer una teoría Kalula-Klein pura, a la que hay que acoplar materia a posteriori. ¿Tal vez la respuesta a por qué se abandonó KK original sólo con partículas, originalmente, tenga que ver con esto?
OPs. Una precisión la comunicación anterior. He dicho que los grados de libertad de M-theory son 2-branas y 5-branas. Sin embargo, los grados fundamentales de M-theory no se sabe con certidumbre cuáles son. Por dualidad desde sugra, M-theory tiene 2-branas y 5-branas (al menos) objetos fundamentales, pero no está claro cuál es fundamental. M-atrix theory usa D0-branas como entes fundamentales para la descripción de M-theory. Pero es sólo una conjetura.
El lagrangiano del $latex nu SM$ de Shaposhnikov debería salir como sigue:
$latex mathcal{L}=mathcal{L}_{SM}+ibar{N}_A partial_mu gamma^mu N_A -left(F_{alpha A}bar{L}_alpha N_A tilde{phi}-dfrac{M_A}{2}bar{N}_A^c N_A+h.c.right)$
La interpretación es simple: es un SM «extendido» mínimamente de forma que la simetría de quiralidad R/L sea explícita con el añadido de los neutrinos R (righthanded), superpesados en comparación al neutrino L del Modelo Estándar y sin carga bajo el grupo del Modelo Estándar, de forma que tanto quarks como leptones aparecen simétricos bajo L/R.
Hecho.
Gracias.
Quizas es porque el unico suspenso de mi carrera me lo pusó, practicamente en su lecho de muerte, el lider del grupo experimental de busqueda de neutrinos de Majorana en Zaragoza, pero el caso es me convence muchisimo más que tengamos neutrinos de Dirac. Aunque solo sea por el seesaw. Asi que me agarro a 96 y no 90 en la cuenta, y por ello prefiero el total de 126 contando el Higgs y el gravitón, o 124 sin el gravitón.
Lo del seesaw es esquizofrenico: queremos tener a la vez masa de Majorana y masa de Dirac. Pero bueno, parece que es la mejor idea.
En el guest post toqué la cuestion de como sigue la cuenta si intentamos añadir minimamente supersimetria. El famoso MSSM añade un campo de Higgs entero, otros cuatro bosones pues. Pero eso es porque queremos un mecanismo para generar masa y hay que hacerlo independientemente para el sector up y el sector down. Si nos olvidamos de la cuestion de los acoplos del higgs a fermiones y nos limitamos a mirar teoria de representaciones, estariamos en una situacion que yo llamo a secas el SSM, y que solo exige añadir dos bosones H+ y H- para que los supermultipletes de W+ y W- tengan cada uno cuatro componentes bosonicas (por cierto hay quien utiliza DOF, degrees of freedom, en vez de componentes, para referirse a esta cuenta).
En resumen, de componentes bosonicas+fermionicas, el MSSM sumaria 128+128 y el «SSM» 126+126. Añadiendo el graviton y el gravitino, «MSSM-sugra» tendria 130+130 y «SSM-sugra» 128+128.
Encontrar esos H+ y H- y no encontrar ninguna otra particula SUSY seria bastante curioso: significaria que para cada supermultiplete tendriamos la mitad de sus componentes; una situacion que ahora mismo tenemos ya en el lado de los quarks y leptones, pero no en el lado de gauge y higgs. Y por supuesto igual estariamos si aparacen A y el otro H0 y no aparece ningun higgsino. A ver si hay suerte y el LHC nos trae algo de esto.
Yo prefiero mucho más incidir sobre la aparente «singularidad» de los neutrinos para preferir que el neutrino sea Majorana. ¡Llamádme loco/crackpot! De hecho, el supervisor de mi tesina me comentó que el piensa que los neutrinos son Dirac, porque, según él, no hay nada que evite ajustar Yukawas supercanijos al neutrino y así explicar su pequeña masa. Obviamente, cualquier postura con respecto al neutrino, mientras no se resuelva la cuestión desde el punto experimental, parte de nuestros prejuicios teóricos. Mi supervisor, esencialmente, eludía el problema pequeña jerarquía (que según él, no es un problema, como tampoco, la el problema de la jerarquía), simplemente es una evidencia de diferentes escalas en las teorías. Con el Higgs, en el SM, los Yukawas son «free», y por tanto no hay problema en ajustarlos como se quiera (aunque por supuesto la pregunta de por qué a los neutrinos hay que ponerles Yukawas tan pequeños puede hacernos y nos hace protestar y pedir explicación, como lo hace el asunto de por qué la masa de planck es tan grande en comparación a la masa de los bosones electrodébiles o el propio higgs de 127GeV).
En mi caso, prefiero que el neutrino sea Majorana por diversos motivos:
1) Da candidatos mínimos a materia oscura sin introducir a priori supersimetría o el axión, en especial si hay componentes estériles.
2) Los neutrinos de Majorana son más fundamentales que los de Dirac (aunque esto puede ser simplemente subjetivo) a nivel de teoría de representaciones.
3) Con neutrinos de Majorana podemos construir términos de masa más generales en el lagrangiano (seesaw). Sobre la bestia que es un neutrino que posee términos de Dirac y Majorana, Alejandro, la clave es entender que hay un espinor «simétrico» que se divide en dos tipos de estados, «ligeros» y «pesados» (o superpesados).
En el fondo, es la misma pregunta (la bestia de la disparidad de masa entre los neutrinos L y R) que hay en teorías supersimétricas entre la masa de sus partículas y las spartículas¡! Las spartículas compañeras de los bosones y fermiones conocidos deben ser mucho más pesados que ellos, al menos según los resultados del TeVatron y ahora del LHC. El seesaw mechanism es algo que se intenta añadir a las teorías supersimétricas para explicar la disparidad de masas en algunos modelos (no soy experto, pero he oido hablar de los susy-seesaw).
Desde luego, para mí, uno de los problemas no resueltos más grandes de SUSY es cómo se rompe (sin generar una energía del vacío que NO sea gigantesca sino similar a la observada) y por qué razón las spartículas (suponiendo SUSY como postulado a nuestras teorías, significa la existencia de spartículas) son mucho más pesadas que las que hoy conocemos.
Recordemos que la masa de los neutrinos conocidos debe andar grosso modo en torno a los meV, o decenas de meV, mientras que los de los superpesados (o estériles) podrían ser de hasta keV. Los quarks tienen masa del orden GeV, salvo el top, que extrañamente es unos 173GeV. Los leptones tienen masas de 0.511 MeV, 106 MeV y 1777 MeV. Los W están en 80 GeV, los Z en 91, el Higgs en 127, y la masa de planck en $latex 10^{19}GeV$!!!!! Las cotas de LHC indican que cualquier nueva partícula está, grosso modo (excluyendo el axión y otras partículas con interacciones superdébiles que no podamos detectar) por encima de unos 500 GeV en general. Así que, ciertamente, hay una jerarquía entre las partículas del SM y SUSY. Lo de suponer que el gap entre SUSY y el sector electrodébil sea más grande o más pequeño es ciertamente un prejuicio: entre el electrón y el muón, hay un factor 200, y entre el electrón y el tau, hay un factor de orden 4000 (estoy redondeando en números redondos). ¿Podría SUSY esconderse no en la escala TeV sino bastante más allá? Ciertamente.
Tengo una duda:
«pero el caso es me convence muchisimo más que tengamos neutrinos de Dirac»
Como puede estar una particula fundamental descrita por un spinor de Dirac, que en cuatro dimensiones no es una representacion irreducible de Spin(1,3)? Yo pensaba que o bien se consideraban espinores de Weyl, o bien de Majorana (ambos son irreps), pero no de Dirac.
En efecto parte de la duda que tengo es la nomenclatura… ¿Como llamamos a una bestia que tiene los dos tipos de masa? Supongo que decir que es un par de Weyls es una salida socorrida.
Pero suponte que no tuvieramos ni neutrinos ni fuerza electrodebil, tan solo electrones, quarks, electromagnetismo y fuerza fuerte. Diriamos entonces que las particulas fundamentales son los espinores de Weyl? o que son particulas de Dirac?
Por cierto, que estaba pensando que esto, fuerte mas electromagnetismo, puede ser un ejercicio de Kaluza-Klein mas simple que el de D=5 sugra (que hay que ver que N coger) y tambien bastante interesante.
Mi pregunta se refiere a que un espinor de Dirac no es una representacion irreducible de Spin(1,3) y por tanto (segun tenia entendido) no puede representar una particula fundamental. Solo los espinores de Weyl o Majorana (en 4 dimensiones) pueden.
En cuanto a lo de Sugra, lo mas sencillo es coger la que menor supersimetria tiene en 5 dimensiones, N=2.
Puede que sea una cuestion de nomenclatura y me este haciendo viejo, nosotros hace veinte años todavia llamabamos a una particula fundamental a partir de aquello de Wigner de las representaciones unitarias del grupo de Poincare, y creo que lo primero que se hacia era separar los dos casos de masa igual o distinta de cero. Cierto que no teniamos ningun complejo en escribir (0,1/2) + (1/2,0), pero reservavamos la denominacion «Weyl» para el caso limite de masa cero.
Dicho mas contundentemene, si m>0 no habia fermiones de Weyl, son solo un formato comodo para las matrices gamma. Claro, eso lleva a que tienes que pegarte un buen rato discutiendo por qué no puedes meter masa ad-hoc a los fermiones en el langragiano de la interaccion electrodebil. En cambio, si partes axiomaticamente de que el bi-spinor no es fundamental, entonces exiges poner particulas con masa cero, te ahorras un monton de discusion, y puedes ir directamenta a lo de acoplar yukawas.
Yo criticaría un punto, al menos:
-Sólo una partícula el qubit.
Eso es si trabajas con un sistema cuántico de dos estados $latex vert 0rangle, vert 1rangle$, donde la partícula es el qubit, como un fermión con espín 1/2 o -1/2, o un fotón con dos polarizaciones.
Se puede tener un sistema cuántico con 3 «niveles». O también con d-niveles. N qubits son equivalentes a $latex 2^N$ estados de 2-niveles o bits clásicos, N-qudits (1 dit es un sistema cuántico con d «niveles»), son equivalentes a $latex d^N$ dits clásicos o estados con d-niveles.
Pregunta: ¿Qué es un sistema cuántico con $latex inf$ niveles? 😉 Supongo que hoy ando en una superposición cuántica coherente de todos mis posibles estados…
También diría que no hay ninguna cosa que haga a priori imposible trabajar en dimensión diferente a 3+1.
Bueno, no pretendía que fueras tú quién respondiera, sino iba para otros lectores. Obviamente, yo también sabía la respuesta. Debía haber avisado (abstenerse expertos o así o haber puesto ejercicio para friquis avezados) :(. La próxima vez, lo formularé de otra forma. De todas formas, gracias por responder :D.
LO que no sabía era lo de los fotones (no soy del campo de información cuántica e implementación experimental, aunque leo sobre el tema de vez en cuando). Ya que estamos, ¿tú crees en lo de D-wave? Yo me pregunto qué llegará antes, si la nueva física o el ordenador cuántico, en días como hoy.
«nosotros hace veinte años todavia llamabamos a una particula fundamental a partir de aquello de Wigner de las representaciones unitarias del grupo de Poincare»
Representaciones irreducibles (del grupo de Lorentz; en realidad, del grupo de Spin), y un espinor de Dirac no es una representacion irreducible. Me estoy perdiendo algo.
¿La masa? Aquellas representaciones, las de la clasificacion de Wigner, se etiquetaban por masa y spin. Las que tu dices se etiquetan solo con spin, ¿no?
Kac, a mí siempre me ha parecido cuando menos curioso, que pese a que los fermiones del modelo estándar son «Dirac», nadie ve «problemas», por dicho teorema de Wigner, en que sean «fundamentales» los espinores de Dirac.
No obstante, en términos semánticos lo son justo en la misma forma en que los «átomos» son las «unidades fundamentales» para hacer «química» y los tabulamos con la tabla periódica. Que los espinores de «Dirac» sean fundamentales a cierta escala de energía puede ser exactamente la misma cosas que el que los átomos sean «fundamentales» o no como sistemas a partir de cierta energía. Hablo en términos físicos en mis dos últimas frases.
NO tenemos una «tabla periódica» de las partículas elementales del modelo estándar. Lo más parecido que hay es, para los elementos de un álgebra de Clifford, es el teorema de periodicidad.
Acotación: según el teorema de Wigner (que yo sepa) son las representaciones unitarias irreducibles del grupo de Poincaré (o afinando más, del subgrupo de Poincaré, el grupo Lorentz, ¿no?) para ser más precisos (en el sentido del teorema de Wigner) las asociadas a la definición de «partícula».
O lo mejor también so me pierdo con esto, pero yo pensaba que eran del grupo de Poincaré en general (también está involucrado el grupo pequeño, «little group», pero no creo que Alejandro pensara en meterse hasta el fondo en la terminología exacta, creo que «nos entedemos»). Las partículas elementales las clasificamos según el teorema de Wigner con los autovalores de los operadores de Casimir. Para el grupo de Poincaré (ni no recuerdo mal) son la masa (raiz cuadrada del cuadrimomento o del momento en D dimensiones) y el (pseudo)vector de Pauli-Lubanski. El resultado es:
-Partículas massless (sin masa): números cuánticos masa y helicidad (relacionada con una cantidad del «vector» de Pauli-Lubanski y el cuadrimomento, al final, con el espín).
-Partículas masivas (con masa): números cuánticos masa y proyección del espín en la dirección del movimiento.
El teorema de Wigner ciertamente ha resultado muy productivo, a parte de avisarnos de algunos casos raros. Los que a mí siempre me han fascinado son los 3 siguientes:
1) La representación taquiónica (que generalmente rechazamos como no física).
2) La representación de espín continuo (es la más misteriosa en 4 dimensiones, creo que hace poco algunas personas han intentado hacer una teoría cuántica de campos para las «partículas» de espín continuo con idea de postularlas como candidata a materia oscura.).
3) En D=2+1 dimensiones, los aniones, o partículas con espín «arbitrario» ciertamente juegan un papel privilegiado en materia condensada y en otros sistemas físicos (no sé cómo anda el tema de la computación cuántica con aniones a nivel teórico y/o empírico mucho menos).
Francis: ¿recuerdas cuando pusiste aquella representación pictórica de las partículas del SM? ¿Cómo encajaría un anión o una partícula de espín continuo en aquella imagen? Del taquión mejor no hablo, son nuestros enemigos número uno…
La cuestion, entiendo, es si hay algun argumento basado en teoria de representaciones que te obligue a tener paridad cuando m>0 y por tanto a considerar «elemental» el bispinor (1/2,0)+(0,1/2).
Otra excusa podria ser que aquello de Wigner era definir particulas con representaciones unitarias del grupo de Poincare, y que definir particula simplemente como representacion general, no unitaria, no vale; que no hay representaciones unitarias de dimension finita del grupo de Lorentz y que lo que hacemos con las matrices gamma es una representacion antiunitaria. Pero eso solo anula toda la discusion y no entra al trapo.
Igual el truco esta en ver que lo que queremos meter en el langrangiano son terminos invariantes lorentz, esto es escalares, vectores, tensores, etc. Pero realmente igual podemos meter un termino sólo con particulas de Weyl a base de restar el vector y el axial_vector.
Sin embargo, lo que es notable es que la «clasificación» de Wigner de las partículas según las representaciones irreducibles unitarias del grupo de Poincaré ( no entraré a precisar más) las tabula con números, como la tabla periódica, PERO no tiene criterio de ordenación. La tabla periódica sí. Quiero decir, en la Tabla periódica de los elementos, según aumentamos Z, el número de protones del átomo, vamos rellenando períodos. No hay una tabla similar para la clasificación o más bien enumeración de Wigner. Ahí, hemos «perdido» algo. Aunque cierto es, que aún queda un poco de misterio en la tabla periódica, hay consenso en que la Mecánica Cuántica (y la Relatividad Especial) la explican. En este sentido, el teorema de Wigner es algo así como algo más primitivo a una tabla periódica más general, aunque ciertamente las generaciones del modelo estándar parecen indicar «cierta periodicidad» o «replicación», similar a la ley de las octavas, tenemos una ley de los «dobletes», y 3 generaciones. Las propiedades de las 3 generaciones son las mismas, salvo la masa y la «estabilidad».
Sandía. No me quería meter con los aniones, por eso sólo he mencionado sistemas cuánticos con cierto número de niveles. Un anión, una partícula de espín continuo, o también un quon, son objetos con los que definir un «estado» requiere un mayor cuidado… 🙂 Puedo estar equivocado, pero para especificar los estados de un anión hay que recurrir a una imagen con «cuasipartículas». Seguro Francis sabe algo más que yo de esto. A mí me interesa el tema de los aislantes topológicos cada vez más (por cierta analogía con el comportamiento de la gravedad en los horizontes de los BH: los grados de libertad gravitacionales parecen vivir en la superficie, justo como de forma análoga a como se comporta un aislante topológico -«conducen» sólo la corriente en su superficie no «in the bulk»).