Los libros de la serie DeMYSTiFieD de McGraw-Hill están bastante bien y el de teoría de cuerdas no es una excepción. Un libro para estudiantes de física e ingeniería que acerca la teoría de cuerdas a quien no ha cursado estudios en teoría cuántica de campos, pero conoce los fundamentos de la física relativista y de la física cuántica. Por tanto, muy recomendable para iniciarse. Su gran inconveniente es que la brevedad del libro obliga al autor a omitir la justificación física de muchos conceptos que se presentan. En mi opinión, David McMahon, «String Theory Demystified,» McGraw-Hill (2009) [320 pp.] no defraudará a quien no tenga miedo de las matemáticas de la teoría de cuerdas (simplificadas hasta el extremo, por supuesto).
No sé si un alumno de bachillerato podrá seguirlo sin problemas, pero sin lugar a dudas el esfuerzo merecerá la pena. Otros libros de McMahon como Relativity Demystified, Quantum Mechanics Demystified, y Quantum Field Theory Demystified son complementos ideales de este libro (yo también incluiría Supersymmetry Demystified de Patrick LaBelle). Un libro para estudiantes vocacionales que le acercará a los libros escritos por expertos, que suelen ser más avanzados.
Capítulo 1, «Introduction,» presenta toda la teoría general de la relatividad en dos páginas, toda la mecánica cuántica en cuatro páginas, y empieza a hablar de teoría de cuerdas en la página 10. Un inicio fuerte. Me gusta cómo se ilustra el origen de los infinitos en teoría cuántica de campos y la no renormalizabilidad de la gravedad (cuántica) de Einstein. Se justifica por qué la teoría de cuerdas introduce una distancia mínima (relacionada con la tensión de la cuerda) y se presentan de forma breve las cinco teorías de cuerdas, la teoría M, las D-branas y la idea de la compactificación. Más imposible.
Lo más importante del primer capítulo es entender que la teoría de cuerdas modifica la relación de indeterminación de Heisenberg, ΔxΔp~ℏ introduciendo la tensión de la cuerda (α’) de la forma Δx~ℏ/Δp + α’ Δp/ℏ. Ello implica una distancia mínima Δx~2 √α’. Por cierto, todos los capítulos tienen un cuestionario de autoevaluación (quiz), cuya solución está al final del libro.

«The Classical String I: Equations of Motion,» cap. 2 (pp. 21-50), introduce la acción que describe la partícula (puntual) relativista libre (no sujeta a fuerzas externas) en un espaciotiempo plano (Minkowski). Su trayectoria minimiza la longitud de su línea del mundo espaciotemporal. Se presentan ejemplos que son ejercicios (sencillos) resueltos en detalle. Se presenta la acción que describe una cuerda (bosónica) relativista libre en un espaciotiempo plano. Su trayectoria minimiza el área de su hoja del mundo (worldsheet) espaciotemporal. Se introduce el concepto de métrica inducida (la del espaciotiempo subyacente en el que se mueve la cuerda). El resultado es la acción de Nambu-Goto, ec. (2.19). Se deriva la ecuación del movimiento de la cuerda (una ecuación de onda lineal para su momento) y se describen sus posibles condiciones de contorno (Neumann, Dirichlet y periódicas).
Se presenta la acción de Polyakov (o modelo sigma) sin más detalles. Se recuerda el concepto de característica de Euler (χ) y se presenta para la esfera (2), el cilindro (0), el toro (0), la banda de Möbius (0) y la botella de Klein (0). Se presenta la acción de Polyakov para una hoja del mundo (σ, τ) con χ=0. Ello nos lleva a usar coordenadas en el cono de luz (τ+σ y τ−σ) y a obtener el desarrollo de Fourier de la solución general de la ecuación de onda, con modos a la izquierda XL(τ+σ) y a la derecha XR(τ−σ). Aplicando condiciones de contorno de Neumann se obtienen las cuerdas abiertas con extremos libres. Aplicando condiciones de contorno periódicas se obtienen las cuerdas cerradas; cuando se compactifica una dimensión en un círculo aparece el número de vueltas (winding) de la cuerda en dicha dimensión. Y usando condiciones de contorno de Dirichlet se obtienen cuerdas con extremos ligados a D-branas, con una longitud proporcional al número de vueltas.
El capítulo segundo debería ser comprensible para cualquier estudiante de física o ingeniería. Una buena manera de comprobarlo es realizar los ejercicios, que deben resultar fáciles. Quien encuentre dificultades en seguir los cálculos debería pensar en estudiar algún libro de mecánica clásica y/o de teoría clásica de campos. Lo mismo pasa con el capítulo tercero, «The Classical String II:
Symmetries and Worldsheet Currents,» que introduce un concepto clave, el tensor de energía-momento para la acción de Polyakov (en un ejercicio se debe demostrar que es equivalente a la de Nambu-Goto). Tras recordar la aplicación del teorema de Noether al campo electromagnético para obtener la conservación de la carga eléctrica, se muestra que la acción de Polyakov es invariante Poincaré, invariante ante reparametrizaciones en la hoja del mundo e invariante conforme (o Weyl). Estas dos últimas simetrías permiten reescribir la acción de Polyakov para una hoja del mundo plano (elección de un gauge) y calcular su tensor de energía-momento (1+1), que se anula. Falta discutir que esto implica que las vibraciones de la cuerda son transversales. También se presenta la conservación del tensor de energía-momento en el espaciotiempo subyacente.
Llegado a este punto ya se puede cuantizar la cuerda libre (primera cuantización) y presentar el álgebra de Virasoro. «String Quantization,» cap. 4, introduce la cuantización covariante (o canónica) y la cuantización en el cono de luz. Cualquiera que haya estudiado algo de mecánica cuántica debería entender la cuantización canónica usando la acción de Polyakov. Se introducen conmutadores espaciotemporales a tiempo fijo en la hoja del mundo de la cuerda y se obtienen las relaciones de conmutación para los modos (de vibración) transversales de la cuerda. Introduciendo operadores de creación/aniquilación de partículas (modos de vibración) aparecen estados de norma negativa (probabilidades negativas). Para eliminarlos se introducen los operadores de Virasoro en orden normal. Quien nunca haya oído hablar de estas técnicas deberá estudiar un libro de teoría cuántica de campos para entender su justificación, ya que McMahon no se molesta en comentar nada. Como una locomotora va a su ritmo sin mirar a su costado.
El cálculo del espectro de vibraciones para una cuerda abierta nos lleva a la famosa suma D/2 (1+2+3+4+···). Su aparición no tensa a McMahon, que aplica una técnica de regularización basada en multiplicar cada término por una exponencial negativa (mucha gente, como Lubos Motl, afirman que este es el método más sencillo para regularizar, pues evita hablar de la función zeta, variable compleja, etc.). El resultado es bien conocido D/2 (1+2+3+4+···) = −D/24. Usando las relaciones de conmutación para los operadores de Virasoro aparece la necesidad de tomar D=26 para eliminar los estados de la cuerda de norma negativa (que no son físicos). Como resultado los estados tienen una masa M² = (N−(D−2)/24)/α’. Para D=26 el estado fundamental tiene masa al cuadrado negativa, M² = −1/α’, es decir, es un taquión. En la página 81 del libro aparece el famoso taquión de las cuerdas bosónicas cuya eliminación requiere introducir la supersimetría. El primer estado excitado tiene M² = 0 para D=26, representando partículas sin masa (como el fotón y el gravitón).
El espectro de la cuerda cerrada es un poco más complicado, pues hay dos tipos de vibraciones transversales, las que se propagan hacia la izquierda y hacia la derecha. Duplicar fórmulas es fácil y el espectro resultante es similar. Aparece un taquión con M² = −4/α’, y los primeros estados excitados tienen M² = 0. Estos estados están descritos por un tensor cuya traza describe una partícula escalar sin masa, el dilatón. El tensor se puede descomponer en una parte simétrica y otra antisimétrica. La simétrica corresponde a una partícula de espín 2 (el gravitón), que cumple las ecuaciones de Einstein linearizadas. McMahon no da más detalles sobre la parte antisimétrica.
Los mismos resultados de pueden obtener usando cuantización en el cono de luz. Esta técnica evita los estados de norma negativa, pero a costa de perder la simetría Lorentz. Se discute brevemente (3 páginas) y se muestra que recuperar la simetría Lorentz requiere D=26. Lo que nos lleva al capítulo 5, «Conformal Field Theory Part I» (pp. 89-114), donde se nos dice que la teoría conforme de campos es una herramienta clave en el análisis perturbativo de las interacciones en teoría de cuerdas. Se comenta que las teorías de campos conformes en dos dimensiones tienen infinitas cargas conservadas, pero no tienen ninguna escala de masa o longitud asociada. La introducción de las coordenadas complejas, de la diferencia entre funciones holomorfas y antiholomorfas, y del grupo de transformaciones conformes en dos dimensiones es bastante elemental (aunque conocimientos previos de variable compleja se agradecerán).
Un punto clave es que los generadores de las transformaciones conformes Lm satisfacen el álgebra de Virasoro (con carga central nula, también llamada álgebra de Witten); recuerda, [Lm,Ln]=(m−n)Lm+n. La extensión central del álgebra de Virasoro con una carga central, es decir, [Lm,Ln]=(m−n)Lm+n+A(m)δm+n,0, donde A(m)=(c/12)m(m2−1) se deriva en el siguiente capítulo, «BRST Quantization» (pp. 115-126). En el cap. 6 se presenta el tercer método en el libro para cuantizar las cuerdas, el uso de operadores BRST para proyectar los estados físicos y descartar los no físicos (ghosts). La presentación es más matemática que física y lleva directamente a que la eliminación de la anomalía en el álgebra de Virasoro, A(m)=0, requiere un espaciotiempo con D=26 (25+1). Quien no haya leído estas cosas con anterioridad necesitará un libro de texto que discuta mejor los detalles.
El capíulo 7, «RNS Superstrings» (pp. 127-151) introduce la supersimetría mediante la acción de Ramon-Neveu-Schwarz (RNS) para las supercuerdas. Quien haya leído sobre mecánica cuántica relativista y la ecuación de Dirac no tendrá problemas en seguir el texto. Se introducen los espinores de Majorana, las transformaciones supersimétricas de la hoja del mundo de la cuerda (un superespacio en dos dimensiones) y la conservación del tensor de energía-momento. Las condiciones de contorno nos permiten distinguir entre cuerdas abiertas (tipo Ramond o tipo Neveu-Schwarz) y cuerdas cerradas (condiciones de contorno periódicas o antiperiódicas). El álgebra de Virasoro para las supercuerdas se llama álgebra super-Virasoro en el libro (aunque quizás sería mejor llamarla superálgebra de Virasoro), que difiere un poco entre supercuerdas abiertas R y NS. El espectro de las supercuerdas abiertas contiene un taquión (con masa m2=−1/(2 α’), donde α’ es la tensión de la supercuerda). La proyección GSO, que elimina los taquiones, y la dimensión crítica de las supercuerdas, D=10, se presenta de forma breve sin detalles.
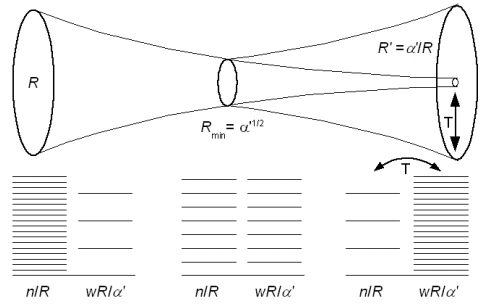
«Compactification and T-Duality» (cap. 8) introduce la compactificación de las dimensiones extra de las cuerdas bosónicas. Se compactifica en un círculo de radio R la dimensión X25, lo que permite introducir el número de vueltas (winding number), w=nR/α’, que se comporta como un momento lineal de una excitación de Kaluza-Klein. El espectro de partículas (vibraciones de las cuerdas) se extienden con partículas de Kaluza-Klein (con momento lineal p25=K/R). Estas partículas tienen quiralidad, pudiéndose descomponer p25=p25L+p25R, donde p25L=K/R+nR/α’, y p25R=K/R−nR/α’, es decir que nR=(p25L−p25R)/2. Estas ideas permiten introducir la dualidad T, que relaciona las teorías de supercuerdas tipo IIA y tipo IIB mediante R’↔α’/R, y n↔K. Los estados con (K,n) en una teoría con radio R se transforman en estados (n,K) en otra con radio R’=α’/R; estos estados (partículas) tienen la misma masa y el mismo álgebra de operadores de creación y aniquilación. Luego ambas teorías predicen la misma física.
Para cuerdas abiertas, que no tienen número de vueltas (w=n=0), la dualidad T transforma condiciones de contorno de Neumann (derivada nula en los extremos de la cuerda vibrante) en condiciones de Dirichlet (posición fija para los extremos de la cuerda). Las condiciones de Dirichlet están asociadas a los D-branas, a las que están fijadas los extremos de las cuerdas. Se presentan las D0-branas, D1-branas, …, hasta D24-branas. Compactificando n dimensiones los extremos de las cuerda son libres para moverse en las restantes 25−n dimensiones espaciales, que definen una D(25−n)-brana. La existencia de las D-branas en teoría de cuerdas es debida a la dualidad T, según el autor.
«Superstring Theory Continued» (pp. 167-186) introduce el superespacio y los supercampos (la supersimetría local en el espaciotiempo). Además de las coordenadas convencionales (bosónicas) xμ se introducen coordenadas de Grassman (fermiónicas) θA. En la hoja del mundo las coordenadas σs=(τ,σ) se extienden de igual forma, dando lugar a supercampos Y(σ,θ) sobre los que actúan los generadores de las transformaciones supersimétricas y, por tanto, tienen asociados supercargas. Para quien no haya visto con anterioridad la idea de la supersimetría el libro presenta de forma breve el cálculo (derivación e integración) con variables de Grassman.
La acción de Green-Schwarz considera que las supercuerdas se mueven en un superespacio, con coordenadas bosónicas Xμ(τ,σ) y fermiónicas Θa(τ,σ), donde las N supersimetrías dan lugar a N coordenadas fermiónicas (a=1,2,…,N). En teoría de supercuerdas N≤2 (cuerdas bosónicas con N=0, supercuerdas tipo I con N=1 y supercuerdas tipo IIA y tipo IIB con N=2). Se menciona la simetría kappa local y que restringe el número de dimensiones del espaciotiempo, pero no se dan detalles técnicos. En general el capítulo sobrevuela muchos temas omitiendo muchos detalles importantes. El lector que quiera entender este capítulo mejor tendrá que recurrir a otros libros de texto.
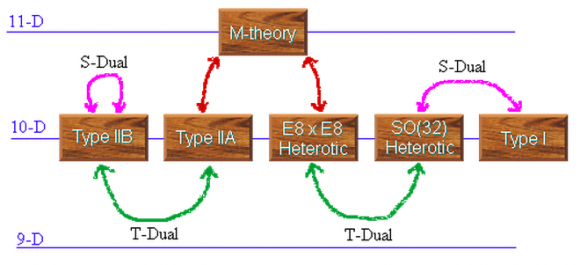
Los cinco tipos de teorías de supercuerdas se introducen en el capítulo 10, «A Summary of Superstring Theory» (pp. 187-194). La discusión es muy breve y se reduce a varias tablas; por ejemplo, se dedica media página a las teorías heteróticas HE y HO. Se menciona que la dualidad T relaciona las teorías IIA y IIB, y las heteróticas HE y HO, y que la dualidad S relaciona la teoría I con la HO, y que la IIB es S-autodual. Sólo se mencionan estas dualidades, sin más detalles técnicos.
Las teorías de supercuerdas tipo IIA y IIB se presentan (usando el formalismo GSO) en el cap. 11, «Type II String Theories» (pp. 206). Las teorías de supercuerdas heteróticas tipo HO y HE se presentan en el cap. 12, «Heterotic String Theory» (pp. 207-220). En ambos capítulos hay mucha teoría de grupos que se omite y casi todo se limita a discutir el espectro de partículas de estas teorías. Quien necesite conocer los detalles debe recurrir a libros de texto más avanzados.
Para hablar de agujeros negros y cosmología en teoría de cuerdas hay que introducir las D-branas. El capítulo 13, «D-Branes» (pp. 221-237) como hiperplanos en los que se mueven los extremos de las cuerdas abiertas. Tras dar la idea de nuestro universo como una D3-brana, del espaciotiempo inducido para las cuerdas bosónicas como una D25-brana y del superespacio inducido para las supercuerdas como una D9-brana, se introduce la cuantización de las Dp-branas siguiendo las ideas presentadas en el capítulo 4 (cuantización canónica de las cuerdas bosónicas). Tras ilustrar el espectro se indica que los estados de las cuerdas en presencia de D-branas se comportan como teorías gauge (presentan bosones vectoriales tipo gauge y bosones escalares asociados a roturas de simetrías).
En las teorías de supercuerdas tipo IIA sólo puede haber Dp-branas con p par, es decir, p=0,2,4,6,8 (recuerda que la dimensión del superespacio es D=10). Para las supercuerdas tipo IIB sólo hay Dp-branas con p impar, es decir, p=−1,1,3,5,7,9 (para p=−1 se obtiene un instantón). No se destaca que las D-branas son solitones de las teorías de supercuerdas. Se presentan los apilamientos de Dp-branas y los índices de Chan–Paton asociados a las cuerdas que tienen extremos en Dp-branas diferentes. Cuando coinciden N Dp-branas aparece una teoría de Yang-Mills con grupo U(N). Se ilustra en el caso U(2), es decir, dos Dp-branas coincidentes. Su espectro incluye 4 taquiones, 4 bosones vectoriales sin masa y 4 conjuntos de d−p bosones escalares sin masa. No se detalla como el grupo U(N) se transforma en SU(N) con un grupo U(1) resitual. Se remite al libro de Zweibach para los detalles (habrá reseña de este libro en próximas semanas).
El capítulo 14, «Black Holes» (pp. 239-254), tras introducir los agujeros negros de Schwarzchild y Kerr en relatividad general en D dimensiones, los agujeros negros extremales y la termodinámica de Bekenstein-Hawking, discute el cálculo de la entropía usando teoría de cuerdas para un agujero negro formado por una D1-brana con carga Q1 y una D5-brana con carga Q5. El cálculo sigue las ideas de P. R. Silva en arXiv:gr-qc/0605051 y conduce a que la entropía S=2π√(Q1Q5n)=A/(4Gs).
«The Holographic Principle and AdS/CFT Correspondence» (cap. 15, pp. 255-263) introduce de forma muy breve la idea del principio holográfico y la conjetura de Maldacena. «String Theory and Cosmology» (cap. 16, pp. 265-278) introduce la inflación cósmica, el modelo de Randall-Sundrum, los mundos brana y el universo ecpirótico (el big bang es producto de la colisión de mundos brana). Todo muy descriptivo, con pocos detalles matemáticos. Acaba el libro con un examen final y la respuesta (sin detalles) a los problemas/preguntas que acompañan todos los capítulos.
En resumen, un libro recomendable para los aficionados a la divulgación de la física que gustan de las fórmulas que tiene el gran mérito de repasar en sólo 306 páginas toda la teoría de cuerdas. En mi opinión faltan justificaciones físicas y matemáticas de todo lo que se presenta. El autor va a piñón fijo y no puede perder en explicar por qué está presentando lo que presenta. Por ello este libro dejará con cierto mal sabor de boca a quien busca algo más que fórmulas matemáticas. Muchas ideas importantes aparecen entre líneas y sólo tras haber estudiado otros libros de texto el lector que relea este libro se dará cuenta. Aún así, te recomiendo encarecidamente este libro si nunca te has enfrentado a las matemáticas de la teoría de cuerdas.






¡Gran reseña Francis 🙂 !
Este fue el libro donde aprendí por primera vez cuerdas 😀
Puedo contar mi experiencia:
En lo personal creo el libro es bastante bueno y accesible, estoy muy de acuerdo con la reseña, aunque yo recuerdo que cuando introduce la teoría cuántica de campos conforme me pareció muy oscuro y me costaba completar los detalles. También cuando se discuten agujeros negros me pareció mucho mejor la referencia que cita el autor que leer el propio libro.
Pero salvo ello en general el libro se agradece mucho para los que somos novatos, se hacen muchos detalles (como hacer explícita la cuantización de la cuerda bosónica) con cuidado y a un ritmo más rápido que Zwieebach, detalles que para otros (el libro de las Bécker) se mencionan de pasada.
En el curso de cuerdas que tomé me siguió pareciendo difícil estudiar la CFT, me ha costado mucho trabajo (y me cuesta), se agradecería mucho una referencia sencilla al tema. Me han comentado que el libro y las notas de Elias Kiritsis son amigables con este tema (Polchinski me pareció difícil, las bécker no explican casi nada y hay un libro enorme de CFT de Francessco que tarda muchísimo en ponerse interesante)