El libro de texto de teoría de cuerdas más recomendado a los estudiantes del grado de Física es el estupendo libro de Barton Zwiebach (Lima, Perú, 1954), profesor del MIT (Massachusetts Institute of Technology). Experto en teoría de campos cuerdísticos (string field theory), que el libro no discute, presenta la teoría de cuerdas en un lenguaje moderno con el mínimo de prerrequisitos (conocimientos básicos de mecánica cuántica, relatividad y teoría cuántica de campos). El libro presenta algunos temas avanzados, que otros libros similares suelen omitir por falta de espacio (este libro tiene 673 pp.). Por ello Barton Zwiebach, «A First Course in String Theory» (Second Edition), Cambridge University Press, 2009 [web del autor] es un libro muy recomendable.
El libro está dividido en dos partes: «Basics» (caps. 1-14) y «Developments» (cap. 15-26). La primera parte es un curso sobre teoría de cuerdas bosónicas (con un capítulo final sobre supercuerdas). La segunda parte discute temas más avanzados como la correspondencia AdS/CFT y sus aplicaciones en QCD, el cálculo de la entropía de los agujeros negros y la dualidad T entre otros.
El capítulo 1 introduce la búsqueda de una teoría de unificación en física fundamental. El electromagnetismo de Maxwell, la relatividad de Einstein, la teoría electrodébil de Weinberg y Salam, y el modelo estándar son ejemplos de unificación más o menos exitosa. Las teoría de gran unificación (GUT) y la supergravedad (SUGRA) son ejemplos de teorías poco exitosas. La teoría de cuerdas promete incorporar sus ideas en una unificación que pretende ser definitiva. Pero aún no hay verificación experimental de esta teoría. Zwiebach comenta que el descubrimiento de una cuerda cósmica, o de la supersimetría, o de dimensiones extra del espaciotiempo en la escala electrodébil, serían verificaciones experimentales definitivas. No sé si todos los lectores estarán de acuerdo.
La teoría de la relatividad especial en un espaciotiempo con dimensiones extra se repasa en el capítulo 2, «Special relativity and extra dimensions,» que incluye temas tan importantes como las coordenadas en el cono de luz (x+ y x−), el momento y la energía en estas coordenadas (p+ and p−), la idea de compactificar dimensiones extra en círculos (se ilustra con el cilindro) y las soluciones singulares tipo orbifold (se ilustran con el cono, pero no se volverán a discutir hasta el capítulo 13). La mayoría de los lectores no deberían tener problemas con este capítulo. Realizar todos los once ejercicios del final del capítulo es imprescindible para asegurar que se domina este lenguaje.
En el capítulo 3, «Electromagnetism and gravitation in various dimensions» (pp. 45-72), se revisa la formulación relativista (invariante Lorentz) del electromagnetismo clásico de Maxwell (recuerda Fμν ≡ ∂μ Aν − ∂ν Aμ). Tras ella se presenta la teoría de la relatividad general y la idea de la teoría clásica de Kaluza-Klein, en la que se compactifica una quinta dimensión en un círculo y se recuperan la gravedad de Einstein y el electromagnetismo de Maxwell. Se comentan los límites actuales sobre la posibilidad de que existan dimensiones extra grandes (en una escala submicrométrica) y que nuestro universo sea una D3-brana. También se comenta que la escala de longitud para las cuerdas podría ser mucho mayor que la escala de Planck (∼ 10−33 cm), pongamos ∼ 10−18 cm, con lo que su física se podría estudiar en los grandes colisionadores de partículas. De hecho, en el LHC del CERN se buscan señales de la teoría de cuerdas (aún sin éxito).
La ecuación de onda lineal para las oscilaciones transversales de una cuerda (no relativista) clásica se introduce en el capítulo 4, «Nonrelativistic strings» (pp. 73-88). No se presenta la ecuación de onda no lineal, pero se describen su condición inicial y las condiciones de contorno periódicas (cuerda cerrada), de extremos libres (Neumann) y de extremos fijos (Dirichlet). La frecuencia de las oscilaciones transversales se relaciona con la tensión de la cuerda, que tiene como unidades energía dividida por longitud y que es constante para la cuerda clásica. Se presenta la formulación lagrangiana (o hamiltoniana) y se derivan las ecuaciones anteriores a partir de la acción de la cuerda clásica. Todo estudiante de física debería haber estudiado estos conceptos en un curso elemental de mecánica y ondas.
El capítulo 5, «The relativistic point particle» (pp. 89-99) repasa la dinámica de la partícula libre en teoría de la relatividad especial usando el formalismo lagrangiano (su trayectoria en el espaciotiempo es una extremo (mínimo) de la acción S = m c ∫ ds). Este es el punto de inicio de la mayoría de los libros más avanzados (algunos lectores habrán agradecido los capítulos anteriores y otros los habrán considerado prescindibles). Se destaca la invarianza de la línea del mundo (world-line) ante reparametrizaciones del tiempo propio (τ). Se finaliza el capítulo introduciendo la fuerza de Lorentz (la ejercida por un campo electromagnético en una partícula cargada) en el marco del formalismo lagrangiano. Los ejercicios al final del capítulo son necesarios para profundizar en este último punto.
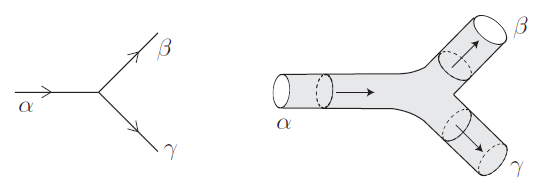
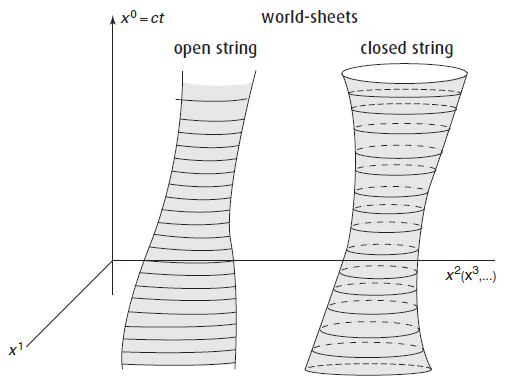
En un libro de teoría de cuerdas todo el mundo espera encontrar cuanto antes las cuerdas relativistas. Zwiebach las retrasa hasta el capítulo 6, «Relativistic strings» (pp. 100- 129). Quizás el capítulo más novedoso hasta el momento para el lector que nunca haya leído nada sobre teoría de cuerdas. Tras 11 páginas de justificación (usando pompas de jabón) se introduce la acción de Nambu–Goto (mejor llamada Nambu–Hara–Goto). Las ecuaciones de movimiento de la cuerda relativista son un extremo (mínimo) del área espaciotemporal de la hoja del mundo (worldsheet) de la cuerda abierta (o del tubo del mundo (worldtube) para la cuerda cerrada). La invarianza ante reparametrizaciones se aprovecha para introducir los rudimentos de la geometría diferencial de superficies. Además de las ecuaciones del movimiento se estudian las condiciones de contorno, destacando las de Dirichlet en las que los extremos de las cuerdas abiertas están ligados a D-branas (o Dp-branas). Por ejemplo, la D2-brana es un espacio tridimensional es un plano, sea x3 = 0, que se extienden en las otras dos coordenadas (x1, x2); una cuerda ligada a esta D2-brana tiene las coordenadas X3 de sus dos extremos exactamente nulas. Tras esta breve incursión en las D-branas se discute el tensor energía-momento para la cuerda y sus proyecciones en una D-brana.
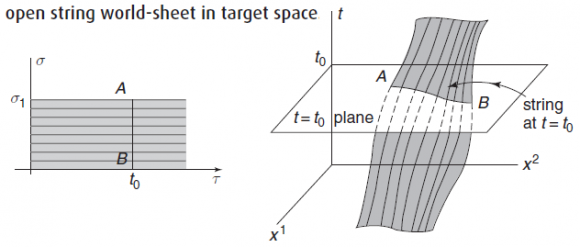
El capítulo 7, «String parameterization and classical motion» (pp. 130-153), refuerza el anterior discutiendo las ecuaciones de movimiento para cuerdas relativistas abiertas y cerradas. Para ello se recrea en la invarianza ante reparametrizaciones de la hoja del mundo, X(t,σ) ≡ X (t’,σ’); los detalles son excesivos, pero lo agradecerá quien no haya estudiado geometría diferencial. Se discute en detalle la fórmula de d’Alembert para la solución de la ecuación de onda de la cuerda, X(t,σ) = F(ct+σ) + G(ct−σ), así como el efecto de las condiciones de contorno (periódicas, Neumann y Dirichlet). Todo lujo de detalles para cuestiones que el lector debería conocer de un curso previo de mecánica y ondas. Finaliza el capítulo con una sección sobre cuerdas cósmicas, por su potencial relevancia experimental (según Zwiebach); el nivel es más alto que el resto del capítulo (menciona conceptos como geodésicas, cusps y ondas gravitacionales que exigen una discusión más extensa).
Los siete primeros capítulos constituyen un minicurso sobre teoría clásica de cuerdas relativistas. La cuantización de esta teoría se presenta en el capítulo 12, siendo los capítulos del 8 al 11 una introducción a los conceptos clásicos y cuánticos necesarios para entender dicho proceso en el formalismo del cono de luz. El capítulo 8, «World-sheet currents» (pp. 154-174), es de gran importancia (mucha mayor de la que sugiere el propio Zwiebach). Primero se revisa el teorema de Noether (no se menciona de forma explícita) en el contexto de la conservación de la carga eléctrica de una partícula cargada usando la formulación lagrangiana. Luego se aplica el teorema a la cuerda relativista, mostrando que la conservación del momento lineal implica la conservación de ciertas cargas (para cuerdas abiertas con condiciones de contorno de Dirichlet el momento no se conserva, pero se conserva el momento total cuando se incluyen el momento y las cargas de las D-branas en las que se encuentran los extremos de estas cuerdas). También se aplica el teorema a la invarianza de Lorentz de la cuerda conduciendo a la conservación del momento angular, la energía y el momento lineal. Se finaliza el capítulo con un breve descripción de las trayectorias de Regge y la conexión con los modelos duales (la teoría de cuerdas aplicada a la interacción fuerte entre hadrones); su valor histórico y Zwiebach lo presenta como de pasada.
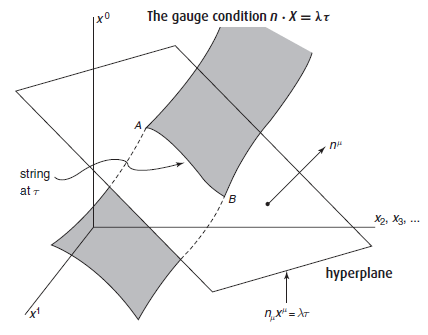
Las ecuaciones de la cuerdas relativistas tienen redundancias (invarianza ante reparametrizaciones) que impiden obtener una solución única salvo que se imponga una restricción adicional (gauge) a sus grados de libertad. El más sencillo es el gauge del cono de luz, que se presenta en el capítulo 9, «Light-cone relativistic strings» (pp. 175-193). La solución general en este caso para cuerdas abiertas y para cuerdas cerradas se puede desarrollar en serie de Fourier, lo que permite introducir los operadores de Virasoro. Conviene realizar todos los ejercicios al final del capítulo dada la importancia de este gauge en los siguientes capítulos.
Cuantizar las soluciones de la teoría de cuerdas en el gauge del cono de luz es sencillo, pero conviene entender cómo se cuantizan los estados para partículas escalares (como el Higgs), vectoriales (fotón) y tensoriales (gravitón). Los capítulos 10, «Light-cone fields and particles» (pp. 194-215), y 11, «The relativistic quantum point particle» (pp. 216-235), explican cómo realizar este proceso. Quien haya cursado teoría cuántica de campos entenderá fácilmente estos dos capítulos (aunque no todos los cursos presentan el formalismo del cono de luz); pero quienes no posean este prerrequisito necesitarán estudiarlos con atención y realizar todos los ejercicios, pues vale la pena el esfuerzo. Me hubiera gustado que Zwiebach dedicara más tiempo a la interpretación de los resultados en el contexto de la teoría cuántica de campos, que da pie a dicha interpretación en teoría de cuerdas (la llamada teoría de campos cuerdísticos).
La cuantización en el gauge del cono de luz se presenta en el capítulo 12, «Relativistic quantum open strings» (pp. 236-279), para cuerdas bosónicas abiertas, y en el capítulo 13, «Relativistic quantum closed strings» (pp. 280-306), cuerdas bosónicas cerradas. En ambos casos se obtiene la dimensión crítica para el espaciotiempo inducido (D=26) y la aparición de taquiones (estados de masa al cuadrado negativa). Los estados siguientes son de masa nula y corresponden a partículas vectoriales de espín 1 y D−2 componentes (cuerdas abiertas) y partículas tensoriales de espín 2 y (D−2)² componentes (cuerdas cerradas). Estos últimos representan el gravitón (parte simétrica del tensor), el campo tensorial antisimétrico de Kalb–Ramond y el campo escalar llamado dilatón. Se destaca que la constante de acoplo entre cuerdas no es constante sino que depende del campo dilatón. Lo más curioso son las secciones 12.8 sobre la interpretación de las D-branas como hechas (de estados condensados) de taquiones (Zwiebach no podía omitirlo), y 13.5 y 13.6 sobre singularidades (orbifolds) en cuerdas cerradas.
La primera parte se centra en las cuerdas bosónicas, pero incluye un capítulo final sobre supercuerdas (tema cuyo estudio requiere libros de texto más avanzados que el Zwiebach). El capítulo 14, «A look at relativistic superstrings» (pp. 307-327), introduce la supersimetría local (añadiendo operadores que anticomnutan en la hoja del mundo), incluyendo las supercuerdas abiertas de Ramond y de Neveu–Schwarz, así como las supercuerdas cerradas de tipo II. La discusión es breve y sólo se mencionan como de pasada las cinco teorías de supercuerdas en D=10, llamadas tipo I, tipo IIA, tipo IIB, heterótica E8 × E8, y heterótica SO(32), sin ni siquiera mencionar su grupo de recubrimiento Spin(32)/Z2.
Resumiendo, la parte I es un libro elemental sobre teoría de cuerdas bosónicas de 327 páginas que está bien escrito y puede satisfacer a la mayoría de los lectores/estudiantes. Queda en el aire el para qué sirve todo esto. La parte II presenta varias aplicaciones físicas de los resultados de la parte I. Se pueden leer sus capítulos en orden o ir saltando de uno a otro en función de los intereses personales. Pero resulta casi imprescindible leer (o estudiar) el capítulo 15, «D-branes and gauge fields» (pp. 331-355), sobre D-branas. Las cuerdas (bosónicas) con extremos libres (condiciones de contorno de Neumann) se mueven en una D25-brana, pero pueden tener sus extremos fijos (condiciones de contorno de Dirichlet) a una Dp-brana (1 ≤ p < 25), cuyo volumen del mundo (world-volume) es (p+1)-dimensional.
Las D-branas vibran de manera similar a las cuerdas, aunque son más rígidas, y sus vibraciones se pueden cuantizar de forma similar. El resultado es que toda Dp-brana tiene un campo vectorial (tipo U(1) como el electromagnetismo de Maxwell) que acarrea cargas eléctricas y magnéticas, así como tantos campos escalares como direcciones transversales que residen en su volumen del mundo. Varias branas pueden ocupar el mismo volumen (pueden estar superpuestas) de tal forma que las cuerdas tienen sus extremos en diferentes branas; en dicho caso estas branas apiladas tienen un campo vectorial de Yang–Mills (tipo U(n) para n D-branas apiladas) caracterizado por pares de índices de Chan–Paton. También puede haber cuerdas entre una Dp-brana paralela a una Dq-brana (asumiendo p > q).
Las cargas de las D-branas se pueden considerar cargas colocadas en los extremos de las cuerdas abiertas que las definen. Las cuerdas cerradas (y las cuerdas abiertas orientadas) también pueden tener cargas distribuidas a lo largo de su longitud gracias al campo (antisimétrico) de Kalb–Ramond, que acompaña al campo (simétrico) del gravitón y al campo (escalar) del dilatón. Nos lo cuenta Zwiebach en el capítulo 16, «String charge and electric charge» (pp. 356-375). Esta densidad de carga a lo largo de las cuerdas interacciona en sus extremos con la carga asociada a las D-branas. En la teoría bosónica las D-branas no pueden tener un campo de Kalb–Ramond en su volumen (que en este caso es un tensor antisimétrico de más de dos índices), pues las correspondientes D-branas son inestables. Sin embargo, las supercuerdas cerradas tipo IIA y tipo IIB pueden tener algunas Dp-branas estables con este tipo de densidad de carga. En las supercuerdas tipo IIA existen campos de Kalb–Ramond Aμ acoplado a las D0-branas y Aμνρ acoplado a las D2-branes; en las supercuerdas tipo IIB existen campos Aμν acoplado a las D1-branas y Aμνρσ acoplado a las D3-branas. Más aún, gracias al acoplo con el campo del taquión, las Dp-branas con p par (D4, D6, D8) son estables en la teoría tipo IIA e inestables en la IIB, pero las Dp-branas con p impar (D5, D7, D9) son estables en la teoría IIB e inestables en la IIA.
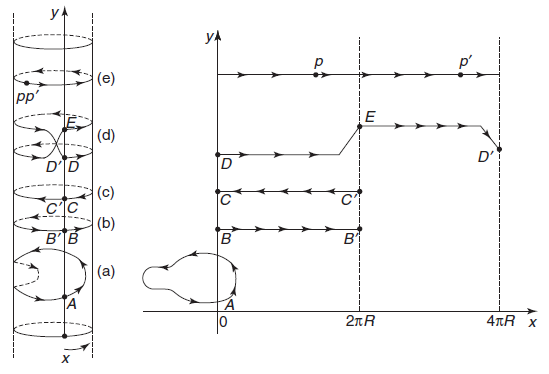
La dualidad T se discute en los capítulos 17, «T-duality of closed strings» (pp. 376-399), 18, «T-duality of open strings» (pp. 400-414), 19, «Electromagnetic fields on D-branes» (pp. 415-432), y 20, «Nonlinear and Born−Infeld electrodynamics» (pp. 433-450). La dualidad ya se observa en la física clásica, por ejemplo, en el electromagnetismo de Maxwell en ausencia de cargas se cumple que (E,B) → (−B,E). En la teoría de cuerdas la manera más sencilla de ilustrar la dualidad T es considerar cuerdas cerradas en un cilindro, obtenido al compactificar una dimensión en un círculo, como se ilustra tanto a nivel clásico como cuántico en el capítulo 17. Para cuerdas abiertas la dualidad T también afecta a las Dp-branas en las que se encuentran sus extremos, transformándolas en D(p−1)-branas (sólo para p ≥ 2), como ilustra el capítulo 18. Las cargas en las D-branas también se ven afectadas por la dualidad T como se muestra en el capítulo 19. Finalmente, el capítulo 20 presenta un tema avanzado, la electrodinámica no lineal de Born−Infeld, que garantiza que la autoenergía de las cargas puntuales es finita. Este tipo de campo surge de manera natural en las D-branas y muestra como los objetos fundamentales de la teoría de cuerdas regularizan la carga eléctrica del electrón.
La teoría de cuerdas es un paradigma que permite desarrollar modelos físicos. Entre ellos se incluyen todas las teorías que se usan en la actualidad en cualquier rama de la física, luego puede tener aplicaciones de toda índole. Pero la mayoría de los estudiantes piensa en su aplicación como teoría de todo que unifica el modelo estándar de las partículas y la gravedad de Einstein. Hay muchas maneras de obtener el modelo estándar en teoría de cuerdas, pero Zwiebach se decanta por usar intersecciones de D6-branas en una teoría de supercuerdas tipo IIA, como nos cuenta en el capítulo 21, «String theory and particle physics» (pp. 451-494). El gran problema de estos modelos es que no especifican los parámetros del modelo estándar (cuyo valor se debe obtener de los experimentos) y tampoco justifican su contenido (en cierto sentido la teoría de cuerdas puede modelar el contenido de partículas de cualquier universo posible, el llamado problema del paisaje (landscape) o problema del vacío).
Como todos los modelos fenomenológicos para el modelo estándar en el paradigma de la teoría de cuerdas el resultado parece ad hoc y no predice de forma general ningún fenómeno nuevo más allá del modelo estándar. Por supuesto, cualquier nuevo descubrimineto experimental se puede incorporar a estos modelos, como nuevos grupos gauge U(1)’, SU(2)’, SU(3)’ (o tecnicolor), nuevas generaciones de partículas (en teoría de cuerdas se prefieren números pares de generaciones), o incluso nuevas partículas exóticas (axiones, monopolos, etc.). Esta gran libertad es propia de todo paradigma y los críticos de la teoría de cuerdas la exponen como problema, cuando bien mirado es una gran virtud.
Zwiebach nos habla de la termodinámica de los agujeros negros en la teoría de cuerdas en el capítulo 22, «String thermodynamics and black holes» (pp. 495-524). Se discute la termodinámica de las cuerdas tanto para un conjunto de cuerdas abiertas cuyos extremos se encuentran en una D0-brana y para un conjunto de cuerdas cerradas. El cálculo de la función de partición indica que hay una temperatura máxima, la temperatura de Hagedorn, más allá de la cual se cree que se produce una transición de fase. Tras esta breve incursión en la termodinámica de las cuerdas se presenta la termodinámica de los agujeros negros. La teoría de cuerdas permite calcular la entropía de los agujeros negros que se forman al apilar muchas Dp-branas. Se presenta la cuenta del número de estados de cuerdas entre D1-branas con carga Q1 y D5-branas con carga Q5 para un agujero negro extremal (cargado con carga máxima). Por desgracia este tipo de modelos cuerdísticos no son aplicables a agujeros negros sin carga, como los de Schwarzschild.
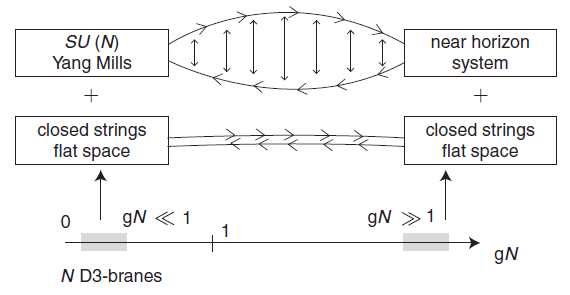
El capítulo 23, «Strong interactions and AdS/CFT» (pp. 525-567), presenta la aplicación del paradigma de la teoría de cuerdas a la interacción fuerte entre quarks (que en el modelo estándar describe la cromodinámica cuántica o QCD). Se recuerda la teoría de finales de los 1960 sobre las cuerdas en rotación de Susskind para explicar los mesones y las trayectorias de Regge. Se presenta el límite para gran número de colores en una teoría de Yang-Mills SU(N) siguiendo las ideas de ‘t Hooft. Todo ello sirve de motivación para la correspondencia AdS/CFT o gravedad/gauge de Maldacena. Se discute la formulación original de la conjetura del físico argentino con cierto detalle. Finalmente se esboza su aplicación al plasma de quarks y gluones. Este capítulo es uno de los más interesantes de la segunda parte del libro.
En los tres últimos capítulos del libro Zwiebach parece sentir cierto escozor por no haber tocado temas clásicos en todos los libros de texto de teoría de cuerdas, como la acción de Polyakov, la cuantización covariante o el cálculo de las interaciones entre cuerdas usando superficies de Riemann. El capítulo 24, «Covariant string quantization» (pp. 568-590), y el 25, «String interactions and Riemann surfaces» (pp. 591-629) discuten estas cuestiones. El más intersante es el capítulo 26, «Loop amplitudes in string theory» (pp. 630-658) que presenta argumentos a favor de la finitud de la formulación perturbativa de la teoría de cuerdas. No se presenta una demostración rigurosa pero los argumentos son firmes y convencen a cualquiera. Sin embargo, como el paradigma de la teoría de cuerdas va mucho más allá de la teoría perturbativa, estos argumentos requieren un análisis más avanzado para llegar a convencer a los más críticos.
En resumen, un gran libro de texto, de nivel elemental (sobre todo la primera parte), que disfrutarán los estudiantes del grado de Física que quieran saber más sobre el paradigma de la teoría de cuerdas.








Primero agradecerte tu reseña. La anterior sobre el libro de Mcgraw Hill «String Theory Demystified» Me ha llevado a comprarme también el de Relatividad General y el de Teoría Cuántica de Campos de la misma serie. Ambos me han encantado y me están haciendo más llevables las interminables noches de calor de este verano. Recomiendo esta colección de libros a todo el mundo. En cuanto termine de repasar – recordar la relatividad general y de estudiar-machacar la teoría cuántica de campos me he prometido empezar con las cuerdas.
Para ello tendré muy en cuenta tus reseñas y espero tener pronto a mi disposición tu libro sobre cuerdas.
Sobre cuerdas una pequeña cuestión hoy después de leer esta reseña he curioseando por la red y me he encontrado con la famosa suma de los naturales igual a -1/12 su relación con la función zeta de Riemann e incluso el efecto Casimir. De acuerdo yo no soy quién para cuestionar esto. ….pero
¿De verdad uno puede ir por la vida afirmando que los infinitos naturales suman -1/12? Así sin más. Parece que falta alguna hipótesis adicional algo que te prepare para semejante golpe.
A los ojos de un profano simplemente está diciendo que no tienes ni idea de lo más elemental sobre series. Gracias por tu atención.
Por supuesto uno no puede decir que la suma de todos los naturales es -1/12 sin dejar claro el contexto. Dicho de forma suelta está mal, pero si uno está familiarizado con estos temas entonces puede dejar un poco de lado las precisiones. La historia está en que el publico general no conoce el contexto donde esa afirmación es cierta así que de primeras puede parecer sorprendente.
Si me permites unos comentarios Alejandro:
Que bueno que te gustasen los libros de la serie Demystified. Debo advertirte que lo que a mi me disgustó el hecho de que poseyesen varias erratas, te recomiendo tengas mucho cuidado (en el cuerdas en particular si lo sigues con cuidado podrás darte cuenta). Pero fuera de ello la idea de poner al alcance de todos temas tan emocionantes es una idea fabulosa.
Por cierto el de relatividad tiene varios temas avanzados y explicados de manera fenomenal 🙂 ya verás que cuando arribes al formalismo de Newmann-Penrose os vas a divertir mucho. Un detalle señalable es que a lo mejor sería bueno que revisases el libro de Wheeler para que veas como se hacen los cálculos usando el formalismo tensorial. Pues en el libro de McMahon se discute casi enteramente todo usando formas diferenciales que son un formalismo bellísimo pero nunca deja de ser bueno usar el formalismo tensorial a veces.
Sobre el post:
El libro de Zwiebach 🙂 A mi me gustaron mucho los capítulos iniciales. Para mi fue una gran aventura estudiar la dinámica relativista de una cuerda. El asunto no es trivial como hacen creer muchos, por ejemplo en el libro de las Bécker (creo que tengo una frustración con este jejej) en la primeras 59 hojas ya se discutió todo lo que hace Zweiebach en medio libro y pienso que vale muchísimo la pena aprender lo que discute este último pues la física relativista de objetos extendidos es fantástica, digna de mostrarse y además (según yo) la dinámica no es nada trivial.
Alejandro:
El asunto de la regularización de la serie de los naturales no es trivial y a lo mejor soy lento pero a mi no me quedó claro cuando leí por primera vez la discusión de McMahon. Vale la pena que le pongas atención te adjunto unos enlaces de utilidad:
Anotaciones conceptuales:
http://motls.blogspot.mx/2007/09/zeta-function-regularization.html
Motivación matemática:
http://gaussianos.com/como-que-1248-1/
Esta es la discusión formal:
http://arxiv.org/pdf/hep-th/9510105v1.pdf
Por cierto te recomiendo que tengas un poco de cuidado en la discusión de CFT a mi me pareció oscura. Pero hay muy buenos otros libros con los que puedes complementar la lectura.
Saludos
Hola Alejandro, me gustaría preguntarte si no es mucha molestia, donde has leído sobre la relación entre la suma de los infinitos números naturales y el efecto Casimir.
Planck, la relación aparece en teoría de cuerdas. Recuerda que el efecto Casimir es debido a la energía del vacío. El propio Zwiebach lo comenta en su libro.
En toda teoría cuántica de campos la energía del vacío es infinita (hay infinitos osciladores armónicos, cada uno tiene una energía del vacío finita (-1/2) y se integra (suma) en un volumen infinito); sólo tienen sentido físico los estados con energía respecto a la energía del vacío, es decir, todos los estados físicos deben tener una diferencia de energía finita respecto al vacío. Por tanto, por convenio, se puede fijar la energía del vacío en un valor finito y hacer que los estados físicos tengan energía finita (en caso contrario tendría energía infinita, pero siempre tal que la diferencia respecto al vacío fuera finita, algo engorroso). ¿Qué valor elegir para el vacío? En teorías cuánticas de campos con un único vacío la respuesta es obvia (cero). Pero en las que tienen varios vacíos hay que elegir por convenio (el campo de Higgs tiene dos vacíos y se sabe que la diferencia entre ellos es 246 GeV; se asume que a alta energía el vacío tiene energía cero y que a baja energía el vacío tiene 246 GeV, pero podría ser al revés, el vacío a baja energía tener energía cero y el vacío a alta energía tener -246 GeV).
En teoría de cuerdas el valor del vacío del campo (inestable) de taquiones debe ser tal que ciertas anomalías se cancelen para las dimensiones críticas del espaciotiempo (D=10 en supercuerdas y D=26 en cuerdas). El valor 1+2+3+4+… = -1/12 es el mejor convenio posible (de hecho en matemáticas se considera el mejor valor posible para dicha suma). En teoría de cuerdas regularizar usando la función zeta simplifica los cálculos y tiene justificaciones más allá del cálculo del vacío (en la termodinámica de las cuerdas).
Saludos
Francis
Pues el jefe google todo lo sabe, te pongo dos enlaces:
Creo que lo he leído en este enlace que ahora falla, (hasta tenia un link a un pdf para el cálculo detallado del efecto casimir)
http://revolucioncientifica.com/matematicas%20y%20realidad/elsecretomejorguardadodelasmatematicaselinfinitovale.asp
De segundas también lo he encontrado aquí
https://es.answers.yahoo.com/question/index?qid=20150502104141AA9HGx8
Muy interesante el post de Terry Tao, «The Euler-Maclaurin formula, Bernoulli numbers, the zeta function, and real-variable analytic continuation,» What’s new, 10 Apr 2010.
Planck:
Yo lo leí en estas notas hace poco http://www.damtp.cam.ac.uk/user/tong/qft/qft.pdf
Página 27. Espero lo encuentres interesante
Gracias Francis por tu explicación detallada y a Ramiro por el enlace. Ya conocía esta relación, le preguntaba a Alejandro por la fuente porque me parecía que, por lo que decía, lo había leído en mi página web. El primer enlace que adjunta confirma mis sospechas. ¡Pensaba que nadie leía mis artículos! Además, lo preguntaba porque en mi artículo queda bastante claro (creo) que esta suma no corresponde a la suma usual que usamos de forma cotidiana e incluso planteo una forma de «desmitificar» o de tratar de explicar el resultado basándome en el artículo de Lubos: http://motls.blogspot.com.es/2014/01/sum-of-integers-and-oversold-common.html. Por esto me parecía raro que Alejandro preguntase como es posible que una suma usual de ese resultado… Perdón si todo esto ha podido sonar a autobombo.
PD: Francis, no te olvides de avisar cuando tengas tu libro sobre cuerdas preparado para publicar (tomate todo el tiempo que necesites). Seguro que muchos de tus seguidores (yo incluído por supuesto) están deseando leerlo.
¿Sabes lo que es un paradigma? Quizás deberías consultar un libro que te lo explique.
¡ Excelente resumen como siempre Francis ! Este es el libro que yo utilicé para tratar de entender algo sobre cuerdas. En mi opinión el libro es excelente y en principio accesible a cualquier persona con un mínimo de conocimientos de cuántica, relatividad y QFT.
Recuerdo que estaba ansioso por llegar al capítulo 21 donde se explica como generar el SM a partir de una intersección de D6 branas. Después de leerlo me quedé bastante perplejo, como dice Francis todo eran «predicciones» ad-hoc: para generar los quarks hacen falta 3 branas para el grupo SU(3) y los 3 colores de la fuerza fuerte que van a otras 2 branas que representan el grupo SU(2) de la fuerza débil. Otra nueva brana para los anti-quarks y para explicar la quiralidad del SM, otras 2 para los leptones… al final necesitamos un total de 9 D6 branas que deben ser coincidentes. Todo esto deja una sensación agridulce: por un lado las combinaciones de cuerdas entre branas dan el número correcto de partículas de cada clase y el número correcto para valores como la hipercarga, por otro parece claro de que de esta forma podemos «predecir» casi cualquier cosa…
Lo que más me impactó fue cuando explica que la ruptura espontánea de la simetría se produciría al separarse las branas coincidentes (aunque todavía nadie ha sido capaz de proponer un modelo realista de como exactamente se produce) y cuando explica como la intersección de 2 branas de 6 dimensiones en un espacio-tiempo de 10 hacen que estas se crucen 3 veces, lo que explicaría las 3 generaciones de quarks y leptones (aunque la magia desaparece un poco al destacar que esto se produce para una de las muchas probabilidades posibles).
Pese a esta sensación agridulce la lectura del libro es apasionante, los primeros capítulos te hacen ver que las cuerdas son la opción más natural para expandir la exitosa QFT, como las cuerdas producen las «world-sheet» al desplazarse por el espacio-tiempo, como sus modos de vibración coinciden con las partículas que vemos, como surge el gravitón de forma natural en la teoría… entender estos conceptos aunque sea de forma superficial produce una sensación indescriptible y una convicción de que la teoría tiene unas bases muy sólidas que deben de alguna forma describir el Universo que habitamos. El poder de las matemáticas es absolutamente increíble…
Francis como siempre un placer leer tu reseñas acerca de los libros que tratan sobre Teoría de Cuerdas, te felicito!
En lo referente a Barton Zweibach, deseo expresarte mi orgullo y admiración por tan distinguido investigador peruano, el cual desde 1984 viene divulgando a través de diversas entrevistas, artículos escritos, charlas y conferencias todo lo concerniente a las características y desarrollo de dicha teoría, por lo que vayan para él y su familia, un fuerte abrazo desde Perú¡
Parecía interesante hasta que he llegado a identidad de Euler,… después «divina proporción»,… «problema de los tres cuerpos»,… en fin,…
No falta el «hegeliano» de turno….
Me convenciste de compralo.