La teoría de cuerdas tiene dos tipos de objetos fundamentales, (super)cuerdas y (D-)branas. Las D-branas se comportan como solitones para las ecuaciones no lineales de la teoría de cuerdas. Por ello son imprescindibles para entender el presente y el futuro del paradigma de la teoría de cuerdas. El libro de Koji Hashimoto “D-Brane. Superstrings and new perspective of our world,» Springer (2012) [pp. 165], nos cuenta en un lenguaje sencillo las ideas básicas sobre la teoría de D-branas, eso sí, usando algunas fórmulas (porque está dirigido a estudiantes del grado de física). Por ello, los buenos aficionados a la divulgación disfrutarán de este librito muy recomendable (que creo asequible para los estudiantes de bachillerato más motivados).
Los lectores que nunca hayan oído hablar de solitones en teorías cuánticas de campos disfrutarán con el clásico R. Rajaraman, «Solitons and instantons: An introduction,» North-Holland (1989) [418 pp.]. Como libro más riguroso y moderno recomiendo N. Manton, P. Sutcliffe, «Topological Solitons,» Cambridge University Press (2004) [506 pp.]. Pero hay muchos más.
El libro de Hashimoto está dividido en ocho capítulos. El primero, «From Elementary Particles to D-Branes and Strings» (pp. 1-12), introduce y justifica los contenidos del resto. «Toda la materia y todas las interacciones del universo están hechas de D-branas,» más aún, «vivimos en una D-brana» (según la idea de los mundos brana). Las D-branas son los lugares donde las cuerdas abiertas tienen sus extremos, pero además son capaces de emitir cuerdas cerradas, tienen cargas eléctricas y/o magnéticas, y corresponden a solitones en la teoría de cuerdas (branas negras en una teoría de supergravedad).
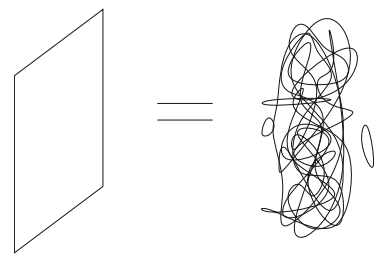
La mayoría de los libros sobre teoría cuántica de campos se centran en los estados tipo vacío y tipo partículas, pero en las teorías no lineales, como las de Yang-Mills, también existen estados no lineales, soluciones de tipo solitón. Las «D-branas son los solitones de la teoría de cuerdas» por ello el capítulo 2, «Solitons and Elementary Particle Physics» (pp. 13-48), introduce este concepto para quienes no lo conozcan. Obviamente, salvo en teorías de campos muy excepcionales, los «solitones» son ondas solitarias («paquetes de energía que se mueven como partículas»), a diferencia de las solitones en sentido estricto de las teorías de campo completamente integrables; más en concreto, son solitones topológicos que conectan diferentes estados de vacío (en teorías que tienen más de un estado de vacío). Hashimoto no discute en detalle la diferencia, que en mi opinión es muy importante, dado que las teorías cuerdas son teorías de campos conformes.
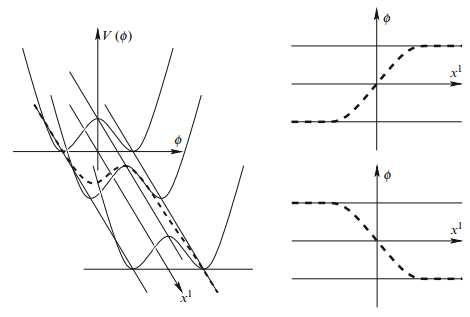
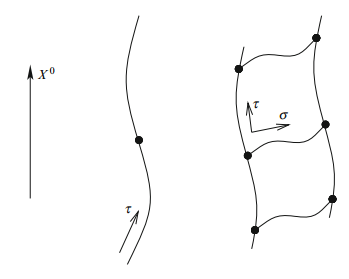
Tras discutir la necesidad de una teoría de todo que resuelva los problemas del modelo estándar de las partículas y la teoría cuántica de la gravedad, se presentan las ideas básicas sobre los solitones en teoría de campos. Un punto clave es que las soluciones en 1+1 dimensiones se pueden prolongar a soluciones en d+1 dimensiones introduciendo simetrías translacionales. Usando el ejemplo de la teoría de campos ϕ4 en 1+1 dimensiones se presentan las soluciones de tipo rizo y antirrizo (kink y antikink), que conectan dos estados de vacío. Su interpretación más sencilla es como un estado condensado de taquiones (las partículas en un estado de vacío inestable pueden evolucionar a partículas en otro estado de vacío estable, pero también pueden dar lugar a un estado condensado del campo con mayor energía de tipo solitón).
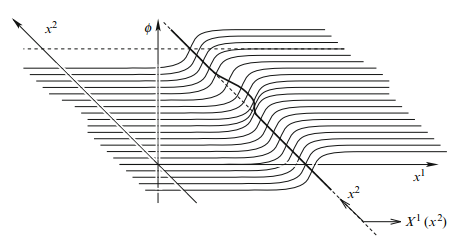
La construcción de soluciones de tipo solitón en múltiples dimensiones es más difícil. En 2+1 dimensiones estos solitones topológicos corresponden a los llamados vórtices y en 3+1 dimensiones a los monopolos magnéticos (propios de cualquier teoría de gran unificación, o GUT). La dualidad entre partículas (con carga tipo eléctrica) y solitones de tipo monopolo (con carga tipo magnética) se ilustra con la teoría de Dirac (1931) para los monopolos magnéticos en el electromagnetismo clásico de Maxwell. Y se comenta en el contexto de las teorías de Yang-Mills, aunque sin detalles matemáticos.
Las D-branas son solitones (topológicos) multidimensionales en la teoría de cuerdas, como se nos ilustra en el capítulo 3, «Dimensions of Solitons, Dimensions of String Theory» (pp. 49-66). Hashimoto nos presenta el leitmotiv «todos vivimos en un solitón» («people live on the soliton«). Los solitones en un espaciotiempo con 3+1 dimensiones tienen un volumen del mundo (wordvolume) con p+1 dimensiones y una codimensión 3–p. Por ejemplo, el rizo (kink) en un espaciotiempo de 3+1 dimensiones tiene codimensión 1 y un volumen del mundo con 2+1 dimensiones. El vórtice (vortex) en 3+1 dimensiones tiene codimensíon 2 y un volumen del mundo con 1+1 dimensiones. Y el monopolo en 3+1 dimensiones tiene codimensión 3 y un volumen del mundo con 0+1 dimensiones.
¿Qué pasa en un espacio tiempo con D dimensiones (D–1 espaciales y 1 temporal)? El solitón con volumen del mundo con p+1 dimensiones tiene codimensión D–p. Los monopolos tienen codimensión D, luego su línea del mundo (worldline) tiene 0+1 dimensiones (por eso un monopolo se comporta como una partícula). Los vórtices tienen codimensión 2 y su volumen del mundo es (D–2)+1 dimensional. Y los rizos (kinks) tienen codimensión 1 y un volumen del mundo con es (D–1)+1 dimensiones. En pie de igualdad las Dp-branas tienen codimensión (D–p), dimensión del bulk, y un volumen del mundo con p+1 dimensiones (p espaciales y 1 temporal).
Hashimoto nos introduce las cuerdas cósmicas, defectos lineales en el espaciotiempo surgidos durante la gran explosión (big bang), como vórtices en el espaciotiempo en 3+1 dimensiones. Los mundos branas (nuestro espaciotiempo macroscópico como una D3-brana cuyo volumen del mundo tiene 3+1 dimensiones) nos llevan a las cuerdas (bosónicas) y su espectro con un taquión cuya masa m cumple m2=−1/ls2, donde ls es la longitud de la cuerda, relacionada con su tensión α’ = 1/(2π ls2), y una serie de partículas con masa nula. Se finaliza con la idea de compactificación y la posibilidad de que las cuerdas sean D2-branas curvadas en forma de cilindro con radio decreciente.
El capítulo 4, «D-Branes» (pp. 67-81), nos introduce las D-branas y su conexión con los agujeros negros en una teoría de la supergravedad (branas negras); por cierto, los agujeros negros son soluciones de tipo solitón de las ecuaciones de Einstein de la gravedad (A. Salam, J. Strathdee, «Black holes as solitons,» Physics Letters B 61: 375-376, 1976, doi: 10.1016/0370-2693(76)90592-X). El espectro de partículas sin masa de las cuerdas (Hashimoto considera las supercuerdas en una teoría de tipo IIB) en 10 dimensiones contiene el campo de la gravedad (tensor simétrico gMN), el campo de Kalb–Ramond (tensor antisimétrico BMN), el dilatón (campo escalar ϕ) y los tres campos de Ramond–Ramond C, CMN, CMNPQ. Las (super)cuerdas no soportan los campos RR, luego la teoría necesita un nuevo objeto fundamental que los soporte, las D-branas.
Los solitones en teoría de cuerdas en 10D corresponden a agujeros negros en una supergravedad 10D (las llamadas branas negras). Estos agujeros negros no rompen la supersimetría, luego son agujeros negros tipo BPS (las D-branas con supersimetría también son de tipo BPS). Las branas tienen cargas eléctricas y pueden tener cargas magnéticas (de tipo Yang-Mills), gracias a la dualidad de Hodge en teorías de campos (de tipo Yang-Mills). Las cargas eléctricas asociadas a los campos de Ramond–Ramond C, CMN y CMNPQ se asocian a la (−1)-brana (instantón-brana), 1-brana y 3-brana, resp., mientras que sus duales de Hodge con cargas magnéticas las asocian a la 7-brana, 5-brana y 3-brana (donde p-brana significa brana negra con volumen del mundo con p+1 dimensiones). Las cargas eléctricas del campo de Kalb–Ramond BMN asociado a las (super)cuerdas tiene como dual de Hodge las cargas magnéticas asociadas a una 5-brana. En resumen, la teoría de supercuerdas de tipo IIB tiene p-branas con p=−1, 1, 3, 5, y 7. El libro no discute las branas de la teoría de tipo IIA (con p=0,2,4,6, y 8), ni de la teoría tipo I (con p=1,5, y 9). Tampoco menciona que las teorías heteróticas no tienen D-branas.
Las D-branas se suelen definir como las regiones del espaciotiempo a las que están ligados los extremos de las cuerdas abiertas. Esta definición es muy poderosa gracias a la dualidad T y nos permite asociar ecuaciones dinámicas para las D-branas, así como cargas eléctricas y magnéticas. Hashimoto discute la dualidad entre Dp-branas y p-branas negras (ambas tipo BPS), y afirmando que «las D-branas son branas» (las teorías Dp-branas de la teoría de supercuerdas tipo IIB con p impar son p-branas (negras) de la teoría de supergravedad tipo IIB, ambas en un espaciotiempo de 10 dimensiones). Finaliza el capítulo con una breve discusión de la dualidad S entre cuerdas y D-branas (solitones), y entre los campos de Kalb–Ramond y de Ramond–Ramond.
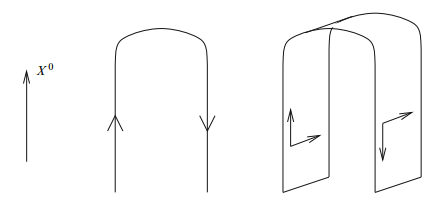
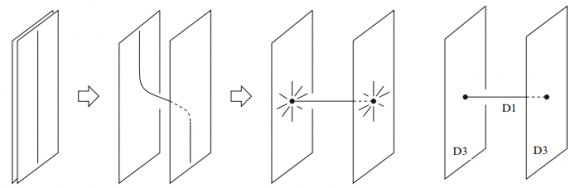
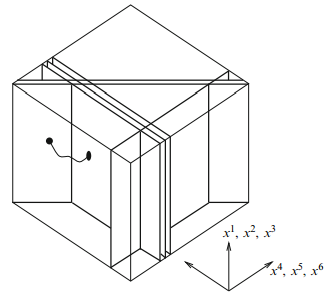
El capítulo 5 «Dynamical D-Branes» (pp. 83-98), discute las ecuaciones que describen el movimiento de las D-branas y sus interacciones mutuas. La masa de los estados de las cuerdas que conectan dos D-branas depende de la distancia mutua entre ellas, siendo cero cuando ambas están superpuestas. De hecho, la posición de los extremos libres de las cuerdas abiertas, que describen el volumen del mundo de la D-brana, se pueden interpretar como campos escalares; estos campos escalares dan cuenta de las vibraciones transversales de las D-branas. La figura de arriba muestra la interpretación de un monopolo magnético como una D1-brana suspendida entre dos D3-branas en un espaciotiempo 3+1 dimensional.
 Las partículas y las antipartículas se pueden aniquilar a pares. Lo mismo ocurre con D-branas de carga opuesta (que podemos llamar aniquilación de una D-brana contra una anti-D-brana). Como las D-branas son solitones topológicos que conectan diferentes estados de vacío (campo de taquiones), su aniquilación mutua corresponde a la transición entre dos estados de vacío (lo que tiene consecuencias cosmológicas a la hora de interpretar la inflación cósmica como interacción entre D- branas). Además, el vacío del campo de taquiones se puede condensar dando lugar a la creación de un par de D-branas (en realidad, D-brana y anti-D-brana). Las D-branas como solitones de la teoría de cuerdas, como branas negras, con una descripción doble, por un lado de tipo gravitatorio y por otro lado de teoría de campos, permite un gran número de aplicaciones del paradigma de la teoría de cuerdas.
Las partículas y las antipartículas se pueden aniquilar a pares. Lo mismo ocurre con D-branas de carga opuesta (que podemos llamar aniquilación de una D-brana contra una anti-D-brana). Como las D-branas son solitones topológicos que conectan diferentes estados de vacío (campo de taquiones), su aniquilación mutua corresponde a la transición entre dos estados de vacío (lo que tiene consecuencias cosmológicas a la hora de interpretar la inflación cósmica como interacción entre D- branas). Además, el vacío del campo de taquiones se puede condensar dando lugar a la creación de un par de D-branas (en realidad, D-brana y anti-D-brana). Las D-branas como solitones de la teoría de cuerdas, como branas negras, con una descripción doble, por un lado de tipo gravitatorio y por otro lado de teoría de campos, permite un gran número de aplicaciones del paradigma de la teoría de cuerdas.
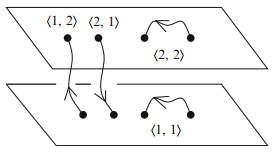
El capítulo 6, «Application of D-Brane Physics» (pp. 99-146), discute las cuatro aplicaciones más conocidas de las D-branas. La primera son los mundos brana (que vivimos en una D3-brana) y su relación con el problema de la jerarquía (recuerda, si hay una teoría de la gran unificación que describe la realidad por debajo, pero cerca, de la escala de Planck, muy alejada de la escala electrodébil, ¿por qué la masa del Higgs no se ve afectada?). Se presenta el modelo ADD de 1998 (Arkani-Hamed, Dimopoulos y Dvali), así como el modelo RS de 1999 (Randall y Sundrum). Estas ideas predicen la existencia de partículas KK con masa 1/R (partículas de Kaluza-Klein) que están siendo buscadas en la escala electrodébil que explora el LHC (aún sin éxito). También se discute la fenomenología del modelo estándar en el contexto de la intersección entre D-branas (ver figura).
La segunda aplicación de las D-branas son los modelos cosmológicos inspirados en la teoría de cuerdas. El campo inflatón es un campo escalar, luego puede ser interpretado como la posición de una D-brana. La inflación surge a partir de la aniquilación de D-branas. Como posible prueba experimental, Hashimoto nos propone la existencia de las cuerdas cósmicas y otros defectos espaciotemporales (cuya existencia, por ahora, está descartada por las observaciones del fondo cósmico de microondas). La tercera aplicación es la física cuántica de los agujeros negros, su termodinámica y entropía vía el análisis de Callan y Maldacena (1996), variante del de Strominger y Vafa (1996), que usa D1-branas y D5-branas en una teoría de supercuerdas tipo IIB.
La cuarta y última aplicación de las D-branas en el libro de Hashimoto es el confinamiento en QCD y la interacción fuerte entre quarks mediada por gluones gracias al principio holográfico de ‘t Hooft y a la correspondencia AdS/CFT de Maldacena. La idea de que la gravedad es un producto de dos teorías de Yang-Mills permite usar solitones clásicos (agujeros negros) para estudiar el acoplo fuerte entre campos cuánticos (en una teoría de Yang-Mills supersimétrica con N colores). La diferencia entre ambas teorías es la dimensión del espaciotiempo subyacente (la gravedad vive en una dimensión más que la teoría de campos, lo que se considera resultado del principio holográfico). Por supuesto, acaba el capítulo recalcando que, todavía, la correspondencia gravedad/gauge es una conjetura y que la supersimetría es una necesidad (QCD es una teoría Yang-Mills basada en SU(3) sin supersimetría, luego la aplicación no permite realizar cálculos detallados, aunque nos ofrece indicios físicos relevantes).
El libro acaba presentando la llamada teoría M (nombre original de Edward Witten) y su posible papel como teoría de todo, que unifica toda la física conocida a escala microscópica. «Toward a Description of Ultimate Theory» (pp. 147-160), capítulo 7, nos aclara que aún no tenemos una definición de lo que es la teoría de cuerdas, «aún no sabemos lo que es,» ya que no conocemos la acción de la teoría M, sus ecuaciones y las simetrías que deben tener sus soluciones; incluso desconocemos el estado vacío de dicha teoría (ni sabemos si es único). Las dualidades T y S nos permiten conectar las teorías de cuerdas en 10D con la teoría M en 11D, pero sólo en ciertos límites. Las D-branas son fenómenos no perturbativos en teoría de cuerdas, pero aún no conoemos la formulación no perturbativa definitiva de la teoría M.
Hashimoto destaca que necesitamos una teoría cuántica de la gravedad para entender la naturaleza cuántica del espaciotiempo, es decir, cómo emerge el espaciotiempo clásico con cierto número de dimensiones a partir de la interacción objetos más fundamentales. La dualidad T nos sugiere que el concepto de dimensión en teoría de cuerdas es emergente, ya que hace equivalente Dp-branas (con p dimensiones espaciales) con D(p+1)-branas y con D(p−1)-branas según la compactificación considerada para las dimensiones extra. Acaba el capítulo presentando la idea de la teoría de la matriz (cuerdas que conectan D0-branas, es decir, gravitones KK), pero deja claro que no sabemos generalizar la idea a otras Dp-branas.
En los últimos 50 años la teoría de cuerdas ha cambiado como ninguna otra teoría física lo ha hecho en tan poco tiempo. Los avances son continuos y cada día entendemos mejor el zoo de soluciones fundamentales de la teoría y sus interacciones. Sin embargo, aún no conocemos su formulación definitiva y su vacío (la física a baja energía que nos rodea), si es que existe uno único (problema del paisaje de vacíos o landscape); Hashimoto se decanta por la teoría cuántica de campos cuerdísticos (string field theory), pero queda mucho trabajo por realizar para desvelar todos sus secretos. Acaba el libro con la frase «en el siglo XXI, la teoría de cuerdas y las D-branas han dado un nuevo paso hacia adelante, y empiezan a abrir nuevas puertas para la física.»









Sorprende la claridad de la expresión escrita de Koji Hashimoto en las pizarras…
Si no supone mucho esfuerzo ¿sería posible un post en que se comentase qué ascpectos concretos de las diversas teorías en competencia (gravedad cuántica, supercuerdas, etc.) pueden dilucidarse empleando los recursos del LHC?
Vicente, la gravedad cuántica y la teoría de supercuerdas son teorías a una escala de energía que el LHC no puede explorar. Luego el LHC no puede aportar nada en firme sobre ellas. Sin embargo, estas teorías han inspirado ideas a baja energía (fenomenología) que se puede explorar con el LHC: nuevas partículas (hay decenas de variantes, desde partículas supersimétricas, partículas de Kaluza-Klein, nuevas simetrías gauge (W’,Z’,etc.), nuevas partículas escalares, fermiones vectoriales, etc.).
Lo importante que debes saber es que el LHC no tiene por objetivo estudiar la gravedad cuántica o las supercuerdas. Cualquier nuevo descubrimiento que haga no se puede interpretar en ningún caso como confirmación de estas teorías. La teoría de supercuerdas «predice» el Higgs (toda una familia de Higgs), pero no podemos interpretar su descubrimiento como apoyo experimental a esta teoría (pues casi todas las teorías que existen predicen familias de partículas tipo Higgs).
Lo que está claro es que la evolución de la física teórica no se acaba en la teoría de cuerdas, sino que ésta es solo un paradigma más, en competición con otros, en el camino hacia la resolución del gran problema de la gravedad cuántica. Lo más probable es que el nuevo paradigma que haga esto, la teoría que sea adoptada por toda la comunidad de la física teórica, sea una teoría completamente distinta a la teoría de cuerdas. Es decir, yo apostaría que la validez de la teoría de cuerdas será medida por su aportación más o menos importante en la construcción de este nuevo paradigma. Nuevo paradigma que mostrará su validez en dos direcciones, a saber, la teoría convergerá a la realidad pero también la realidad convergerá a la teoría. Es claro que la teoría de cuerdas hasta el momento no ha hecho esto. Por tanto dejaremos la suerte de la teoría cuerdas al juicio de la historia.