El principio de indeterminación de Heisenberg limita la precisión en las medidas simultáneas de dos observables que no conmutan entre sí. El squeezing es una técnica que permite mejorar la precisión de uno de los observables a costa de empeorarla en el otro. En sistemas de átomos de rubidio entrelazados se ha logrado una «compresión» de espín que reduce el ruido en 20 decibelios (dB), es decir, en un factor de cien. Todo un récord que duplica los 10 dB (un factor de 11) logrados el año pasado.
El logro tiene aplicaciones en el desarrollo de relojes atómicos más precisos, sensores inerciales y en experimentos de física fundamental. Hay que recordar que los estados «comprimidos» con fotones se usan para reducir el error en los interferómetros para la detección de ondas gravitacionales. Tanto en GEO-600 como LIGO se ha logrado reducir el ruido en 2,5 dB. Futuros avances en metrología con fotones «comprimidos» permitirán reducir aún más este ruido de fondo.
El artículo es Onur Hosten et al., «Measurement noise 100 times lower than the quantum-projection limit using entangled atoms,» Nature (11 Jan 2016), doi: 10.1038/nature16176.
El principio de indeterminación de Heisenberg afirma que para dos observables A y B en un espacio de Hilbert se tiene que (∆A)²(∆B)² ≥ |<[A,B]>|²/4, donde la varianza (∆O)²=<O²>−<O>², y el conmutador [A,B]=AB−BA. Se llama límite de ruido cuántico estándar al valor de la varianza que satura la desigualdad, es decir, (∆A)² = (∆B)² = |<[A,B]>|²/2. Un estado cuántico está «comprimido» (squeezed en inglés) para el operador A cuando su varianza es menor que el límite de ruido cuántico estándar, por ejemplo, (∆A)² < |<[A,B]>|²/2; en dicho caso es obvio que para el otro operador B se tendrá (∆B)² > |<[A,B]>|²/2.
El concepto de «compresión» (squeezing) se puede extender a N operadores, o lo que es lo mismo, a un único operador aplicado a N sistemas cuánticos idénticos que estén entrelazados entre sí. Los estados «comprimidos» entre N bosones (normalmente fotones) se usan mucho en metrología cuántica porque permiten reducir el ruido cuántico estándar hasta en un factor 1/N. Se ha logrado reducir el ruido cuántico hasta en 12 dB usando fotones. Sus aplicaciones son múltiples, por ejemplo, se usan para reducir el ruido cuántico en los interferómetros de los detectores de ondas gravitacionales (en GEO-600 y LIGO se ha logrado una reducción de 2,5 dB).
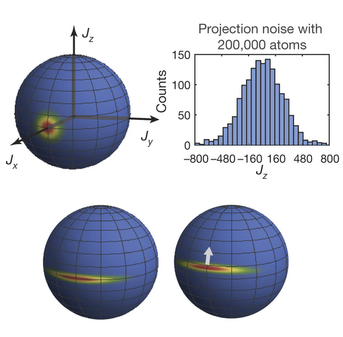
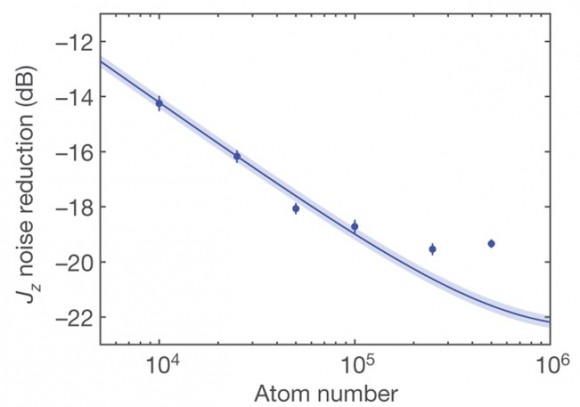
En ciertas aplicaciones en metrología cuántica interesa usar la «compresión» en sistemas atómicos, en concreto, en su espín (los llamados estados de espín «comprimido» o spin-squeezed states). Un sistema de N átomos con dos niveles electrónicos (cada uno con espín 1/2) entrelazados entre sí se comporta como un «átomo gigante» con espín J=N/2. Las tres componentes del espín J = (Jx, Jy, Jz) cumplen la relación de indeterminación ∆Jz ∆Jy ≥ |<Jx>|/2 (y sus combinaciones de índices). El límite de ruido cuántico estándar se cumple cuando ∆Jz = ∆Jy = √N/2. Los estados «comprimidos» permiten reducir la varianza de una de las componentes del espín hasta ∆Jz < |<Jx>|/√N. Usando átomos de Rb-87 en cavidades ópticas se había logrado una reducción de hasta 10 dB en el ruido cuántico (es decir, un factor de 11). El nuevo trabajo publicado en Nature logra una reducción de hasta 20,1 ± 0,3 dB, es decir, un factor de 100.
En el experimento se han atrapado unos 500 mil átomos de Rb-87 que se han entrelazado mediante pulsos ópticos adecuados. Por supuesto, ha sido imposible entrelazar todos los átomos. El resultado obtenido permite asegurar que al menos 680 ± 35 átomos han sido entrelazados. Lo curioso de esta técnica es que permite usarse a la inversa, es decir, para estimar el número de átomos entrelazados en un conjunto de átomos atrapados en una trampa óptica, lo que tiene aplicaciones en computación cuántica. Pero en el nuevo artículo se limitan a desarrollar un reloj atómico 11 veces más preciso (reducen el error en 10,5 ± 0,3 dB).
Futuras mejoras en la técnica desarrollada permitirán un entrelazamiento de un mayor número de átomos y un incremento en el número de decibelios de reducción de ruido en las medidas.




Hola, Francis:
¿Qué piensas de los rumores de que el LIGO ha descubierto ondas gravitatorias?
Off-topic: De momento solo rumores. Me parece que podría ser relevante esto:
» … there is the other possible scenario: that the researchers have seen a false signal planted deliberately as a drill. The LIGO is almost unique among physics experiments in practising ‘blind injection’. A team of three collaboration members has the ability to simulate a detection by using actuators to move the mirrors. “Only they know if, and when, a certain type of signal has been injected,” says Laura Cadonati, a physicist at the Georgia Institute of Technology in Atlanta who leads the Advanced LIGO’s data-analysis team.
Two such exercises took place during earlier science runs of LIGO, one in 2007 and one in 2010. … »
Leído aquí:
http://www.nature.com/news/has-giant-ligo-experiment-seen-gravitational-waves-1.18449
Pero ojalá no sea eso y el descubrimiento se confirme, saludos.
Yo también lo vi anteayer y espero que sea algo real y más que rumores a diferencia de lo que acabó pasando con BICEP2. A ver si Francis puede comentar algo más.
Falsa alarma. Similar a «Big Dog» la señal que LIGO observó en septiembre de 2010. Hubo muchos rumores. Hasta marzo de 2011 no se supo la verdad: «blind injection (test)».
El 14 de marzo de 2011 se convocó en privado a toda la colaboración para preparar el anuncio oficial público de la primera onda gravitacional. Todos, salvo 2 o 3 personas, ignoraban que la señal había sido inyectada el 16 de septiembre de 2010 de forma artificial. La idea era entrenar a los miembros para un futuro anuncio real. En el último minuto de la conferencia se desveló el secreto. Falsa alarma.
En septiembre de 2015, Advanced LIGO inició su toma de datos. Y en septiembre de 2015 se observó una señal. Los rumores (iniciados por Krauss) corrieron como la pólvora. Ahora en enero vuelven a correr los rumores (de nuevo con el marchamo de Krauss). ¿Señal real? ¿Nueva señal ficticia?
En 2010-2011 fueron necesatios 18 meses de análisis para que los rumores se quedaran en «lo siento, falsa alarma». Este año calculo que se necesitará la mitad de tiempo (unos 9 meses). Luego me atrevo a calcular que este verano sabremos si el cuento de «Pedro y el lobo» se ha vuelto a repetir, o si estamos ante un posible Premio Nobel para 2018.
Saludos
Gracias. Habrá que esperar…
Lástima. Gracias por aclararlo.
Francis, ¿has visto estos nuevos rumores que han aparecido hoy?
https://www.newscientist.com/article/2076754-latest-rumour-of-gravitational-waves-is-probably-true-this-time/
Saludos
En
«El principio de indeterminación de Heisenberg limita la precisión en las medidas simultáneas de dos observables que conmutan entre sí»
¿debería ser
«El principio de indeterminación de Heisenberg limita la precisión en las medidas simultáneas de dos observables que no conmutan entre sí»
?
¿o no es estoy entendiendo correctamente
Mecánica cuántica from a dummy. Que no te lo cuenten 7
?
Gracias, Gervasio.