En el grafeno se propagan cuasipartículas de tipo fermión de Dirac sin masa. ¿Se puede observar su función de onda? Para ello habría que confinarlas en una trampa. Se publican dos artículos en Nature Physics que usan un punto cuántico para atrapar estas cuasipartículas y observarlas con un microscopio de efecto túnel (STM). Gracias a ello han podido medir la función de onda asociada a estas cuasipartículas, eso sí, en un estado confinado (semiestable).
Los fermiones de Dirac sin masa muestran la paradoja de Klein, un efecto túnel sin reflexión que impide atraparlos. Para lograrlo hay que construir un punto cuántico, una unión p–n en el grafeno con forma circular. Dicho punto cuántico actúa como un potencial que mueve el nivel de Fermi por encima (fuera del punto) y por debajo (dentro del punto) de la energía asociada a los vértices de los conos de Dirac en el grafeno.
Un gran trabajo experimental que han permitido los avances en las técnicas de fabricación de dispositivos basados en grafeno. Los artículos son Christopher Gutiérrez, Lola Brown, …, Abhay N. Pasupathy, «Klein tunnelling and electron trapping in nanometre-scale graphene quantum dots,» Nature Physics (27 Jun 2016), doi: 10.1038/NPHYS3806, y Juwon Lee, Dillon Wong, …, Michael F. Crommie, «Imaging electrostatically confined Dirac fermions in graphene quantum dots, » Nature Physics (27 Jun 2016), doi: 10.1038/NPHYS3805. Recomiendo también leer a Heejun Yang, «Graphene traps,» News & Views, Nature Physics (27 Jun 2016), doi: 10.1038/nphys3817.
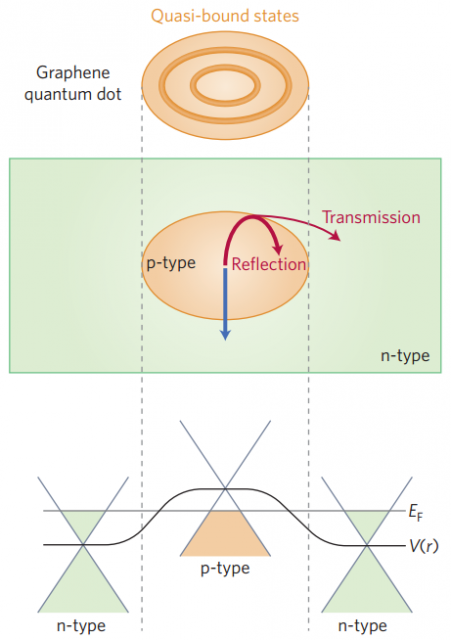
Esta figura ilustra de forma esquemática cómo el punto cuántico atrapa a las cuasipartículas. La paradoja de Klein afirma que los fermiones sin masa atraviesan una barrera de potencial en dirección normal con probabilidad igual a la unidad (sin reflexión, solo transmisión), como indica la flecha azul. Pero también afirma que las que inciden en la barrera con grandes ángulos lo hacen con probabilidad casi nula (sin transmisión, solo reflexión), como ilustra la flecha roja.
La forma circular del punto cuántico dota a las quasipartículas de momento angular. Las que tienen un gran momento angular colisionan en el contorno del punto con grandes ángulos. Tras múltiples rebotes en el contorno, se logra atrapar a dichas cuasipartículas en el punto cuántico, al menos de forma temporal (se trata de un estado cuasi-ligado que es metaestable).
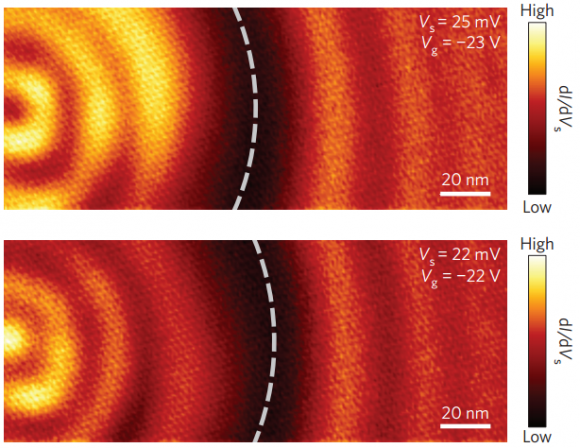
Usando la punta de un microscopio de efecto túnel (scanning tunneling microscope) se puede determinar la forma de la función de onda de los fermiones de Dirac sin masa atrapados en el punto cuántico. Dicha función de onda se observa como nodos y antinodos con simetría circular, muy similares a la onda que se produce en la superficie del agua cuando tiramos una piedra, pero estacionaria (ya que está atrapada por el punto cuántico).
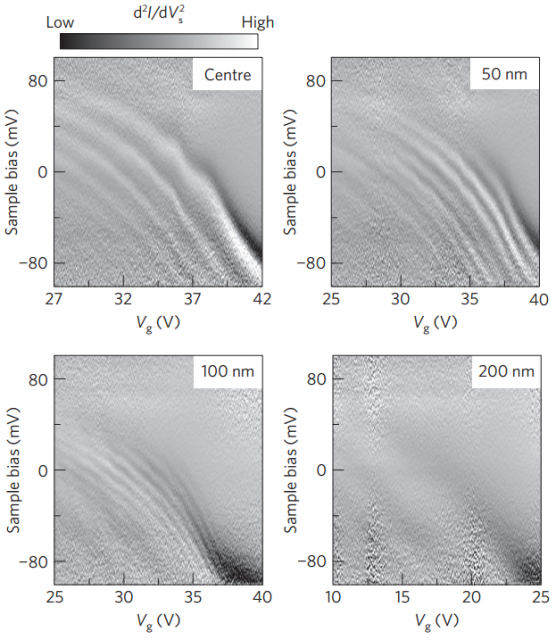
El estado confinado es metaestable (cuasi-ligado) con una vida media de unos ~10 femtosegundos. Por ello se han tomado las imágenes de la función de onda en varios puntos a lo largo del radio del punto cuántico. Los resultados son todo un alarde técnico, como puedes imaginar, pero son realmente espectaculares.
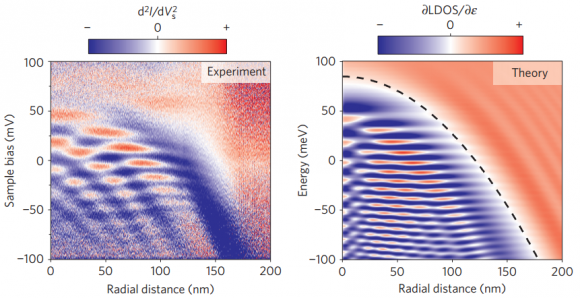
Hasta ahora se había podido explorar la naturaleza como fermiones de Dirac sin masa para las cuasipartículas de electrones en el grafeno por métods indirectos. Dichos métodos confirmaron su existencia fuera de toda duda. Pero poder observar sus funciones de onda es sin lugar a dudas un paso de gigante. Ya he dicho que son resultados espectaculares, pero me reitero. Por supuesto, se han confrontado los resultados experimentales con las predicciones teóricas y se comprobado que están en completo acuerdo.
También se ha podido medir la distribución espacial del espectro energético de las cuasipartículas dentro del punto cuántico. El resultado también está en buen acuerdo con las predicciones téoricas. Hay que recordar que la precisión espacial de la punta del microscopio de efecto túnel limita los detalles que se pueden observar. Pero si se tiene en cuenta el efecto del aliasing debido a la frecuencia de muestreo el resultado es muy bueno.
Los dos artículos en Nature Physics han observado el mismo fenómeno, pero hay varias diferencias entre ellos. La más importante es que se han usado dos técnicas diferentes para fabricar el punto cuántico. Lee et al. han obtenido un perfil parabólico, con bordes más suaves. Gutiérrez et al. han logrado un perfil más plano en el centro y con bordes muy marcados. Como resultado, las amplitudes y los perfiles de las funciones de onda observadas difieren. Pero ambos casos, al compararlas con las predicciones teóricas obtenidas con simulaciones por ordenador se obtiene un acuerdo excelente.
En resumen, hace unas semanas en la conferencia científica NoLineal 2016 en Sevilla le comenté a una colega que aún no se habían observado de forma directa los fermiones de Dirac sin masa en el grafeno, pero que quedaba poco para que se lograra. Por poco yo quería decir pocos años. Quizás ella esté pensando ahora mismo que por poco yo me refería a unas semanas. La ciencia avanza que es una barbaridad.