La teoría de la información permite mirar con nuevos ojos la mecánica cuántica. Un buen ejemplo es el reciente análisis de la computación cuántica contrafáctica en interferómetros de Mach–Zehnder anidados. La información mutua de Shannon mide la cantidad de información transmitida en un canal con ruido, mientras la información de Fisher mide la incertidumbre en el mensaje causada por dicho ruido. Usando estos conceptos se puede medir el grado de contrafacticidad (counterfactuality) de un protocolo cuántico. Gracias a ellos se observa que algunos protocolos recientes son contrafácticos solo en un canal cuántico perfecto, siendo su grado de contrafacticidad despreciable en la práctica.
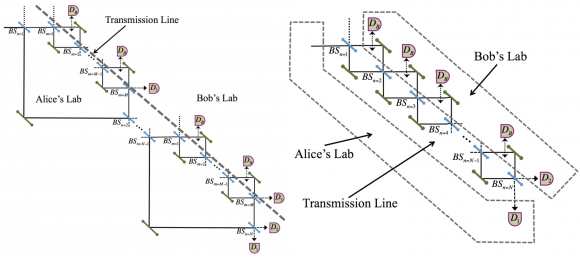
El interesante artículo es D. R. M. Arvidsson-Shukur, A. N. O. Gottfries, C. H. W. Barnes, «Evaluation of Counterfactuality in Counterfactual Communication Protocols,» Phys. Rev. A 96: 062316 (18 Dec 2017), doi: 10.1103/PhysRevA.96.062316, arXiv:1705.06574 [quant-ph]. Se analizan dos protocolos concretos, resultando que solo funciona en canales con ruido (líneas de transmisión) el propuesto por los propios autores en D. R. M. Arvidsson-Shukur, C. H. W. Barnes, «Quantum Counterfactual Communication Without a Weak Trace,» Phys. Rev. A 94: 062303 (2016), doi: 10.1103/PhysRevA.94.062303, arXiv:1705.05628 [quant-ph], solo funcionando en canales perfectos (sin ruido) el de Hatim Salih, Zheng-Hong Li, …, M. Suhail Zubairy, «Protocol for direct counterfactual quantum communication,» Phys. Rev. Lett. 110: 170502 (2013), doi: 10.1103/PhysRevLett.110.170502, arXiv:1206.2042 [quant-ph].
El nuevo análisis permite entender por qué no pueden funcionar en la práctica protocolos de clonado cuántico contrafáctico como el presentado en Qi Guo, Shuqin Zhai, …, Shou Zhang, «Counterfactual quantum cloning without transmitting any physical particles,» Phys. Rev. A 96: 052335 (27 Nov 2017), doi: 10.1103/PhysRevA.96.052335; por ello recomiendo su lectura a todos los físicos jóvenes interesados en la física cuántica en general y en la computación contrafáctica en particular.
Entre las escapatorias (loopholes) más famosas a los resultados de los experimentos tipo Bell está la escapatoria del juego limpio (fair sampling loophole), asociada a la a la eficiencia de los detectores (que nunca alcanza el 100% ideal). En el contexto de la computación cuántica contrafáctica esta escapatoria se asocia a un canal perfecto (sin ruido); como no existen estos canales ideales, se descartan las paradojas asociadas a la interpretación de las medidas contrafácticas. El uso de la teoría de la información permite superar esta escapatoria y medir el grado de contrafacticidad como función del ruido del canal (que suele ser una línea de transmisión).
Entrar en los detalles del nuevo trabajo de Arvidsson-Shukur y sus colegas nos llevaría lejos, pues la mayoría de los lectores no recordarán que es la computación contrafáctica (el artículo de está muy bien escrito y será fácil de leer para casi todos los físicos y buenos aficionados a la física cuántica). Permíteme un recordatorio rápido de lo que es la computación contrafáctica. Roger Penrose introdujo las medidas contrafácticas en alusión al concepto de condicional contrafáctico que se usa en Filosofía. La idea es usar la no-localidad cuántica para medir alguna cosa que habría podido suceder, pero que nunca tuvo lugar. En la práctica se trata de combinar en un mismo experimento medidas de tipo partícula con medidas tipo onda usando interferómetros anidados.
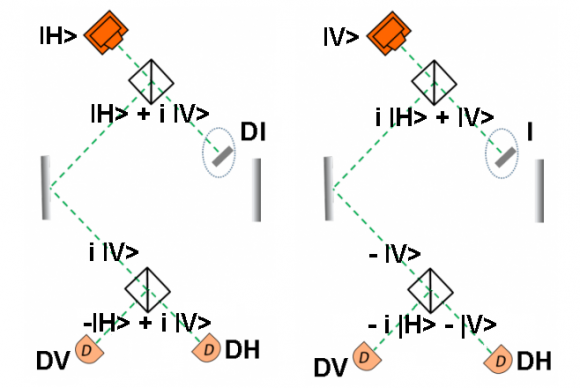
Imagina que tienes un generador de fotones en dos estados posibles, sean |H> y |V>, en la parte de arriba de la figura. Además, tenemos tres detectores, sean DI, DV y DH. En ausencia del detector DI, el estado |H> provoca una señal en el detector DH y ninguna señal en el detector DV (parte izquierda de la figura), y el estado |V> provoca una señal en el detector DV y ninguna señal en el detector DH (parte derecha de la figura).
En la figura aparecen divisores de haz (arriba y abajo), que realizan la operación |H> → |H> + i |V> y la operación |V> → i |H> + |V>, donde i = eiπ/2 = √−1, y se han omitido términos de normalización 1/√2 (incómodos de escribir en HTML). Los espejos (a la derecha y a la izquierda) realizan la operación |H> → i |V> y la operación |V> → i |H>.
Asumamos que tenemos los tres detectores, pero que DI no detecta la partícula (algo que ocurre el 50% de las veces), por tanto, ignoramos por qué camino se mueve la partícula. Para el estado |H> tras el divisor de haz de arriba (parte izquierda de la figura) se tiene el estado |H> + i |V>; que tras reflejarse en los dos espejos el estado es −|H> + i |V> justo antes de llegar el divisor de haz de abajo donde resulta el estado −|H>, que produce una señal el 100% de las veces en el detector DH y ninguna señal en el detector DV (cuya señal no depende del signo ya que su medida depende del cuadrado del estado <H|H>).
Por otro lado, si el estado de partida hubiera sido el |V> tras el divisor de haz de arriba (parte derecha de la figura) se tendría el estado i |H> + i |V>; que tras reflejarse en los dos espejos el estado es i|H> − |V> justo antes de llegar el divisor de haz de abajo donde resulta el estado −|V>, que produce una señal el 100% de las veces en el detector DV y ninguna señal en el detector DH (recuerda que la medida depende de <V|V>).
Este figura ilustra los otros dos casos posibles, cuando el detector DI detecta la partícula (algo que ocurre el 50% de las veces); en un análisis clásico uno esperaría que los detectores DV y DH no detectaran ninguna señal, porque la partícula se propagaba por el camino derecho y el detector DI ha impedido que alcance el espejo derecho; por el camino izquierdo no se propaga ninguna partícula. Sin embargo, un análisis cuántico es un poco más sutil, aunque sencillo.
La parte izquierda de la figura muestra lo que pasa para el estado de partida |H>; tras el divisor de haz de arriba se tiene el estado |H> + i |V> antes de llegar a DI; en el espejo izquierdo se refleja el estado |H> dando como resultado el estado i |V>, que incide en el divisor de haz de abajo donde resulta el estado −|H>+i |V>, que produce una señal el 25% de las veces en el detector DH y el 25% de las veces en el detector DV.
La parte derecha de la figura muestra lo que pasa si el estado de partida hubiera sido el |V>; tras el divisor de haz de arriba se tendría el estado i |H> + |V> que tras reflejarse en el espejo izquierdo pasa al estado −|V>, que tras pasar por el divisor de haz de abajo resulta en −i|H> − |V>, que produce una señal el 25% de las veces en el detector DH y el 25% de las veces en el detector DV.
Por tanto, si al enviar una partícula en el estado DH (o DV) se activa el detector DV (o DH) entonces sabemos que la partícula ha dado una señal en el detector DI; se habrá realizado una medida contrafáctica, porque no debería haber ocurrido (según un análisis clásico ya que hay señal en DI), pero que podría haber ocurrido (pues si algo ha activado el detector debería ser una partícula).
En resumen, las matemáticas de la física cuántica son muy sencillas, si uno opera con ellas olvidando su intuición clásica. Lo que ocurre con estos experimentos ideales es que al realizarlos en un laboratorio hay gran número de fuentes de ruido que falsean los resultados. Por ello resulta muy interesante contar con una medida de la contrafacticidad, como la propuesta en el nuevo artículo de Arvidsson-Shukur y sus colegas. Así en la práctica podemos saber cuán próximos están nuestros resultados a los esperados en un caso ideal. Cuando muchos físicos se acostumbren a esta medida, como revisores de nuevos artículos, exigirán que se incluya la oportuna cuantificación de la contrafacticidad. Tiempo al tiempo.




Feliz año al autor del blog, gracias por los regalos diarios que nos haces en forma de conocimiento y entretenimiento y gracias por la paciencia que tienes contestando los comentarios de gente como yo que muchas veces preguntamos obviedades.
Y feliz año también al resto de lectores y comentaristas.
Una obra reciente, que circula como adelanto en Buenos Aires, dice al respecto: «al causar su efecto, en este efecto la causa se aniquila. /…/. De donde surge otra “ley” natural o regularidad predictiva de la naturaleza: por esa aniquilación la física prohíbe a todo efecto mantener referencia física o relación natural al evento singular que lo plasmó.
Sin embargo, suponer lo contrario es una superstición típica de la anglofonía, así como de la doctrina homeopática. Un reciente ejemplo académico declara: “we make the assumption that any realistic quantum channel in MZI [Mach-Zehnder interferometers] structures will have some weak uncontrolled interaction” . Periodistas menos concienzudos lo difunden como “los físicos de Cambridge han conseguido demostrar, en efecto, que el modo en que las partículas interactúan con su entorno deja en ellas una «huella» que puede ser rastreada a posteriori en laboratorio, en el momento de la observación.” Reveladoramente agregan: “Los investigadores partieron de la idea de que cualquier partícula no puede, en ningún momento, dejar de interactuar con su entorno, y que esa interacción la irá «marcando» a lo largo de su recorrido. De esta forma, Arvidsson-Shukur y su equipo idearon un método para que los científicos pudieran «mapear» esas interacciones a posteriori y sin necesidad de estar observando las partículas continuamente.” ¿Quién dijo que ya no queda manera de que presenciemos la muerte de Sócrates, los acontecimientos del Gólgota en tiempos de Pilatos, el asesinato de John Kennedy o el umbroso derrumbe de las Torres Gemelas? Los futuros magistrados penales podrán por fin ser infalibles. Endemientras, el investigador principal asevera que “asumimos el desafío de crear una forma de rastrear los movimientos secretos de las partículas cuánticas … con nuestro trabajo hemos sido capaces de explorar el ‘dominio prohibido’ de la mecánica cuántica: conocer el camino de las partículas cuánticas cuando nadie las está observando”. Ni se le viene a mientes que debiera explicar por qué “we made the assumption”.
Eppur´, tal asunción es una mera superstición, culturalmente difundida. Los hechos de la naturaleza le son incompatibles. Cuando una pluralidad de eventos singulares se integra en causar un rastro, por ejemplo una huella de tigre americano, o cierto estado (o “sistema”) de todos los componentes físicos del hierro de la [mencionada] locomotora en un instante histórico determinado, la aniquilación de cada previo evento causativo microfísico se integra en la aniquilación, de la relación física de todos ellos, con la huella dejada en la tierra o la locomotora a punto de partir, tremando bochinchera entre silbos y vapor.
Dicha aniquilación física exige forzosamente concebir cualquier “huella que haga memorizar”, o rastro recordatorio, como diferenciaciones internas de alguna existencialidad, sin la cual su información física no podría mantener relación unívoca con el evento que la plasmó. Ha de ser un psiquismo, que intelige por propia experiencia causal, el que debe imaginarle aquella relación causal en la que ya no se involucra.»
Mil gracias por tus publicaciones periodicas, soy medico y muy interesado en lo tuyo. Feliz Año 2018!!!