Los cristales de tiempo de Wilczek, propuestos por este Premio Nobel en 2012, no existen en la Naturaleza. Sin embargo, muchos cristales en los que se inyecta energía de forma periódica se comportan como cristales de tiempo de Floquet. En ellos aparece una rotura espontánea de la simetría de traslación temporal (la energía no se conserva) gracias al forzamiento externo (la inyección de energía). Dos artículos en Physical Review Letters publican nuevos materiales en los que se ha observado este comportamiento (que sigue siendo difícil de observar de forma experimental). Por un lado, cristales de dihidrógeno fosfato de amonio (MAP) y, por otro lado, varios líquidos cuyas moléculas se comportan como racimos estrellados de espines nucleares. En ambos casos la señal parece clara. Pronto se observará en muchos otros materiales.
Los aficionados a los cómics de Marvel, tras leer cristal de tiempo, pensarán en una gema del infinito, la gema-tiempo cuyo portador adquiere la habilidad de controlar el tiempo. Máxime tras el reciente estreno de la película «Vengadores: Infinity War» (04 May 2018). Nada más lejos de la realidad. Un cristal (convencional) tiene una estructura regular que se repite en el espacio y que rompe la simetría de traslación espacial; un cristal de tiempo tiene un comportamiento oscilatorio forzado que se repite en el tiempo y que bajo ciertas circunstancias rompe la simetría de traslación temporal. En lugar de usarse el término oscilador forzado, a secas, que todo el mundo conoce de sus estudios sobre la resonancia, se usa el término cristal de tiempo cuando la oscilación se desacopla del forzamiento bajo ciertas circunstancias (como si hubiera un comportamiento similar al resonante, pero fuera de la resonancia).
Ya se conocen varios materiales que se comportan como cristales de tiempo de Floquet bajo ciertas circunstancias. Todavía sigue siendo noticia los nuevos descubrimientos (acabarán dejando de serlo en poco tiempo). Los nuevos artículos son Jared Rovny, Robert L. Blum, Sean E. Barrett, «Observation of Discrete-Time-Crystal Signatures in an Ordered Dipolar Many-Body System,» Phys. Rev. Lett. 120: 180603 (01 May 2018), doi: 10.1103/PhysRevLett.120.180603; Jared Rovny, Robert L. Blum, Sean E. Barrett, «31P NMR study of discrete time-crystalline signatures in an ordered crystal of ammonium dihydrogen phosphate,»
Phys. Rev. B 97: 184301 (01 May 2018), doi: 10.1103/PhysRevB.97.184301; y Soham Pal, Naveen Nishad, …, G. J. Sreejith, «Temporal Order in Periodically Driven Spins in Star-Shaped Clusters,» Phys. Rev. Lett. 120: 180602 (01 May 2018), doi: 10.1103/PhysRevLett.120.180602.
Más información divulgativa en Michael Schirber, «Synopsis: Time Crystals Multiply,» Physics, 01 May 2018; Emily Conover, «‘Time crystals’ created in two new types of materials,» ScienceNews, 04 May 2018; Jim Shelton, «Yale physicists find signs of a time crystal,» Yale News, 02 May 2018.
En este blog también puedes leer «Frank Wilczek propone la existencia de cristales de tiempo», LCMF 16 Oct 2012; «La polémica de los cristales de tiempo», LCMF, 10 Ene 2013; «Nueva propuesta teórica para observar cristales de tiempo», LCMF, 15 Abr 2014; «Físicos afirman haber creado el primer cristal de tiempo discreto», LCMF, 08 Oct 2016; «Cristales de tiempo de Floquet», LCMF, 11 Mar 2017.
Un cristal de tiempo de Floquet, también llamado cristal de tiempo discreto (DTC), es un sistema oscilatorio hamiltoniano (que conserva la energía) en el que se aplica un forzamiento externo y una fuente de disipación (pérdida de energía). La teoría de la resonancia indica que las oscilaciones del sistema decaen a una frecuencia igual a la mitad de la frecuencia de forzamiento; fuera de la resonancia el sistema presenta batidos a dos frecuencias por debajo y por encima de dicha frecuencia. Sin embargo, en un DTC hay una frecuencia a partir de la cual el sistema deja de presentar estos batidos y recupera la frecuencia original; este fenómeno es resultado de la rotura de la simetría ante traslaciones en el tiempo inducida por la disipación (recuerda que según el teorema de Noether esta simetría está detrás de la conservación de la energía). Por supuesto, un cristal de tiempo de Floquet no tiene nada que ver con un cristal de tiempo de Wilczek, pues este último es un sistema físico prohibido por las leyes de la termodinámica; a pesar de ello se usa el término «cristal de tiempo» porque es muy sexy.
En el experimento del grupo de Yale se usa fosfato monoamónico (MAP), hasta ahora se habían fabricado cristales de tiempo discretos basados en iones de iterbio atrapados y en defectos de nitrógeno en cristales de diamante. El MAP es un material barato que se usa en muchos juguetes científicos para niños para ilustrar el crecimiento de cristales cuya fórmulas es NH4H2PO4. En los experimentos se usa un equipo de resonancia magnética nuclear (NMR) para explorar las oscilaciones del espín de los átomos de fósforo (31P) en el MAP.
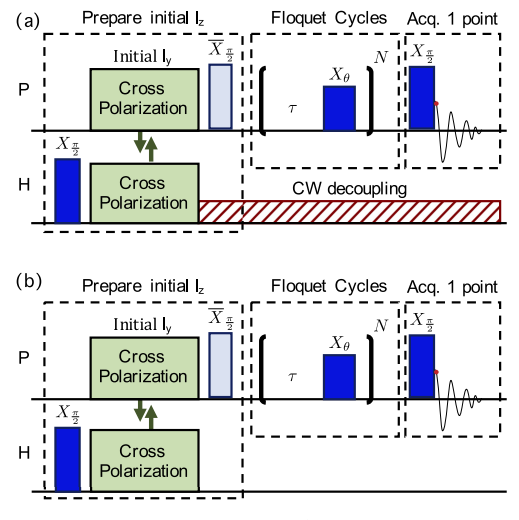
Se prepara los espines de 31P en un estado +z débilmente polarizado (se parte de un estado +y al que se aplica un pulso magnético que lo rota al eje z). Este estado se relaja en unos 0.6 segundos, tiempo durante el cual se aplica una secuencia de pulsos separados por un tiempo de espera τ que rotan el sistema respecto al eje +x en un ángulo θ. Para N=1, 2, …, 128, se repite una medida tras N pulsos (ciclos de Floquet) en la que se observa mediante NMR la magnetización en el eje z (puntos azules para N par y verdes para N impar). El resultado es una señal oscilatoria cuya envolvente decae a la que se le aplica la transformada de Fourier para determinar su espectro.
Para τ pequeño y θ ≈ π el sistema responde oscilando a la mitad de la frecuencia de forzamiento, ν = 1/2 (véase la parte (a) de la figura). Cuando θ se aleja del valor π, la respuesta del sistema presenta batidos con una frecuencia determinada por θ − π (véase la parte (b) de la figura). Este resultado es el esperado para un oscilador forzado. El comportamiento como cristal de tiempo aparece para θ ≠ π cuando se incrementan los valores de τ (veáse la parte (c) de la figura); de forma inesperada el sistema retorna a la frecuencia ν = 1/2, lo que se interpreta como una señal del comportamiento como cristal de tiempo discreto.
El grupo de Yale ha demostrado que este comportamiento es robusto. Al repetir el experimentos múltiples veces con diferentes tiempos de espera τ se observa que los resultados (triángulos rojos en esta figura) decaen por debajo de la curva de caída asociada al comportamiento oscilatorio disipativo del sistema (curva negra continua en la figura). Este resultado concuerda con el esperado para un cristal de tiempo discreto.
En el artículo de los físicos indios se usa un procedimiento similar para ilustrar el comportamiento como cristal de tiempo de cristales de acetonitrilo (CH3CN), fosfito de trimetilo (P(OCH3)3) y tetrakis(trimetilsilil)silano ([(CH3)3Si]4Si). Sin entrar en más detalles, se observa el mismo tipo de comportamiento como cristal de tiempo discreto para estos tres cristales. Por tanto, ahora se conocen seis materiales que son cristales de tiempo de Floquet. Sin lugar a dudas, en los próximos meses, aparecerán muchísimos más.