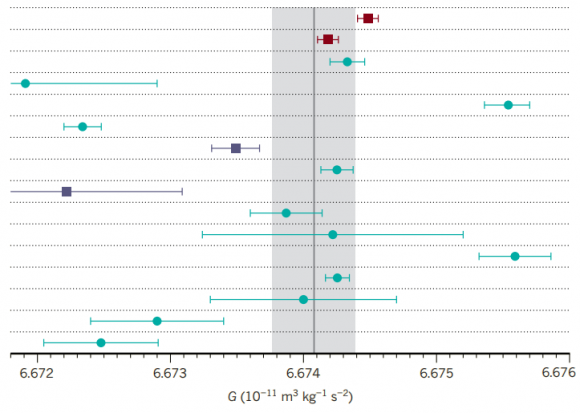
Medir la constante de gravitación universal de Newton es muy difícil; por ello su valor es uno de los más imprecisos de todas las constantes fundamentales. Científicos chinos han publicado en Nature las dos medidas más precisas hasta ahora, usando sendos péndulos de torsión. Los valores obtenidos son G = 6.674 184(12) × 10−11 m³/kg/s², y G = 6.674 484(12) × 10−11 m³/kg/s². Difieren entre sí a casi 4 sigmas, pero son compatibles a menos de dos sigmas con el valor CODATA 2014 de G = 6.674 08(31) × 10−11 m³/kg/s². No se conoce la razón de la discrepancia, que podría ocultar nueva física; pero lo más razonable es que la causa sean efectos sistemáticos no entendidos en alguno de los dos experimentos. Futuros estudios tendrán que clarificar esta cuestión.
El artículo es Qing Li, Chao Xue, …, Jun Luo, «Measurements of the gravitational constant using two independent methods,» Nature 560: 582–588 (29 Aug 2018), doi: 10.1038/s41586-018-0431-5; más información divulgativa en Stephan Schlamminger, «Gravity measured with record precision,» Nature 560: 562-563 (29 Aug 2018), doi: 10.1038/d41586-018-06028-6. En este blog también puedes leer «La medida más precisa del valor de la constante de la gravitación universal», LCMF, 24 Ago 2010, y «Nueva medida de la constante de gravitación universal usando átomos fríos», LCMF, 18 Jun 2014.

En 1798 Henry Cavendish usó una balanza de torsión para determinar por primera vez el valor de la constante de gravitación universal. Desde entonces se han realizado gran número de mejoras en este tipo de balanzas, siendo la más relevante la sustitución de la pesa del péndulo por una placa delgada. Qing Li (Universidad Huazhong de Ciencia y Tecnologia, Wuhan, China) y sus colegas usan dos balanzas de torsión de este tipo que se diferencian en el método de medida: una mide el tiempo de oscilación (método TOS por Time-Of-Swing) y la otra mide la realimentación de la aceleración angular (método AAF por Angular-Acceleration-Feedback).

El método AAF suele ser más preciso que el método TOS, pero estos científicos chinos han logrado que ambos métodos tengan un error similar, de solo unas 11.6 partes por millón —el anterior récord, obtenido con AAF, tenía un error de 13.7 partes por millón. Por cierto, el valor más grande para la constante G (6.674 484 × 10−11) se ha obtenido por el método AAF, luego el más pequeño (6.674 184 × 10−11) con TOS.

¿Por qué difieren tanto los valores obtenidos con los métodos TOS y AAF? No se sabe cuál es la razón, pero hay dos explicaciones alternativas. La primera es la más obvia, que en alguno de los dos experimentos haya detalles técnicos que no se entienden con todo detalle y que provoquen que se subestimen los errores sistemáticos; por ejemplo, el comportamiento no lineal de la elasticidad de las fibras. La segunda es más especulativa, y mucho más sugerente, que exista nueva física que afecte de forma diferente a cada método de medida; esta opción es la que permite que este tipo de estudios se publiquen en revistas tan prestigiosas como Nature. Futuros estudios tendrán que clarificar cuál es la opción correcta.


Hay que diferenciar entre precisión y exactitud. En este caso debe hablarse de medidas más exactas (más cercanas al valor verdadero). En cuanto a su precisión, puede verse que hay unas mucho más precisas que otras (más o menos incertidumbre)
Cuidado, Rubén, se han obtenido las medidas más precisas (menor error en la medida), pues se ignora su exactitud (no conocemos el valor exacto, aún).
El articulo está bien redactado, han aumentado la precisión reduciendo el error a 11,6 partes por millón. Lo que no conocemos es la exactitud al carecer de un medio que nos dé el valor real, que por otro lado puede estar influenciado por otras variables que desconozcamos, sean del dispositivo de medida o de esa nueva física.
En los 80s era 6.672×10-11 N m2/kg2 según el libro de Resnik… Exijo la devolución de mi dinero!!!
En el mío 6.67 … Low precision 🙁
Tengo todavía una calculadora científica que fija el valor de G cómo 6,67259*10-11 N/m2/kg2.
Sería interesante un post sobre las diferencias y matices entre exactitud, precisión y error sistemático y aleatorio. Muchos lectures podrían apreciar entonces los datos y tablas de otra forma. No obstante, mi aporte:
1) Exactitud es una medida de la diferencia de un valor medido (estimado de datos experimentales) y del valor exacto. El problema es el valor exacto…Algunas teorías predicen estos valores y otras NO. Cuando no se tiene entonces una teoría sobre una cantidad, ¿qué se toma como exacto? En una medida directa de la magnitud correspondiente, se toma como «exacto» el valor medio de dicha cantidad de las medidas experimentales. Otro estimador, que cuentan en la escuela, es el valor absoluto de la diferencia del valor observado o medido con el valor exacto (o el valor medio)…O lo que es lo mismo, el denominado error absoluto o desviación de una medida con el valor exacto (o medio, usando el mejor estimador posible).
2) Precisión. Es algo mucho más sutil. La precisión es una medida esencialmente del tamaño de las barras de error de las medidas. Este tamaño está relacionado con el número de dígitos o cifras significativas que conocemos con precisión de una magnitud o cantidad dada.
3) Error. Es un concepto más versátil y engloba sutilmente a cada uno de los dos anteriores. El error sistemático es un error de calibración, y hace que las medidas, aún estando agrupadas, se desvían del valor verdadero, exacto o medio (caso de no tener medio teórico de estimación). El error aleatorio es un error de reproducibilidad relacionado con el instrumento usado, que hace que las medidas no salgan muy similares (no están agrupadas) o tienen barras de error grandes.
Y aquí ojo, porque se confunde o puede confundir la dispersión del error (dada por la varianza o la desviación estándar o típica) con el número de cifras significativas, pero también es un concepto diferente. Las medidas pueden estar «dispersas» y tener barra de error grande o pequeña, así que el tema es delicado. Porque creo que a veces cuando ponen el típico dibujo de la diana se confunde eso precisamente…Pues todos los blancos los ponen con cruces…Y eso no es la precisión…La precisión es el tamaño de de las ¡cruces o impactos! y no la dispersión, pero lo mismo yerro y hay alguien que lo entienda de otra forma…Dicho de otra forma, un cañón dispara de forma precisa si puede ajustar bien a un blanco de cierto tamaño con su bala, no si el blanco tiene impactos dispersos…Es muy fácil reproducir impactos con un cañon impreciso sobre una diana cercana, pero eso no es precisión…Precisión es reproducir exactamente los impactos de la misma forma…
Resumen:
1) Exactitud. Diferencia o distancia de las medidas al valor verdadero o medio. El valor exacto a veces no se puede conocer. Un bayesianista diría cosas muy raras sobre esto, jajajaja.
2) Precisión. Tamaño de las medidas o de las barras de error de las medidas. Por ejemplo, una calculadora de 10 dígitos es más precisa que una de 4 dígitos (supuesta bien calibrada, porque permite dar números con mayor precisión).
3) Error. El sistemático mide la exactitud, el aleatorio la dispersión de las medidas en torno a la media (no el tamaño de las barras de error, creo es algo interesante de destacar). En la escuela el error absoluto mide la exactitud y el error relativo o la varianza y desviación estadística se suelen «vender» como medidas de la precisión, pero creo hay sutiles diferencias.
Otro concepto relacionado es el del propio concepto de medida (directa o indirecta). Lo ideal es siempre medir una magnitud de forma directa, pero a veces uno tiene que conformarse con medidas indirectas que relacionan la magnitud a medir con otras. Eso lleva al concepto de propagación del error, relacionado con los conceptos previos. En una medida indirecta el error o desviación (de cualquiera de los tipos) puede deberse a errores de otros.
Para debatir también: los sistemas actuales de unidades como el SI cambian y se van haciendo más precisos con el tiempo. La importancia de G es generalmente minusvalorada…Fijaros que fijada la velocidad de la luz como 299792458 m/s y el valor de la constante de planck, hay dos formas diferentes de lograr una masa (quitando de momento la constante cosmológica del mapa): una es lo que han hecho para redefinir el kilogramo con c y la constante de Planck racionalizada (h entre dos veces pi), y la otra sería ¡mediante una precisa definición de G! Imaginaros que lográsemos una precisión del billón (europeo) en G, …También se me ocurre pensar en lo contrario, ya que hemos redefinido el kilogramo, me pregunto si no habría una forma alternativa de intentar mejorar la medida de G usando alguna otra técnica que no sea balanzas de torsión. Recordemos que G podría no ser fundamental de la misma forma que no lo es la constante de Fermi…
En relación con el último párrafo: https://francis.naukas.com/2014/06/18/nueva-medida-de-la-constante-de-gravitacion-universal-usando-atomos-frios/
Hola, Francis. ¿Los intervalos de confianza de las medidas son a 5 sigmas? ¿Y el de CODATA 2014? Si es así, ¿como puede haber sólo 2 sigmas de diferencia entre el valor de CODATA y el punto más alto de la gráfica correspondiente con una de las dos medidas? Parece una discrepancia a más de 5…
Amarashiki y Francis, muchas gracias por las explicaciones.
En el post se habla de valores únicos, todos ellos con los mismos decimales y comparando las 2 medidas nuevas contra la anterior, por lo que seguramente he interpretado mal el concepto por tontuna intrínseca supina y he pensado que la precisión era exactamente la misma y únicamente se refería a exactitud.
En definitiva, lo que se ha conseguido es disminuir la barra de error.
Por cierto Amarashiki (o quien sea), ya que lo mencionas ¿puedes ampliarme más la diferencia entre la barra de error y la dispersión? Cuanto más dispersión de datos mayor será la barra de error y menor la precisión.
Gracias y saludos.
Buena pregunta…Yo creo que eso no queda claro en los habituales dibujos de la diana…
La dispersión estadística es, al menos según entiendo yo, una medida de cuánto de agrupados están los valores en torno al valor medio o exacto, no es un tema de las barras de error, pero este concepto siempre me liaba a mí mucho en su día. Te lo diré de otra forma…Una pena no tener un dibujo aquí…Pero puede servir el gráfico de Francis de este artículo, ¿las medidas más precisas son las de menor barra de error o las que están más agrupadas o cercanas a la media, independientemente del tamaño de la barra de error? Es decir, ¿son más precisas las dos medidas de punto rojo o la tercera medida empezando por abajo a pesar de su tamaño de la barra de error porque su valor medio está más cerca del valor exacto? Nota una cosa:cada punto ahí es también el resultado de promediar y reducir otros muchos datos de otras medidas (el proceso de calibrado es esencial para determinar tu error experimental y el tamaño de tus barras de error,…Es decir, no solamente importa tengas una balanza de precisión o bien una regla muy precisa, sino como la usas y el método que usar para medir -eso está implícito en los comentarios de Francis a cerca de los dos métodos usados para obtener los 2 valores ultrapecisos de G)…
Porque puedes realizar un disparo preciso con una bala de cañón si está cerca, pero no lejos…si no apuntas…¿Dirías Rubén que hay mucha dispersión o poca en las medidas diferentes del diagrama de la medida de G? Lo normal, al final, es que los experimentalistas hacen converger los datos a un valor preciso con el avance de la técnica experimental…