
El caos determinista se asocia a ecuaciones sin solución exacta, a diferencia de los sistemas integrales. Sin embargo, si hay un algoritmo para calcular un objeto matemático, entonces existe una fórmula exacta (normalmente implícita) para describir dicho objeto. El diagrama de bifurcación de la aplicación logística (logistic map) es uno de los paradigmas del caos determinista. Existe una solución exacta «cerrada» general, aunque no está escrita usando funciones elementales y su evaluación requiere métodos numéricos; aún así, en ciertos casos particulares, también existen soluciones explícitas que se pueden escribir con funciones elementales. Por supuesto, esta expresión general implícita es inútil en la práctica, siendo siempre mucho más eficiente iterar la aplicación logística usando un ordenador.
Schröder en 1870 encontró la solución analítica para , dada por
, donde
; esta solución analítica ilustra la naturaleza del caos en la aplicación logística, el comportamiento cuasiperiódico, ya que la función
es periódica con un periodo irracional, en concreto,
. En lenguaje común se puede decir que el caos en aplicaciones como la logística es resultado de un comportamiento cuasiperiódico con periodo irracional. Maritz en 2020 se inpiró en la solución de Schröder para obtener la solución exacta para
, dada por
, donde
, y
es una función invertible con el siguiente desarrollo en serie
,
donde , y
,
para La solución se ha obtenido por el método de Frobenius (sustituir el desarrollo de potencias de la función y su inversa resolviendo las ecuaciones de recurrencia para sus coeficientes). Los interesados en los detalles disfrutarán del artículo de Milton F. Maritz, «A note on exact solutions of the logistic map,» Chaos 30: 033136 (20 Mar 2020), doi: https://doi.org/10.1063/1.5125097.
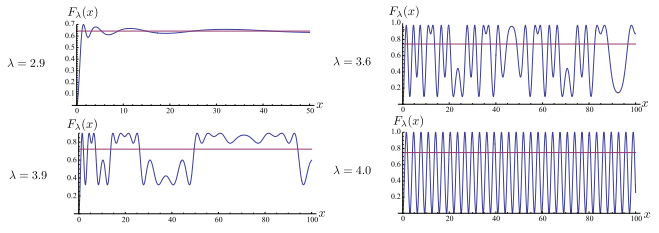
La evaluación numérica de la función es sencilla. En la figura se muestran cuatro ejemplos (nota que en el artículo original se escribe
).

Esta figura muestra la representación tridimensional de la función para
, y
.
Por supuesto, se han obtenido otras expresiones matemáticas para la solución exacta de la ecuación logística. Los aficionados al método de la matriz de transferencia (yo he publicado varios artículos científicos usando este método para metamateriales fractales) disfrutarán con S. Rabinovich, G. Berkolaiko, …, S. Havlin, «»Logistic map»: an analytical solution,» Physica A 218: 457-460 (1995), doi: https://doi.org/10.1016/0378-4371(95)00163-2 (más detalles en la tesis de maestría de Viviana Costinela Preduna, «The logistic map of matrices», Universitat Politècnica de València (2012), https://riunet.upv.es/handle/10251/27378). También se puede obtener la solución exacta usando el método de los determinantes (M. Bruschi, «Determinantal solution of the logistic map,» Journal of Physics A: Mathematical and General 31: L153 (1997), doi: https://doi.org/10.1088/0305-4470/31/7/003). Quienes prefieran usar el método de las funciones de Green para obtener una representación integral de la solución exacta leerán con agrado a Savely Rabinovich, Victor Malyutin, Shlomo Havlin, «An explicit solution for the logistic map,» Physica A 264: 222-225 (1999), doi: https://doi.org/10.1016/S0378-4371(98)00439-7.
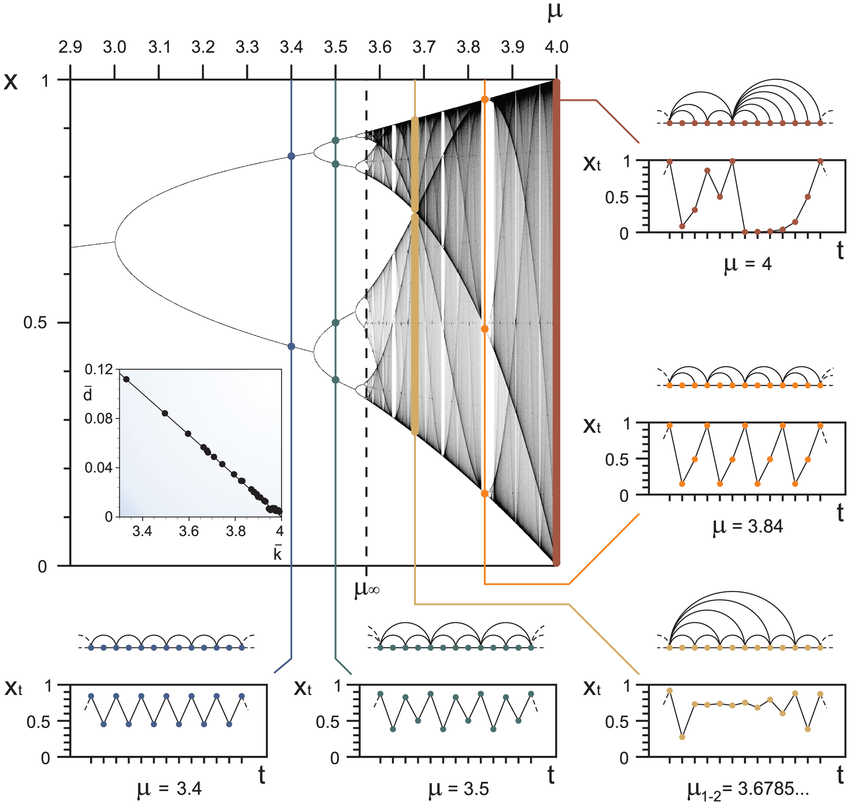
Los pocos despistados que aún ignoren qué es la aplicación logística y cuál es su diagrama de bifurcaciones quizás necesiten algunos comentarios adicionales. La aplicación logística es , con
, y
. Popularizada por el biólogo Robert May en 1975 como modelo discreto para poblaciones biológicas, pasó a la historia gracias al artículo «periodo tres implica caos» de Li y Yorke (1975), https://www.jstor.org/stable/2318254. Como es fácil comprobar, para
, resulta
, para
, luego la población inicial
se extingue; para
, resulta
, para
, con la población alcanzando de forma monótona este valor de equilibrio; sin embargo, para
, también obtenemos
, para
, pero con la población oscilando entre dos valores que de forma simultánea van convergiendo al valor de equilibrio.
Por encima de la aplicación no converge, oscilando entre varios valores de forma alternativa; para
, la población
oscila de forma alternativa entre dos posibles valores, es decir, en
ha ocurrido una bifurcación de periodo dos; en el punto
ocurren dos bifurcaciones de periodo dos, conduciendo a que la población
oscile de forma alternativa entre cuatro posibles; de manera sucesiva ocurren nuevas bifurcaciones de periodo dos hasta que para
aparece el caos, la población
va pasando por infinitos valores diferentes, una solución cuasiperiódica (como una solución que fuera periódica con periodo infinito). Más allá aparecen algunas regiones de periodo impar, como para
, con un periodo igua a tres. Este comportamiento de la aplicación logística es genérico para toda aplicación y siempre se cumpe que si hay soluciones de periodo tres, entonces hay regiones con comportamiento caótico (en rigor cuasiperiódico). Feigenbaum descubrió en 1979 que los cocientes de las diferencias entre los valores de
consecutivos a los que aparecen las bifurcaciones de periodo dos, cuatro, ocho, etc., tiende a un valor constante
, llamada constante de Feigenbaum, que es universal (independiente de la aplicación considerada). También existe una segunda constante de Feigenbaum, animo al lector a profundizar sobre ellas.
Esta pieza participa en la Edición 11.6: Conjeturas del Carnaval de Matemáticas, que en esta ocasión organiza Miguel Ángel Morales Medina en su famoso blog Gaussianos. Si te atreves a participar (el último día es el 29 de noviembre de 2020), debes comunicarlo en su blog, o con un tuit con etiqueta #CarnaMat11_6 (citando a @gaussianos y @CarnaMat). o mediante un email a gaussianos@gmail.com.
Como esta edición está dedicada a las conjeturas, me gustaría recordar que la conjetura de la universalidad de la constante de Feigenbaum fue demostrada usando ordenador (computer-assisted proof) por Oscar Lanford III, «A computer-assisted proof of the Feigenbaum conjectures,» Bulletin of the American Mathematical Society 6: 427-434 (1982), doi: https://doi.org/10.1090/S0273-0979-1982-15008-X (con ciertas correcciones por parte de Jean-Pierre Eckmann, Peter Wittwer, «A complete proof of the Feigenbaum conjectures,» Journal of Statistical Physics 46: 455-475 (1987), doi: https://doi.org/10.1007/BF01013368). No se logró la demostración sin ordenador hasta el trabajo de Mikhail Lyubich, «Feigenbaum-Coullet-Tresser universality and Milnor’s Hairiness Conjecture,» Annals of Mathematics 149: 319-420 (1999), doi: https://doi.org/10.2307/120968, arXiv:math/9903201 [math.DS] (01 Mar 1999).


Muchas gracias por la entrada, Francis.
Recomiendo a los lectores un maravilloso video divulgativo al respecto de la aplicación logística y el caos:
The Feigenbaum Constant (4.669) – Numberphile https://www.youtube.com/watch?v=ETrYE4MdoLQ
Un saludo.
Gracias, Ramiro, por recordar este vídeo de Brady Haran.
Hola Francis,
estaba leyendo esta entrada con interés y me encuentro con que has usado una gráfica nuestra sobre el estudio del mapa logístico a través de los grafos de visibilidad pero que ni mencionas ni citas el origen de esa gráfica.
Me permito poner las referencias aquí para aquellos lectores que puedan estar interesados (y a ti, darte un cariñoso tirón de orejas)
Saludos,
Lucas
https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0022411
Bartolo Luque, Lucas Lacasa, Fernando J. Ballesteros, Alberto Robledo
Feigenbaum graphs: a complex network perspective of chaos
PLoS ONE 6(9) (2011)
Bartolo Luque, Lucas Lacasa, Fernando J. Ballesteros, Alberto Robledo
Analytical properties of horizontal visibility graphs in the Feigenbaum scenario
Chaos 22, 013109 (2012)
Gracias. La costumbre en este blog es poner la referencia a cada figura en el nombre del archivo. En este caso: «https://francis.naukas.com/files/2020/11/PLoS-ONE-e22411-doi-10-1371-journal-pone-0022411-Feigenbaum-Graphs.png»