Los materiales microestructurados con una conductividad térmica ultrabaja me interesaron hace quince años. Hoy en día el foco está en los materiales nanoestructurados formados por capas (casi-)bidimensionales. Science publica un material con una conductividad térmica de 0.10 ± 0.02 W/(K m) a temperatura ambiente, o sea, solo cuatro veces mayor que la del aire; se trata de una superred (superlattice) de Bi₄O₄SeCl₂, formada por nanocapas alternas de BiOCl y Bi₂O₂Se. Se ha diseñado para suprimir la contribución de los fonones transversales y longitudinales responsables del límite de Cahill–Pohl para la conductividad mínima de un material. Las nuevas técnicas de fabricación de estos materiales prometen revolucionar el campo de los aislantes térmicos en la nanoescala.
Einstein publicó en 1911 el primer modelo teórico de la conductividad térmica en sólidos. Hoy usamos los fonones para entender el transporte del calor. Para reducir la conductividad térmica hay dos posibilidades. Por un lado, reducir la longitud de dispersión de los fonones (que depende de la interacción fonón-fonón y de la presencia de defectos), que tiene como límite inferior la mitad de la longitud de onda (por debajo de la cual ya no se puede usar el concepto de fonones). Y por otro lado, reducir la velocidad de grupo de los fonones (que requiere un control de su relación de dispersión); siendo una propiedad intrínseca del material que depende de su estructura y composición, solo se puede controlar con un diseño ex profeso del material. Las superredes y los materiales de van der Waals son el camino más prometedor para lograr nuevos récord en conductividad térmica ultrabaja. El nuevo récord es un buen ejemplo.
¿Para qué sirven estos materiales? A mí me interesan desde el punto de vista de la ciencia básica (termofísica fundamental), pero se ha propuesto su uso en dispositivos termoeléctricos para minimizar el calor residual y como barrera térmica eficiente para el recubrimiento de turbinas de gas. No sé si el costo actual de la fabricación de superredes bajará lo suficiente para que estas aplicaciones acaben siendo una realidad. El artículo es Quinn D. Gibson, Tianqi Zhao, …, Matthew J. Rosseinsky, «Low thermal conductivity in a modular inorganic material with bonding anisotropy and mismatch,» Science 373: 1017-1022 (27 Aug 2021), AOP (15 Jul 2021), doi: https://doi.org/10.1126/science.abh1619. Más información divulgativa en la nota de prensa de la Universidad de Liverpool, «Researchers discover a new inorganic material with lowest thermal conductivity ever reported,» Phys.org, 15 Jul 2021, y en Shi En Kim, David G. Cahill, «Pushing low thermal conductivity to the limit,» Science 373: 963-964 (27 Aug 2021), doi: https://doi.org/10.1126/science.abk1176.
Quizás no te interese, pero publiqué unos análisis perturbativos de la propagación de ondas térmicas en materiales unidimensionales con conductividad térmica ultrabaja: J. Pérez, F. R. Villatoro, …, P. Fernández de Córdoba, «Heat transfer between a gas and an ultralow thermal conductivity porous structure,» Applied Mathematics and Computation 204: 687-693 (2008), doi: https://doi.org/10.1016/j.amc.2008.07.008; F. R. Villatoro, J. Pérez, …, P. Fernández de Córdoba, «Perturbation analysis of the heat transfer in porous media with small thermal conductivity,» Journal of Mathematical Analysis and Applications 374: 57-70 (2011), doi: https://doi.org/10.1016/j.jmaa.2010.08.038.

Los fonones son las cuasipartículas (ondas que se comportan como partículas) asociadas a la vibraciones de la estructura cristalina de un material. Los fonones que se propagan en el material se pueden descomponer en fonones longitudinales (L o ⫽), asociados a la contracción y expansión en la dirección del movimiento, y fonones transversales (T o ⊥), asociados a vibraciones de cizalla en la dirección perpendicular al movimiento. En los cristales cuya celda unidad tiene más de un tipo de átomo se habla de fonones acústicos (A), cuando todos los átomos de la celda unidad vibran en la misma dirección, y fonones ópticos (O), cuando los átomos de la celda unidad vibran en direcciones opuestas. Así podemos hablar de fonones acústicos longitudinales (LA), acústicos transversales (TA), ópticos longitudinales (LO) y ópticos transversales (TO).
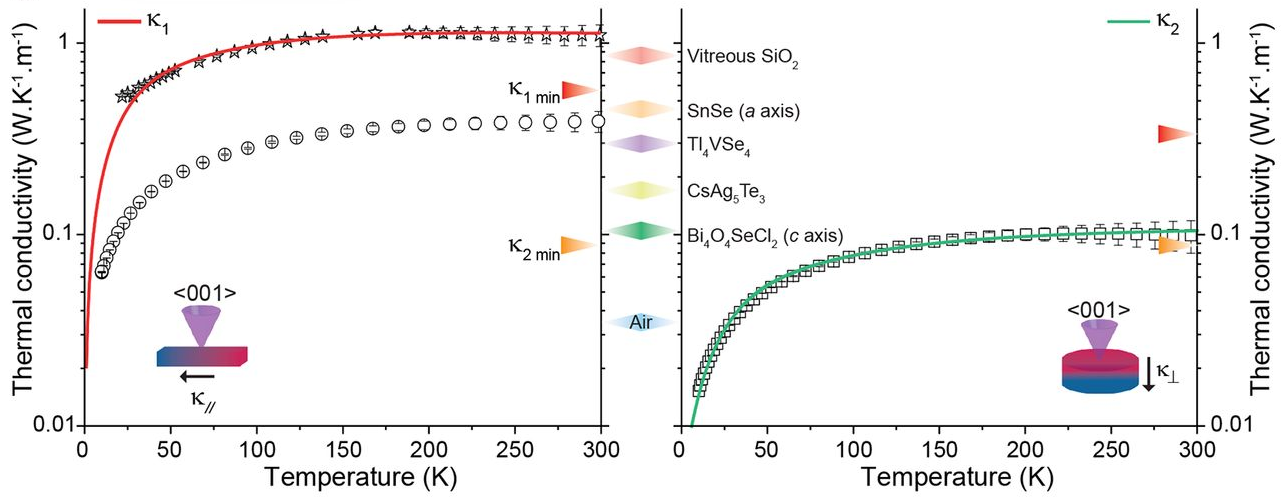
Para caracterizar los diferentes tipos de fonones se usa la llamada relación de dispersión (la figura ilustra algunos ejemplos). La función ω(k) representa la dependencia de la frecuencia (o energía) con el número de onda (o momento lineal). En el régimen de baja frecuencia (aproximación de Debye) se tiene ω = v k, donde v es la velocidad de fase; se define la velocidad de grupo como la derivada de la relación de dispersión, vg = dω/dk. Para un único fonón con una relación de dispersión general, la conductividad térmica κ1(T) se calcula con el modelo de Debye–Callaway; para temperatura ambiente se usa el límite asintótico para alta temperatura, que conduce a una conductividad térmica mínima κ1min (llamado límite de Cahill–Pohl). El diseño de un material con conductividad ultrabaja tiene por objeto modificar la relación de dispersión para reducir el valor mínimo κ1min. Para un material multicapa (como una superred formada por dos materiales alternados) se usa un modelo modificado, κ2(T), que tiene en cuenta fonones LA y LO, y que presenta un valor mínimo diferente κ2min. Para los interesados en los detalles, la información suplementaria del artículo detalla todas las fórmulas matemáticas de ambos modelos.

En una superred de (Bi₂O₂)ₘXₙ se combinan capas catiónicas de (Bi₂O₂)²⁺ con capas aniónicas X que resultan en un conductividad térmica anisótropa (y anarmónica). En la dirección cristalográfica (001) se ha medido una conductividad térmica del BiOCl muy baja, 0.15 ± 0.02 W/(K m) a temperatura ambiente, por debajo del valor límite de Cahill–Pohl (κ1min); aunque por encima de κ2min = 0.125 W/(K m). Por otro lado, en el Bi₂O₂Se se ha medido una conductividad de 1.0 ± 0.2 W/(K m) a temperatura ambiente, aunque en este caso dicho valor está por encima de κ1min.

La idea del nuevo artículo es aprovechar la anisotropía (anarmonicidad) que aparece la relación de dispersión en una superred formada por nanocapas alternas de un BiOCl y Bi₂O₂, para reducir la contribución de los fonones acústicos transversales (TA) y longitudinales (LA). El nuevo material, Bi₄O₄SeCl₂, tiene una conductividad térmica medida en el plano de un monocristal de 1.0 ± 0.1 W/(K m) a temperatura ambiente, que está por encima de κ1min = 0.6 W/(K m). La medida en la dirección paralela al plano cristalino de la superred es muy baja, 0.4 ± 0.1 W/(K m), algo menor que κ1min (véase la figura que abre esta pieza). Pero en la dirección en la dirección perpendicular plano cristalino de la superred la conductividad térmica es de solo 0.10 ± 0.02 W/(K m), valor que hay que comparar con la del aire 0.026 W/(K m). Este valor ultrabajo (véase la figura que abre esta pieza) está por debajo de κ1min, pero muy próximo a κ2min, luego se puede explicar con el modelo teórico κ2(T).
En resumen, los récords son siempre noticia, aunque este blog solo divulgo algunos de ellos, mostrando mi sesgo de interés. En este caso, mi sesgo parte de que estudié los avances en materiales con conductividad ultrabaja hace quince años, porque pretendía publicar unos análisis perturbativos de la propagación del calor en medios microestructurados unidimensionales y quería «vender» que eran útiles, más allá de su interés matemático. La propagación del calor en el nuevo material nanoestructurado publicado en Science se describe muy bien con dichos modelos. Por ello ha llamado mi atención. Si te interesa el tema, te recomiendo consultar los artículos que cito.


Miguel, el equipo chino ha repetido de forma independiente el logro del grupo de Martinis para Google en 2019, pues usa el mismo algoritmo (diseñado por el grupo de Martinis). La diferencia es que en lugar de usar 53 cúbits y 20 ciclos en un ordenador Sycamore de 54 cúbits (un cúbit falló), usan 56 cúbits y 20 ciclos en un ordenador Zuchongzhi de 66 cúbits (dicen que todos funcionan, pero solo usan 56 para «optimizar» el algoritmo de Martinis, no me queda claro lo que significa).
Repetir un hito siempre es necesario; pero en la historia de la computación cuántica solo permanecerá el logro del grupo de Martinis, como los primeros en lograrlo.
El artículo es Yulin Wu, Wan-Su Bao, …, Jian-Wei Pan, «Strong quantum computational advantage using a superconducting quantum processor,» arXiv:2106.14734 [quant-ph] (28 Jun 2021); si saco tiempo escribo una pieza en el blog, ahora mismo no tengo tiempo ni para un borrador.
Se me ocurre una aplicación algo diferente, a modo de prueba y menor escala, como recubrimiento de termopares de alta temperatura. Se podría quizá afinar más tanto la repuesta a los cambios de temperatura como la eliminación de ruido de la señal para determinada mediciones.
Rai, el problema es cómo el sensor en el interior de la burbuja tiene contacto con el exterior de la burbuja en equilibrio térmico. La métrica de Alcubierre no lo permite.