[youtube=http://www.youtube.com/watch?v=YCA0VIExVhg&w=580&h=580]
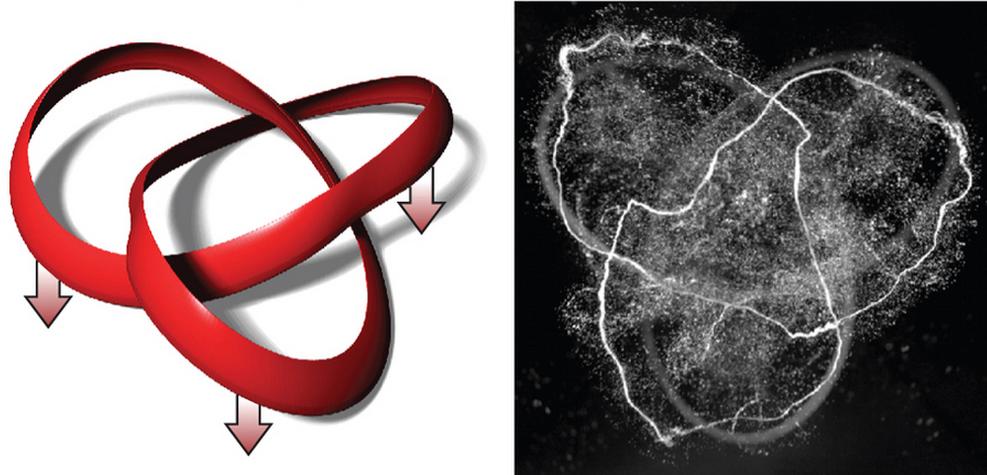
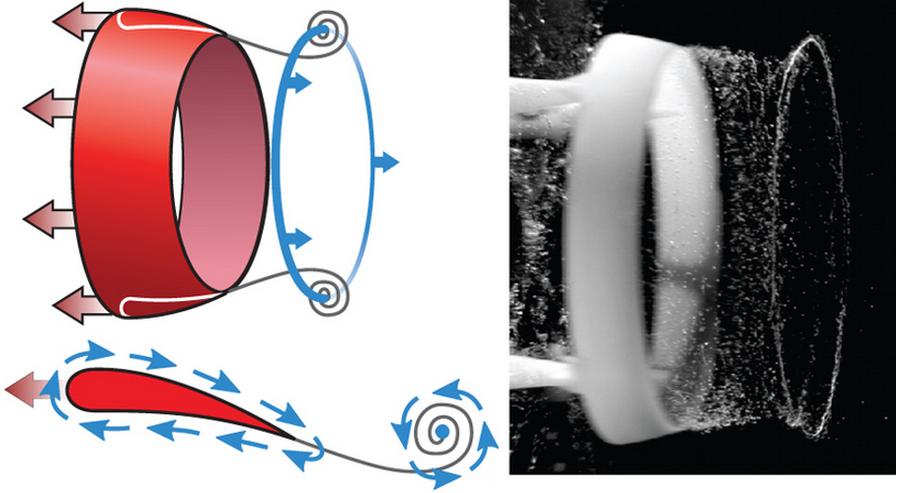
Una afición de algunos fumadores es hacer vórtices de humo en forma de anillo (o circunferencia). La manera más sencilla es forzar que el fluido pase por un agujero circular. También se pueden producir estos vórtices acelerando de forma brusca un «ala» con forma circular. Lo más sorprendente es que si el «ala» tiene forma de nudo de tres hojas, el resultado es un vórtice con forma de nudo de tres hojas, como muestra este vídeo. Para fabricar estas «alas» en forma de nudo, Dustin Kleckner y William T. M. Irvine de la Universidad de Chicago han usado una impresora 3D. El resultado es realmente alucinante, vórtices de agua «anudada» realmente hipnóticos. El artículo técnico es Dustin Kleckner, William T. M. Irvine, «Creation and dynamics of knotted vortices,» Nature Physics, AOP 03 Mar 2013.
Las «alas» con forma de nudo de tres hojas han sido realizadas con plástico y con diferentes tamaños. Se acoplan a un sistema que les imprime un movimiento brusco, con lo que se forma el vórtice en el fluido con una geometría y topología análoga a la del «ala.» Este tipo de vórtices fueron predichos a finales del s. XIX, aunque hasta ahora no se habían podido producir en laboratorio (según los autores del artículo técnico ellos son los primeros en lograrlo).
Los vórtices son resultados del teorema de Kelvin de la circulación. La circulación alrededor de una curva cerrada que envuelve al «ala» es cero en reposo, pero cuando el «ala» se pone en movimiento se produce la fuga hacia atrás de un vórtice de circulación igual pero girando en sentido contrario para compensar dicho movimiento. En un «ala» en forma anular, el vórtice forma un toroide (anillo). Según la teoría y como han demostrado los experimentos, si el «ala» tiene forma de nudo de tres hojas, el vórtice adquiere dicha forma. El movimiento de este «ala» cruza el vórtice, pero la robustez del movimiento del fluido hace que el vórtice sobreviva y nos brinda todo un espectáculo. Los que tengan gafas 3D de dos colores pueden disfrutar con el siguiente vídeo.
[youtube=http://www.youtube.com/watch?v=rcnw8NeJqjU&w=580&h=580]
.



Aqui esta el teorema http://www.icmat.es/press/papers/2012/23
Puede ayudarme por favor de como ver una aplicacion de una ecuacion de esta forma: es de fluidos creo que en mi ignorancia asociados con HOJAS DE VORTICES,
u_t(x,t)=v u_xx(x,t)+(uHu)_x(x,t)
u: flujo,
v: viscosidad,
Hu: Transformada de Hilbert
Le agradezco cualquier colaboracion de antemano
Juan, se trata de la ecuación de Constantin-Lax-Majda (Communications on Pure and Applied Mathematics 38: 715–724 (1985), doi: 10.1002/cpa.3160380605). Busca en Google Scholar los artículos que lo citan (cientos) y encontrarás muchas aplicaciones en las que esta ecuación unidimensional se puede usar bajo ciertas hipótesis.