Antonio Acín (ICFO/ICREA, Barcelona, España) y varios colegas responden a esta pregunta en un artículo en Nature Communications que presenta un protocolo cuántico para amplificar la aleatoriedad de los eventos naturales que sean aleatorios para hacerlos completamente aleatorios. El artículo no demuestra que estos eventos existan en la Naturaleza, pero introduce la siguiente dicotomía: o bien nuestro universo es completamente determinista, o bien existen eventos naturales que son totalmente aleatorios. Todo el mundo sabe que la física clásica es totalmente determinista (aunque el caos determinista limita su predictibilidad) y que la física cuántica permite lo aleatorio, aunque ello no implica la existencia de cualquier forma de aleatoriedad en la Naturaleza. El problema de distinguir entre (pseudo)aleatoriedad y aleatoriedad completa puede parecer de interés sólo para los filósofos, pero también es importante desde un punto de vista práctico, pues los bits aleatorios son útiles en muchas aplicaciones (protocolos criptográficos, juegos de azar o simulación numérica de sistemas físicos y biológicos). El artículo técnico es Rodrigo Gallego et al., «Full randomness from arbitrarily deterministic events,» Nature Communications 4: 2654, 30 Oct 2013 (arXiv:1210.6514 [quant-ph]).
En física clásica cualquier aleatoriedad observada un sistema es manifestación de nuestra descripción imperfecta de dicho sistema. En física cuántica todas las predicciones de los resultados de los experimentos se describen en términos probabilísticos (esto llevó a que físicos como Albert Einstein pensaran que es una descripción incompleta de la realidad). Sin embargo, los teoremas de no-go de John Bell implican que las teorías de variables ocultas (que explican la cuántica aludiendo a un mundo subcuántico clásico) son incompatibles con las predicciones de la mecánica cuántica. En concreto, todas las teorías de variables ocultas compatibles con una estructura causal local predicen correlaciones entre los eventos separados un intervalo de tipo espacio que satisfacen las llamadas desigualdades de Bell, pero estas desigualdades son violadas por algunas correlaciones entre partículas cuánticas. Estas correlaciones tienen su origen en la no-localidad de la física cuántica.
Las razones son sutiles, pero la no-localidad cuántica no implica necesariamente la existencia de procesos totalmente impredecibles en la Naturaleza. Por un lado, certificar un proceso como impredecible requiere usar el principio de no-señalización (la comunicación instantánea de información no es posible). Y por otro lado, las verificaciones experimentales de las desigualdades de Bell requieren que el observador realice ajustes o elecciones al azar en los aparatos de medida, pero certificar estas acciones como aleatorias es imposible (es imposible garantizar que los procesos mentales detrás de estas decisiones sean aleatorios).
Por todo ello, la existencia de procesos completamente al azar debe ser estudiada en detalle. El nuevo artículo propone un protocolo cuántico de amplificación de la aleatoriedad. Se parte de una fuente de bits pseudoaleatorios y tras la aplicación del protocolo se obtiene una nueva fuente de bits aleatorios perfectos, sin ninguna correlación con todos los acontecimientos que estén fuera de su cono de luz, es decir, que pueden haber sido una causa potencial.
Se parte de una fuente S de bits pseudoaleatorios, cada uno con una probabilidad P(x|e), siendo e cualquier evento que sea causa del bit x. Se cumplirá que ε ≤ P(x|e) ≤ 1-ε, donde 0 < ε ≤ 1/2. Los bits son deterministas si ε = 0 y completamente aleatorios si ε = 1/2.El objetivo del nuevo protocolo de amplificación de la aleatoriedad es construir una nueva fuente S(ε) de bits aleatorios con un valor ε que tienda hacia 1/2. Santha y Vazirani (1984) demostraron que la amplificación de la aleatoriedad es imposible sólo con el uso de los recursos clásicos. Colbeck y Renner (2012) construyeron un protocolo de amplificación de aleatoriedad que logra que ε→1/2, pero partiendo de una fuente S de bits muy aleatorios, con 0,442 < ε ≤ 0,5. El nuevo protocolo supera este inconveniente.
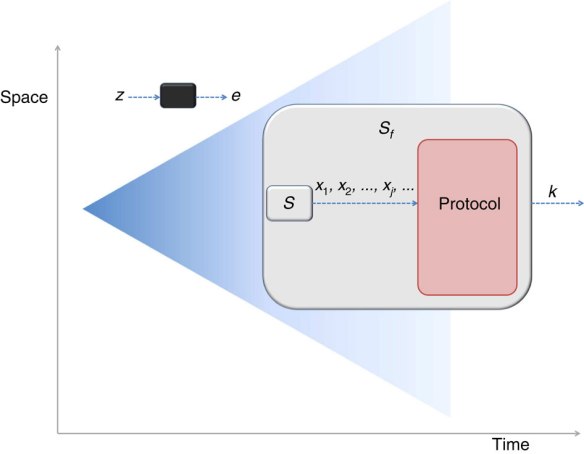
No pretendo explicar los detalles del nuevo protocolo de amplificación de la aleatoriedad, sólo presentar la idea de su funcionamiento (mostrado en la figura de arriba). En el primer paso un conjunto de observadores elige al azar, usando la fuente pseudoaleatoria S, los ajustes de su experimento y realiza una medida cuántica. Los observadores se agrupan en quintetos y para cada quinteto se realiza un test de Mermin-Bell para chequear la no localidad; se descartan los quintetos que no superen este test. El resto de los quintetos se agrupa en bloques del mismo tamaño Nd, llamados bloques de destilación. El siguiente paso se repite cuantas veces sea necesario. Se elige uno de los bloques de destilación utilizando la fuente S pseudoaleatoria; se comprueba si cumple la desigualdad de violación máxima de la no localidad del test de Mermin-Bell; en caso contrario, se descarta y se repite el proceso de elegir un nuevo bloque de destilación (si aún queda alguno, en cuyo defecto se repite todo desde el principio). El paso final es elegir un bit entre los primeros tres bits de cada quinteto en el bloque de destilación seleccionado; para ello se utiliza un algoritmo de votación por mayoría. El resultado es un bit de una fuente aleatoria con ε→1/2 (conforme N y Nd crecen). Los interesados en más detalles pueden consultar el artículo técnico (que incluye las demostraciones de los dos teoremas en sendos apéndices).