La teoría de cuerdas es un marco físico-matemático que ofrece herramientas para desarrollar modelos teóricos de sistemas físicos. Generaliza la teoría cuántica de campos, por lo que permite extender sus modelos teóricos en varias direcciones. Su ventaja es que añade ciertas propiedades deseables a dichos modelos, lo que permite resolver ciertos problemas graves. Se suele destacar que permite incorporar la teoría general de la relatividad evitando las divergencias ultravioletas que aparecen en la teoría cuántica de campos. Gracias a ello abre un camino firme hacia una futura teoría cuántica de la gravedad.
Sin embargo, para un físico teórico, lo más interesante de la teoría de cuerdas es la amplia red de dualidades que ofrece. Modelos teóricos muy diferentes entre sí, en apariencia, están conectados por diccionarios derivados de estas dualidades. No se trata de simples analogías físicas. La conexión es profunda y permite ciertos milagros matemáticos. Algunos cálculos teóricos que rayan lo imposible en un modelo se vuelven asequibles en su modelo dual. Por supuesto, la teoría de cuerdas aún está en desarrollo y hay muchas herramientas que intuimos pero aún tenemos que desarrollar.
El gurú de la teoría de cuerdas, Edward Witten, cree que la teoría de cuerdas, igual que el cálculo de diagramas de Feynman, debería ser una herramienta que todo físico teórico debería conocer. Nos lo cuenta en Edward Witten, «What every physicist should know about string theory,» Physics Today 68: 38-43 (Nov 2015), doi: 10.1063/PT.3.2980. Permíteme un resumen breve de su artículo (sin fórmulas matemáticas) para motivar su lectura.
La búsqueda de una teoría cuántica de la gravedad en 4D (un espaciotiempo 3+1) usando las herramientas de la teoría cuántica de campos presenta ciertos problemas sin solución. Para ilustrarlos, Witten nos propone usar dichas herramientas para buscar una teoría cuántica de la gravedad en 1D (un espaciotiempo 0+1). Más sencillo imposible. La geometría del espaciotiempo será una curva abierta o una curva cerrada, en ambos casos parametrizada por el tiempo propio.
La interacción gravitacional se describe en la teoría clásica de la relatividad general en 4D mediante una acción que depende de la constante de Newton (G), el determinante del tensor métrico (g), el escalar de curvatura (R) y la constante cosmológica (Λ). En 1D se puede usar la misma acción, aunque el escalar de curvatura es idénticamente nulo (una curva no tiene curvatura intrínseca, aunque tenga curvatura extrínseca si se sumerge en un espacio tridimensional). Por tanto, la acción clásica de Einstein se reduce al término que depende de la constante cosmológica. Más sencillo imposible.
Por supuesto, a la acción de Einstein en el vacío hay que añadirle campos de materia que actúen como fuentes de la gravitación. Witten nos propone añadir D campos clásicos escalares (X). El término Λ se puede reemplazar por m²/2, actuando como la masa de dichos campos escalares. A partir de la acción de Einstein, con un gauge adecuado, se obtiene como ecuación para la función de onda Ψ(X) de los D campos escalares las ecuaciones (clásicas) relativistas de Klein–Gordon en D dimensiones. El resultado parece pura magia matemática.
Witten nos propone ver las cosas al revés. En lugar de D campos escalares en un espaciotiempo 1D, nos propone interpretar el resultado como se hace en teoría de cuerdas, como un campo escalar en un espaciotiempo de D dimensiones. Repito. Una teoría cuántica de la gravedad en una dimensión describe una partícula escalar (de espín cero) con masa (m) que se propaga en un espaciotiempo (inducido) con D dimensiones. En general, la métrica de dicho espaciotiempo inducido se puede seleccionar de forma arbitraria. Luego puede ser un espaciotiempo de Minkowski (plano con métrica lorentziana), lo habitual, pero también cualquier espaciotiempo M curvo en D dimensiones con métrica (G) euclídea, lorentziana o con cualquier otra signatura. La asombrosa generalidad de la teoría de cuerdas en acción.
La versión cuántica de la teoría clásica que Witten nos propone se obtiene aplicando integrales de camino. Se integra la métrica en 1D módulo difeomorfismos. Por supuesto, en 1D sólo hay un invariante, la longitud de la curva (espaciotiempo en 1D); en realidad la duración T (edad del universo), pues la curva está parametrizada por el tiempo propio. La integral de camino requiere considerar todas las posibles trayectorias X(t) que empiezan en el punto X(0)=x en t = 0 y acaban en el punto X(T)=y en t=T. Como es obvio el formalismo de integrales de Feynman en este caso es equivalente a la primera cuantización de la teoría. Pero, recuerda, estamos estudiando una teoría de gravedad cuántica, luego también hay que integrar respecto a todas las métricas g(t), módulo difeomorfismos (reparametrizaciones del tiempo en 1D). El resultado es equivalente a la segunda cuantización de la teoría.
Sorprendente. La cuantización mediante integrales de camino de nuestra teoría de gravedad en 1D con D campos escalares resulta en una teoría cuántica de campos para un campo escalar en un espaciotiempo de D dimensiones. Además nuestra gravedad cuántica de juguete permite describir múltiples partículas escalares en interacción mutua. Basta elegir un potencial de autointeracción adecuado; nuestra teoría nos deja la libertad de elegir el modelo físico que deseemos estudiar. Así se puede aplicar el formalismo de diagramas de Feynman para estudiar dichas interacciones. En la figura de arriba se muestra un diagrama de Feynman para una interacción cúbica (los vértices tienen tres partículas).
¿Cuál es el problema de la teoría que hemos desarrollado? Que las interacciones son puntuales (porque la gravedad cuántica de la que partimos está descrita en una espaciotiempo de 0+1 dimensiones). Por tanto, aparecen divergencias ultravioletas (un problema similar al de los divisores en la mecánica celeste de Poincaré para el problema de los tres cuerpos). Hay que imponer condiciones físico-matemáticas adicionales para seleccionar las teorías en las que se puedan realizar con éxito todos los cálculos. En teoría cuántica de campos la opción más natural es exigir que el modelo de la autointeracción conduzca a una teoría renormalizable. En general nuestra gravedad cuántica tiene un gran poder predictivo y describe un gran paisaje (landscape) de modelos teóricos (como le ocurre a la teoría de cuerdas).
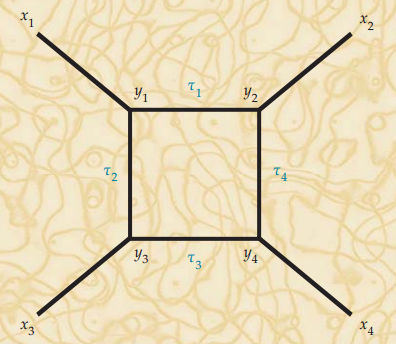
El origen de las divergencias ultravioletas en nuestra teoría cuántica de la gravedad en 1D son las interacciones puntuales. La solución más natural a este problema es incrementar la dimensión del espaciotiempo en el que se construye la gravedad cuántica. Por supuesto, ese es el camino seleccionado en la teoría de cuerdas. En un espaciotiempo en 2D con métrica lorentziana 1+1 podemos recorrer el mismo camino. Dicho espaciotimepo Σ se llama hoja del mundo (worldsheet) y su métrica está descrita por una matriz de 2×2. A diferencia del caso 1D, las métricas 2D no son localmente equivalentes bajo difeomorfismos. Pero dicha invariancia reduce las cuatro componentes a solo dos componentes independientes y resulta que el escalar de curvatura (R) no es nulo pero es invariante.
La generalización de la acción Einstein a 2D es sencilla y muestra una propiedad muy sugerente. La acción es invariante bajo transformaciones de Weyl (reescalados de la métrica g → λ g). Esta propiedad sólo se cumple en 2D y cuando se omite el término de constante cosmológica. Bajo esta condición toda métrica en Σ es localmente trivial (equivalente a un espaciotiempo plano), como ocurría en 1D. El worldsheet es una superficie (2D) de Riemann caracterizada (módulo difeomorfismos) por una serie de parámetros complejos (en lugar de números reales). En los diagramas de Feynman las líneas se sustituyen por tubos (cilindros) y los vértices en lugar de puntos se transforman en bifurcaciones entre tubos (como ilustra la figura de arriba). Gracias a ello se evitan todas las divergencias ultravioletas (todos los posibles ceros en los divisores en el desarrollo de perturbaciones para las interacciones).
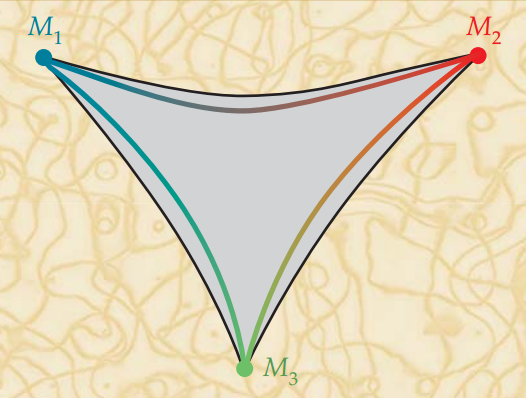
La diferencia más importante entre la gravedad cuántica en 1D y en 2D es la correspondencia entre estados y operadores. En la primera, hay una clara diferencia entre ambos. Pero en la segunda, tenemos una teoría de campos conformes en la que estados y operados son equivalentes entre sí. Un estado (el punto p rojo marcado en el doble toro Σ de la izquierda) donde se aplica cierto operador es equivale (vía la invariancia Weyl) a la aparición de un tubo cuerdístico (en el doble toro la derecha) que representa tanto el estado como el operador.
La gravedad cuántica en 2D que hemos descrito corresponde a una teoría de cuerdas (definidas como las secciones transversales a los tubos en el worldsheet). La gran ventaja de los tubos es que su curvatura intrínseca es cero, lo que está detrás de que la teoría de campos conforme en el worldsheet sea integrable. Esto significa que podemos describir el comportamiento de las cuerdas mediante ecuaciones de onda lineales y que podamos escribir la solución general a dichas ecuaciones; se suele usar un desarrollo de Fourier y el resultado depende de las condiciones de contorno para los extremos de la cuerda, sean periódicas (cuerda cerrada), de Dirichlet (cuerda con extremo fijo en una brana), o de Neumann (cuerda con extremo libre).
Witten nos destaca un punto importante que no debemos olvidar. Las fórmulas cuerdísticas generalizan las fórmulas en las teorías de campos. Básicamente se sustituye el tiempo propio (τ) que es una variable real en el espaciotiempo 0+1, por una variable compleja espaciotemporal (σ,τ) en el espaciotiempo 1+1. Esto elimina todas las divergencias ultravioletas posibles, toda singularidad en un vértice se sustituye por una superficie suave localmente plana y en la que no hay ningún tipo de singularidad. Pero, repito, todo lo que se puede hacer en teoría de campos se generaliza sin divergencias en teoría de cuerdas. Por ello esta última es la extensión natural de la primera. No es algo exótico o forzado. Lo natural es generalizar las teorías de campos como teorías de cuerdas, sabiendo que tras realizar los correspondientes cálculos sin divergencias, el resultado se podrá devolver al formalismo original y podrá ser comparado con los resultados experimentales (si fuera necesario).
Por supuesto, toda teoría cuántica de la gravedad es una teoría cuántica del espaciotiempo. ¿Cómo emerge el espaciotiempo en teoría de cuerdas? El espaciotiempo inducido M con su métrica G(X) dependiente de los campos con masa X está codificado en los datos que definen la teoría conforme de campos en 2D definida en el worldsheet Σ con métrica g. La interpretación semiclásica de esta construcción es la aparición simultánea de un espaciotiempo y de un conjunto de campos masivos que describen partículas que se propagan en dicho espaciotiempo.
En general, la teoría de cuerdas no especifica de forma única ni el espaciotiempo inducido, ni el conjunto de campos cuánticos que contiene. En pie de igualdad con la mecánica de Newton que describe las trayectorias de las partículas en función de las fuerzas aplicadas, pero que no especifica de forma única las fuerzas que se pueden dar en la Naturaleza. Witten compara la situación con la emergencia de la mecánica clásica a partir de la mecánica cuántica. El universo es cuántico, aunque en ciertos límites parezca clásico. De igual forma, el espaciotiempo clásico y los campos cuánticos emergen a partir de la teoría de cuerdas. El universo es cuerdístico, aunque en ciertos límites parezca descrito por campos cuánticos en un espaciotiempo clásico.
Por supuesto, el propio Witten confiesa que la respuesta cuerdística a la naturaleza cuántica del espaciotiempo no es ni completa, ni del todo satisfactoria. El espaciotiempo clásico emerge de algo más profundo, pero Witten se excusa, todavía no conocemos en detalle lo que es. Cita a los trabajos sobre el universo holográfico, entre otros a Maldacena, y nos deja con ese sinsabor tan típico de los artículos sobre teoría de cuerdas. Aún no conocemos la versión final de la teoría. Por ello hay preguntas que no sabemos responder. Sin embargo, la teoría de cuerdas es la extensión natural de las teorías de campos que describen nuestro universo y debería formar parte de los conocimientos imprescindibles para todo físico teórico.
En resumen, espero haberte animado a leer el artículo de Witten, que incluye algunas fórmulas matemáticas y algunos razonamientos que he omitido. Por supuesto, te he contado mi interpretación de dicho artículo, que puede estar alejada de lo que el propio Witten tiene en mente. Pero espero que ello te anime a leer su artículo. Si eres físico, seguro que lo disfrutarás.



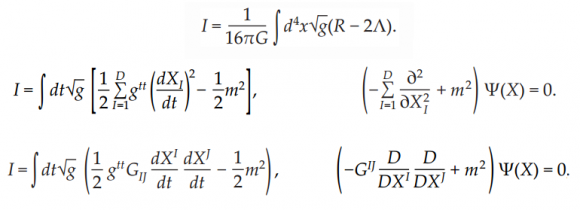


Antonio, las teorías conformes 2D son integrables, luego son teorías no perturbativas que no requieren ninguna renormalización. Esta integrabilidad es la clave de la teoría de cuerdas. En 2D no es necesario aplicar teoría de perturbaciones.
Estoy bastante agradecido estoy con su fantástico trabajo en esta entrada.
Hoy mismo me leo el paper de Witten. Gracias por la motivación
Para enriquecer un poco la entrada, también vale la pena leer (si alguien está interesado en algo mas asequible) este ensayo de Polchinski:
String theory to the rescue: http://arxiv.org/abs/1512.02477
Enfatiza que la teoría de cuerdas es un marco conceptual aún falta de princpios físicos guía, entre líneas hay comentarios profundos como una especulación sobre si el principio holográfico podría ser la idea física de fondo.
Muuuy bueno. Muchas gracias.
A mí sí que me ha animado. No me lo pierdo.
Creo que lo más importante del artículo es que se explica claramente algo fundamental: la teoría de cuerdas no es una «invención» de Físicos y Matemáticos «chiflados» a los que les gusta jugar a inventar nuevas dimensiones y nuevos objetos exóticos sin conexión con la realidad:la teoría de cuerdas es una GENERALIZACIÓN NATURAL de la teoría cuántica de campos. Esta generalización es totalmente natural porque los objetos estrictamente puntuales no pueden existir en la naturaleza, un objeto de dimensión 0, radio 0, longitud 0 es algo sin significado Físico. Además, al dibujar los diagramas de Feynman de las interacciones entre partículas puntuales se producen discontinuidades insalvables (la recta no toca al rectángulo en ningún punto), sin embargo, si consideramos objetos con una mínima extensión ¡las rectas se transforman en cilindros que se unen de forma continua formando superficies de Riemann y las discontinuidades desaparecen! ¿Quien puede pensar que esto es un juego Matemático sin sentido?
Uno de los descubrimientos más sorprendentes de los últimos años es que nuestro Universo se comporta de forma «dual», sistemas que aparentemente son completamente diferentes son en realidad totalmente equivalentes: un sistema cuántico con simetría conforme sin gravedad en 3D es equivalente a un espacio-tiempo 4D con gravedad, distancias muy pequeñas son equivalentes a distancias muy grandes, sistemas con energías muy grandes son «duales» a sistemas con energías muy pequeñas… por si fuera poco la complementariedad de los agujeros negros nos indica que 2 observadores ven cosas totalmente diferentes en el borde de un AN: un observador lejano observa que la masa del AN disminuye (por radiación Hawking) hasta que finalmente el AN explota sin embargo un observador justo borde el AN no observa la radiacion Hawking, el siempre mide la misma masa M del AN. Ambos observadores no se pondrán de acuerdo ni en la métrica, ni en la energía ni en los tamaños que miden ¡ Ambos ven Universos distintos ! ¿Como es esto posible? Sorprendentemente esto podría resolverse usando la simetría conforme: https://arxiv.org/abs/1511.04427
En mi opinión las dualidades, la indeterminación cuántica, los espacios internos de las partículas, las amplitudes complejas, etc apuntan claramente a la existencia de nuevas dimensiones pequeñas «enrrolladas» (o sea periódicas) tal y como predice la teoría de cuerdas. El descubrimiento de nuevas dimensiones y de la verdadera naturaleza del espacio-tiempo es el reto más trascendente y más revolucionario al que se ha enfrentado nunca la Física. El espacio-tiempo probablemente surge de la interacción entre entidades fundamentales (cuerdas, branas y quizás alguna cosa más aún por descubrir) y la Física teórica nos está descubriendo un Universo mucho más extraño e increíble de lo que nadie hubiese nunca imaginado. Los agujeros negros parecen tener la clave del misterio del espacio-tiempo: la inmensa cantidad de grados de libertad que poseen, la aparente no-localidad, los wormholes, el entrelazamiento, etc son fenómenos que la nueva Física moderna está comenzando a explicar con el inmenso poder de las Matemáticas. Una de las cosas más sorprendentes es que a pesar de la ignorancia de la mayor parte de la humanidad un pequeño grupo de seres humanos pueden adentrarse dentro de los agujeros negros, viajar al instante 0 de la creación del Universo, simular con absoluta precisión la forma de las ondulaciones del espacio-tiempo…. Con las Matemáticas realmente unos pocos seres humanos parecen tener el poder de los «dioses» ¿Puede existir algo más increíble y fascinante que esto?
la verdad no entendí nada pero como dijo sócrates la verdadera saviduría está en reconocer la propia ignorancia