Los modelos cosmológicos que explican el universo sin materia oscura y sin energía oscura copan titulares. El astrofísico suizo André Maeder, a sus 75 años, logra su minuto de gloria tras rescatar del olvido un modelo cosmológico invariante de escala que propuso en 1978. A la vejez, viruelas; tras tres manuscritos en arXiv, ni corto ni perezoso, ha colado tres artículos en The Astrophysical Journal (ApJ). La televisión pública suiza le ha entrevistado [fuente] y muchos medios se han hecho eco de su trabajo. Su modelo contradice las observaciones cosmológicas actuales, por ello ningún cosmólogo se molestará en refutarlo; ni siquiera merece la pena (not even wrong).
Weyl (1918–1921) introdujo una teoría de la gravitación invariante de escala para unificar el electromagnetismo y la gravitación. Dirac (1973) la rescató para unificar la interacción fuerte y la gravitación. Bouvier y Maeder (1977), y Maeder (1978) propusieron un modelo cosmológico invariante de escala. Incompatible con las observaciones a principios de los 1980, el modelo fue olvidado. Hoy sigue igual, pero un artículo en ApJ cuyo título finaliza con la pregunta «¿la caída de la materia oscura?» (The Fall of Dark Matter?) es irresistible para los medios (y muchos legos).
Permíteme opinar, no te sulfures en los comentarios. No tengo nada contra el autor, ni contra los medios que lo han glorificado. Solo te voy a contar mi opinión como físico y divulgador; recuerda que no soy cosmólogo (Maeder tampoco lo es), ni tampoco astrofísico (Maeder lo es). En cualquier caso si prefieres estudiar el nuevo modelo por tu cuenta te recomiendo empezar por estos tres manuscritos en arXiv de 2016: Andre Maeder, «Scale invariant cosmology I: the vacuum and the cosmological constant,» arXiv:1605.06315 [gr-qc]; «Scale invariant cosmology II: model equations and properties,» arXiv:1605.06316 [gr-qc]; «Scale invariant cosmology III: dynamical models and comparisons with observations,» arXiv:1605.06314 [gr-qc].
Por supuesto, quizás prefieres omitir los manuscritos en arXiv y recurrir a los artículos publicados en ApJ, una revista con revisión por pares; en dicho caso disfrutarás con Andre Maeder, «An Alternative to the ΛCDM Model: the Case of Scale Invariance,» The Astrophysical Journal 834: 194 (13 Jan 2017), doi: 10.3847/1538-4357/834/2/194, arXiv:1701.03964 [astro-ph.CO]; «Scale-invariant Cosmology and CMB Temperatures as a Function of Redshifts,» The Astrophysical Journal 847: 65 (21 Sep 2017), doi: 10.3847/1538-4357/aa88cf, arXiv:1708.08648 [astro-ph.CO]; «Dynamical Effects of the Scale Invariance of the Empty Space: The Fall of Dark Matter?» The Astrophysical Journal 849: 158 (10 Nov 2017), doi: 10.3847/1538-4357/aa92cc, arXiv:1710.11425 [astro-ph.GA].
Quizás, incluso, eres de los que siempre recurre a las fuentes originales; tranquilo, no me remontaré a Weyl (1918), o a Dirac (1973), no te abrumes: P. Bouvier, A. Maeder, «Consistency of Weyl’s geometry as a framework for gravitation,» Astrophysics and Space Science 54: 497–508 (1978), doi: 10.1007/BF00639452; A. Maeder, «Metrical connection in space-time, Newton’s and Hubble’s laws,» Astronomy and Astrophysics 65: 337-343 (1978), [SAO/NASA ADS]; A. Maeder, P. Bouvier, «Scale invariance, metrical connection and the motions of astronomical bodies,» Astronomy and Astrophysics 73: 82-89 (1979), [SAO/NASA ADS].
[PS 26 Nov 2017] Recomiendo la lectura de Sabine Hossenfelder, @skdh, «Astrophysicist discovers yet another way to screw yourself over when modifying Einstein’s theory,» Backreaction, 26 Nov 2017. «Maeder’s papers contain a lot of fits to data but no consistent theory. [The] math is wrong. [Please] stop hyping this paper.» [/PS]
[PS 04 Dic 2017] También recomiendo leer a Ryan F. Mandelbaum, «Dark Matter Is Not Dead,» Gizmodo, 28 Nov 2017. [/PS]
La teoría de la gravitación de Einstein se basa en el principio de equivalencia y cumple el principio de covariancia general, pero no es invariante de escala. Weyl construyó una teoría de la gravitación invariante de escala (la primera aparición del término gauge en la física), que no cumple el principio de equivalencia, pero cumple lo que Dirac bautizó como principio de co-covariancia general (en lugar de vectores usa covectores y en lugar de tensores usa cotensores). Bouvier y Maeder construyeron un modelo cosmológico (isótropo y homogéneo) basado en la teoría de Weyl, inspirados por Dirac; el modelo se basa en usar la métrica cosmológica de Friedmann–Lemaître–Robertson–Walker (FLRW) insertada en las ecuaciones de la gravitación de Weyl con un factor de escala que solo depende del tiempo, siguiendo a Dirac; gracias a ello la métrica resultante cumple el principio de equivalencia, aunque sigue siendo co-covariante (en terminología de Dirac).
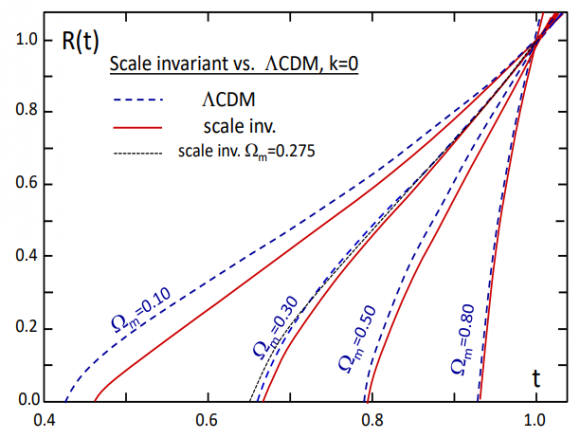
Para el espaciotiempo vacío, la invariancia de escala del modelo cosmológico de Maeder conduce a la aparición de una constante cosmológica dependiente del tiempo, Λ(t) = 3/(λ(t) c t), donde λ(t) es el parámetro de escala, c es la velocidad de luz en el vacío y t es el tiempo en el modelo FLRW. Casi parece obvio, la constante cosmológica es resultado de la densidad de energía del espaciotiempo vacío. El parámetro de escala λ(t) se ajusta para que ahora sea λ = 1 y que el valor actual de la constante cosmológica sea el estimado por Planck 2015. Un cálculo sencillo conduce a que hace 13 800 millones de años (edad del universo según las estimaciones astrofísicas de la edad de las estrellas más viejas, dice Maeder) el valor de λ(t) era de λ ~ 1,5; por tanto, el valor de la escala cósmica (gauge cósmico) varía muy poco (entre 1 y 1,5), por lo que su efecto en épocas recientes (para z < 10) en el modelo FLRW es muy pequeño. Así que todas las observaciones cosmológicas (para z < 10) son compatibles con la nueva cosmología invariante de escala. Mejor, imposible, … para Maeder.
¿Pero qué pasa para z=1100 cuando aparece la radiación cósmica de fondo? Maeder no menciona la cuestión en ningún artículo, y parece que los revisores de ApJ hacen la vista gorda. Obviamente, su teoría describe un universo dominado por la energía oscura, en total desacuerdo con las teorías cosmológicas actuales. Como bien sabes la energía oscura es un fenómeno reciente (significativo para z < 2). Un universo temprano (z→∞) dominado por la energía oscura requiere la reescritura de todos los libros de texto sobre cosmología y sobre física de partículas, pues en los grandes colisionadores de partículas exploramos el estado del universo cuando tenía un nanosegundo tras el big bang. Todo bajo la alfombra; ya se sabe que quien no quiere ver…
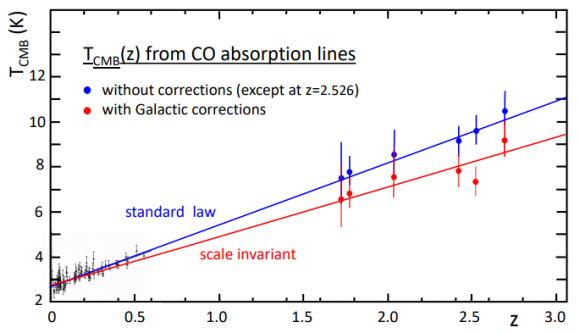
¿Cómo explica el fondo cósmico de microondas (CMB) la cosmología de Maeder? Se aplica el modelo FLRW a un universo que contiene materia y radiación (cada una con su ecuación de estado estándar), y tras un cálculo sencillo se encuentra una relación entre la temperatura de la radiación T(t) y el parámetro de escala, T²(t) R²(t) λ(t) = constante, donde R(t) es el radio del universo. El resultado para z<3 es muy parecido al del modelo ΛCDM; para valores grandes de z la divergencia es dolorosa, pero Maeder omite hacer ningún comentario al respecto y evita que aparezca pista alguna en sus figuras (quizás para que los revisores de ApJ puedan volver a hacer la vista gorda sin ningún remordimiento).
¿Qué es la materia oscura a escala cósmica? La cosmología invariante de escala de Maeder modifica la ley de Newton con un término de origen cosmológico, cuyo valor depende del tiempo; este término solo es relevante a escala cósmica (cúmulos y supercúmulos galácticos). La aplicación del teorema del virial a las galaxias que se mueven en un cúmulo galáctico conduce a una modificación de su masa efectiva (M), que resulta ser mayor que la masa virial o visible (Mv), la asociada a las propias galaxias según su luminosidad. El cociente depende del tiempo, luego la cantidad de materia oscura cambia para los cúmulos más viejos. Maeder pone dos ejemplos, el cúmulo de Coma para el que M/Mv ~ 4,2–12,3 y el cúmulo Abell 2029 para el que M/Mv ~4,7–17,2; estos valores explican el porqué dichos cúmulos parecen tener más masa que la visible (M>Mv). Entre líneas Maeder sugiere que eso ocurre para todos los cúmulos, aunque las observaciones afirmen lo contrario.
Pero qué pasa para escalas más allá de la de los supercúmulos. Pues Maeder hace mutis por el foro y omite cualquier mención al asunto. Como el fondo cósmico de microondas es ficticio, no existe como tal, las medidas a dicha escala tampoco tienen sentido, luego no hay que explicar lo que no existe. ¿Por qué los revisores de ApJ no se han cuestionado lo que predice la teoría a esta escala? Yo lo hubiera hecho, pero no he sido revisor.
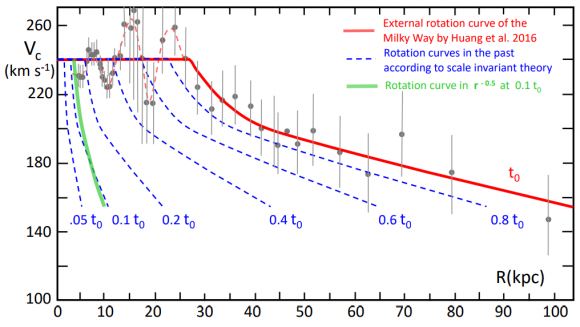
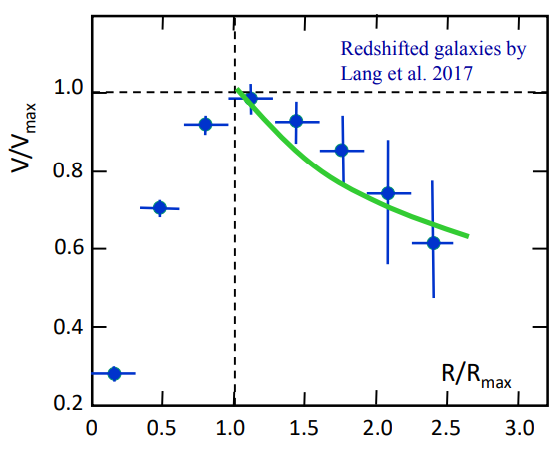
¿Cómo explica la cosmología de Maeder las curvas de rotación galáctica? No hagas hipótesis a priori, la cosmología de Maeder no predice una aceleración mínima constante tipo MOND o Verlinde que explique que la velocidad de rotación del gas en el halo galáctico sea prácticamente constante. Dicho comportamiento de las curvas de rotación galáctica no tiene una explicación sencilla en la teoría de Maeder. Por tanto, según Maeder, dicha observación tiene que ser incorrecta. Tras citar un artículo de la mismísima Vera Rubin afirma sin rubor que, en realidad, la velocidad parece constante solo donde hay materia visible (bariónica), pero cuando te alejas deja de ser constante, aunque decae más lentamente que lo que predice la teoría de Newton (debido al pequeño efecto de la corrección de su ley predicha por la cosmología invariante de escala). Por tanto, la materia oscura no existe a escala galáctica, pero las teorías tipo MOND o Verlinde también están equivocadas a dicha escala. Maeder es así, si no casa algo, se lo hace casar.
¿Cuál es el estado actual de la gravitación de Weyl (o invariante de escala) para un físico teórico? El problema de las anomalías en esta teoría descarta dicha teoría como una opción razonable en la búsqueda de una teoría cuántica de la gravedad. Por cierto, Maeder afirma en todos sus artículos que los problemas cuánticos de estas teorías no son relevantes en su modelo cosmológico, que solo requiere la validez de la teoría a nivel clásico. ¿Cuál es el estado de la gravitación de Weyl para un cosmólogo? Un modelo que ajusta el presente, pero es incapaz de ajustar el pasado es inútil para un cosmólogo; estos científicos siempre están preocupados por el pasado del universo y el presente les importa un comino (eso sí, para ellos el presente es z < 10 y el pasado es z → ∞).
¿Cuál es el estado de la cosmología de Maeder para un divulgador científico o para un periodista científico? La última maravilla entre las maravillas; ningún editor rechazará un artículo que afirma que la materia oscura y la energía oscura no existen, que son consecuencia del espaciotiempo vacío (el objeto más fácil de entender para un lego de toda la física). Máxime cuando se trata de un astrofísico suizo de prestigio que sigue activo tras su jubilación (envidia me da, ya me gustaría a mí tener la mente tan fresca como para publicar artículos en ApJ con esa edad). La tercera edad no es óbice para revolucionar la cosmología, ¡quién se resiste a una noticia así!
En resumen, la cosmología invariante de escala de Maeder no convencerá ni a los cosmólogos a favor del modelo ΛCDM de consenso, ni a los cosmólogos en contra de todo consenso. Una teoría que la semana que viene será olvidada por todo el mundo quizás no merezca más atención. Yo no hubiera escrito esta entrada si no me lo hubiera pedido mi amigo César Tomé.
Lo confieso, he disfrutado leyendo los artículos de Maeder, no voy a mentir, sobre todo porque son muy fáciles de entender para un físico con un conocimiento básico de cosmología. Pero, no te equivoques, los avances más relevantes en cosmología están publicados en artículos muy difíciles de entender para un físico que no sea cosmólogo, porque para entender lo realmente relevante hoy en día no basta con haber estudiado las teorías de hace 100 años, o haber leído los libros de texto más recientes sobre cosmología.




Editorial de Nature. De hace dos semanas.
https://www.nature.com/news/dark-matter-hunt-fails-to-find-the-elusive-particles-1.22970
Jose, en este blog ya hablé de dichos resultados cuando se publicaron en arXiv (Xenon1T en mayo 2017 y PandaX-II en julio 2016). La noticia ahora es que aparecen en PRL.
Donde pone «la tercera edad no es ápice» igual querías poner óbice.
Yo no soy físico, ya me gustaría serlo, pero donde no hay mata no hay patata pero echo de menos alguna explicación para legos de lo de la invarianza de escala.
Yo tenía entendido que algo era invariante de escala cuando conservaba alguna propiedad al varia la escala, entonces veo que alguien plantea esto para el espacio vacío y pienso «ah, pero es que las propiedades del espacio o de la gravedad o lo que sea cambian con la escala???»
Una explicación sin vacas esféricas, por favor, yo pensaba que la gravedad era la misma sin importar la distancia o el tamaño.
La gravitación de Einstein es covariante general ds’=ds, para un cambio general de coordenados las longitudes locales (infinitesimales) se conservan (si cambias la escala, o las unidades de medida, cambian las distancias que mides). En la gravitación de Weyl invariante de escala, o co-covariante general, ds’=λ(x)ds, es decir, las longitudes locales pueden sufrir un escalado (si cambias la escala, o las unidades de medida, de forma adecuada no cambian las distancias que mides). En la cosmología invariante de escala se asume un universo homogéneo e isótropo, luego ds’=λ(t)ds; como resultado la expansión acelerada del espaciotiempo es aparente, resultado de un cambio de escala en la medida de distancias.
Recuerda que ds=g_μν dx^μ dx^ν, por lo que ds’=λ(t)ds implica g’_μν=λ²(t) g_μν, lo implica la aparición en las ecuaciones de Einstein de nuevos términos que dependen de λ(t) y sus derivadas, que resultan ser del tipo Λ_M g_μν, con Λ_M=Λ λ²(t), siendo Λ la constante cosmológica.
Muchas gracias por la explicación, Francis.
El cálculo convencional de la expresión de la aceleración del factor de escala en el modelo LambdaCDM de consenso puede consultarse en:
http://forum.lawebdefisica.com/entries/623-El-inicio-de-la-expansi%C3%B3n-acelerada-del-Universo-la-aceleraci%C3%B3n-del-factor-de-escala
Saludos.
Me sorprende (un poco) lo de Astrophysical Journal, pero como afirma Francis, hasta en las mejores familias se da: las publicaciones siempre están a la caza de un titular y en este caso, la propuesta y la circunstancia de Maeder es irresistible. No es la primera ni será la última.
Me recuerda el caso del estadounidense Garrett Lisi que en 2008 propuso una «teoría de todo» basada en un modelo 8-dimensional llamado E8, que tiene unas gráficas simétricas hermosas y simplemente irresistibles. Al final, como muchas otras propuestas, resultó que proponía más problemas de los que resolvía, pero esto no fue impedimento para que en ese entonces Lisi se convirtiera en rockstar y diera una plática TED que se hizo viral.
https://www.ted.com/talks/garrett_lisi_on_his_theory_of_everything
El ácido Peter Woit ha hablado mucho de este fenómeno en su blog «Not Even Wrong» aunque su ira normalmente la dirige a la Teoría de Cuerdas.
http://www.math.columbia.edu/~woit/wordpress/
Excelente post, como siempre por parte de Francis. Saludos!
Al final del sexto párrafo dice:
[..,] gracias a ello la métrica resultante cumple el principio de equivalencia, aunque sigue siendo co-covariante (en terminología de Dirac).
Creo que debería ser:
[..,] gracias a ello la métrica resultante NO cumple el principio de equivalencia, aunque sigue siendo co-covariante (en terminología de Dirac).
Muchas gracias por el post, Francis.
«Su modelo contradice las observaciones cosmológicas actuales». Como profano absoluto, me quedo con esto.
Supongo que a los profanos, al público en general, nos resulta profundamente insatisfactorio un universo en el que el 95% es materia oscura o energía oscura. Quizá el adjetivo «oscuro» sea el culpable, ¿no habría otro? Por eso nos interesamos por «modelos» que pretenden explicar sin oscuridad… pero las observaciones son las que mandan. Sólo queda esperar a que se avance en el conocimiento y den resultados los experimentos con la materia oscura…
Se llama oscura porque no interactúa con el espectro electromagnético, es decir, con la luz.
No hay otra razón. A mi me parece muy adecuado el término. Qué luego la gente se haga pajas mentales es problema de la gente que no ha mirado ni de qué se trata antes de hablar.
Es el problema de las revistas científicas, que siguen siendo revistas y buscan el titular fácil.
La falta de formación en estadística o matemáticas hace que les cuelen goles utilizando estadísticos inadecuados. Porque lo del anonimato de los autores en la mayor parte es discutible, si el autor es famoso se acepta enseguida, pese a que supuestamente la peer review se realiza de forma anónima.
Si contradice las observaciones no pasa de ser un bonito ejercicio.
Mm, el universo no aplica nada, ten en cuenta que nuestras fórmulas son la interpretación de lo que ocurre en el universo, no la realidad en sí.
Francisco me gustaría saber si tú crees que la materia y la energía oscura existen.
Antonio, en nuestro Universo, existen la materia oscura y la energía oscura. No se puede opinar al respecto, se trata de un hecho. Otra cosa diferente es que no conocemos su naturaleza; puedes opinar sobre lo que son, pero no sobre su existencia.
Sin evidencia científica directa no se puede afirmar que existan. Siendo que sus efectos pueden ser explicados modificando las leyes existentes. Simplemente no estamos seguros de su existencia o no existencia.
Roberto, la evidencia científica de su existencia es indiscutible. Que baste modificar las leyes de la física para explicar sus efectos no implica que no existan, todo lo contrario; si no existen no hay que modificar nada. Toda modificación de las leyes requiere la existencia de un motivo.
Antes de escribir aclaro que si creo en el fenómeno (porque ya se ha demostrado una anomalía gravitacional en las Curvas de Rotación de las Galaxias (CRG), rotan mas rápido de lo que deberían rotar) pero no creo en que exista una Materia Oscura para resolver esa anomalía, al menos para las galaxias. «la evidencia científica de su existencia es indiscutible», no estoy de acuerdo en la ciencia nada es indiscutible, todo esta abierto al cambio. «Que baste modificar las leyes de la física para explicar sus efectos no implica que no existan, todo lo contrario», si podría implicar que no existan, precisamente porque la aparente existencia de la Materia Oscura es una falacia provocada por la falta de la modificación de las leyes de la física, precisamente esa es la otra alternativa (al paradigma de la Materia Oscura) que daría solución a la anomalía gravitacional, las Ecuaciones de Campo de Einstein de la Teoría de la Relatividad General (TGR), son correctas hasta donde se ha confirmado, pero no da los los resultados correctos para las CRG, porque se necesita una teoría de la gravedad mas general que de los resultados correctos, como en su momento se necesito una teoría de la gravedad mas general (la TGR) que la Ley de la Gravitación Universal de Newton (LGU) para que diera los resultados correctos a las observaciones. «si no existen no hay que modificar nada», al contrario, si no existen hay que buscar por que la TGR a través de la LGU (la LGU es una aproximación de la TGR y se aplica a las CRG por que tienen un campo muy débil) no da los resultados correctos para las CRG (debido a la falacia de una materia no bariónica que aparentemente existe), la única alternativa siguiendo este camino es desarrollar una teoría mas general que la TGR. «Toda modificación de las leyes requiere la existencia de un motivo.» el motivo es resolver la anomalía gravitacional que existe en las CRG, las cuales rotan mas rápido de lo que deberían rotar con la materia bariónica que contienen y que no hay nada mas que esa materia y con eso se tiene que resolver el problema. Para concluir aclaro, el paradigma de la Materia Oscura responde a muchos mas problemas aparte de las CRG, pero siguiendo el principio de la Navaja de Ockam, se puede empezar con las galaxias, que me parece es uno de los caso mas sencillos para estudiar. Estoy trabajando en una nueva teoría (basa en primeros principios) para resolver el problema de las CRG utilizando la TGR y la LGU, solo con materia bariónica sin necesidad de Materia Oscura y estoy obteniendo muy buenos resultados en los ajustes. Yo creo en una Teoría Hibrida para resolver los dos principales problemas de universo, Materia Oscura y Energía Oscura, formada por una nueva teoría de la gravedad y nuevas partículas no bariónicas, Pero no creo en que, o todo sea Materia Oscura o todo sea una Nueva Teoría de la Gravedad, debemos trabajar en conjunto.