[PS 25 Abr 2018] Soñar es gratis. Esta entrada pretendía ser un sueño, pero ha sido malinterpretada por muchos lectores. Por ello, siguiendo los consejos vertidos en varios comentarios, la reescribo, a mi pesar. Ya no será un sueño. Lo siento por los aficionados a soñar. [/PS]
El modelo estándar de la física de partículas permite las corrientes neutras con cambio de sabor (FCNC) a nivel de lazo, pero las prohíbe a nivel de árbol; por tanto, las transiciones entre quarks de diferente sabor, pero con la misma carga eléctrica, como la de un quark bottom a un quark down (b → d), están muy suprimidas (son muy raras). El detector LHCb del LHC en el CERN ha observado a 3,4 sigmas un exceso en una desintegración b → d que implica la observación de una FCNC. En concreto, se han observado 38 ± 12 desintegraciones B0s → K∗0 µ+ µ−, con K∗0(892). Aún no se ha calculado la predicción teórica del modelo estándar para esta desintegración a nivel de lazo; quizás dicho cálculo explique toda la señal observada. O quizás no lo haga, y podamos soñar con que aparezca un exceso que requiera una contribución FCNC más allá del modelo estándar; en dicho caso, se trataría del primer indicio firme de la existencia de nuevas partículas aún no descubiertas.
Se han analizado 1,0 /fb de colisiones a 7 TeV c.m., 2,0 /fb a 8 TeV c.m., y 1,6 /fb a 13 TeV c.m, resultando una tasa de desintegración observada BR (B0s → K∗0 µ+ µ−) = [ 2,9 ± 1,0 (estad) ± 0,2 (sist) ± 0,3 (norm)] × 10−8. Por desgracia, no se ha publicado aún ninguna estimación teórica de alta precisión (al menos tan precisa como la observada) para la predicción del modelo estándar para esta desintegración; el artículo de LHCb sugiere una estimación a ojo de buen cubero, BR ≈ |Vtd/Vts| = O(10−8). Por ello, el sueño asociado a la interpretación como nueva física de los indicios del exceso a 3,4 sigmas, deben ser tomados como mucha precaución, como todo sueño. Eso sí, habrá que estar al tanto de la predicción con QCD en el retículo (LQCD) para esta desintegración que se debería publicar en los próximos meses. Quizás se explique toda la señal observada sin recurrir a la existencia de una FCNC a nivel de árbol.
Mientras tanto, podemos soñar que estamos viviendo una de esas épocas apasionantes en la historia de la física de partículas en la que empiezan a aparecer múltiples indicios de nueva física más allá del modelo estándar. Recuerda, soñar es gratis. El artículo es LHCb collaboration, «Evidence for the decay B0s → K∗0 µ+ µ−, » LHCb-PAPER-2018-004, arXiv:1804.07167 [hep-ex].
[PS 23 Abr 2018] He cambiado el título del original «LHCb observa a 3,4 sigmas una desintegración más allá del modelo estándar» al más comedido «LHCb observa a 3,4 sigmas una desintegración aún no calculada con el modelo estándar» por petición popular (confieso que el original era sensacionalista). En rigor, aún no sabemos si la observación se explica con el modelo estándar o si se trata de un exceso sobre la predicción del modelo estándar. De hecho, se estima que la predicción del modelo estándar a nivel de lazo será de BR (B0s → K∗0 µ+ µ−) ≈ 10−8, con lo que tiene el mismo orden de magnitud que la señal observada. [/PS]
Me han pedido una nueva explicación de lo que significan las sigmas de confianza estadística. La idea es contrastar una hipótesis, por ejemplo, que el exceso observado tiene su origen en una perniciosa fluctuación estadística en las colisiones analizadas. La validez de esta hipótesis (llamada hipótesis nula) se contrasta usando las propias observaciones asumiendo que existe un fondo de colisiones (sin el exceso) predicho (mediante el modelo estándar). Simplificando mucho, el exceso sobre el fondo se puede aproximar por una distribución normal (gaussiana) resultando un valor μ ± σ, donde μ es el valor medio del exceso y σ es la desviación típica (en el exceso de LHCb el exceso de 38 ± 12 desintegraciones). Según la hipótesis nula no debería existir el exceso, luego el exceso tiene μ/σ sigmas (en el exceso de LHCb unas 38/12 = 3,2 sigmas) de confianza estadística. Como ilustra la figura, tres sigmas implica que hay un 0,25% de posibilidades de que sea una fluctuación estadística y cinco sigmas de que haya un 0,00005% de que lo sea.
Por supuesto, el párrafo anterior es una simplificación extrema de un capítulo sobre contraste de hipótesis en un libro de texto de estadística. Más aún, hay libros de texto dedicados solo al contraste de hipótesis, incluso solo al contraste de hipótesis en física de partículas. El exceso observado por LHCb tiene 3,4 sigmas en lugar de 3,2 sigmas tras realizar un contraste de hipótesis riguroso; en dicho análisis se tienen en cuenta muchos efectos, como que el fondo no es plano, o como que el exceso no se distribuye según una distribución normal, presentando asimetrías, curtosis, etc.
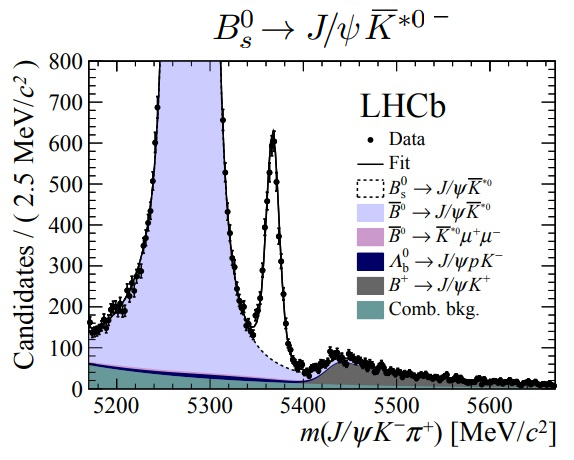
Un punto que me gustaría destacar es la diferencia entre exceso local y exceso global, el llamado efecto LEE (look-elsewhere effect); un exceso a ciertas sigmas en la región de energía entre [5200, 5600] GeV tiene muchas menos sigmas si se estudia en la región [5000, 6000] GeV, pues al ser dicha región 10/4 veces más grande se incrementa en un factor similar la probabilidad de encontrar fluctuaciones estadísticas grandes. Elegir de forma adecuada la región a estudiar para evitar el LEE (que, en rigor, es un sesgo cognitivo de confirmación) es un factor muy relevante en un análisis estadístico riguroso. En el análisis de LHCb se ha usado la misma región que en la desintegración B0s → J/ψ K∗0− (desintegración ilustrada en esta figura); no tengo conocimientos suficientes para valorar si dicha decisión está libre de sesgos y si un análisis más riguroso habría exigido considerar una región más amplia (con lo que la confianza estadística en la observación se reduciría por debajo de las tres sigmas).
En resumen, espero que esta breve discusión del concepto de sigmas como medida de la confianza estadística en contra de una hipótesis (que el exceso sea una simple fluctuación estadística) satisfaga a quienes me pidieron una explicación. Los interesados en más información pueden consultar, por ejemplo, el breve (48 pp.) Luca Lista, «Practical Statistics for Particle Physicists,» arXiv:1609.04150 [physics.data-an], o su libro (172 pp.) Luca Lista, «Statistical Methods for Data Analysis in Particle Physics,» Springer (2016), doi: 10.1007/978-3-319-20176-4.




vaya revuelo si se confirma!
Si no ando equivocado, ésto apuntaría a SUSSY? Daría crédito a la hipótesis de neutralinos como WIMPs? o está ya descartado por limites de exclusión?
Espaidual, se trata de una cuestión de opiniones, pero no apoya al neutralino, per se, quizás a un bosón Z prima (nueva U(1) o nueva SU(2), pero no necesita SUSY).
¡El que espera desespera…!
Que ha cambiado respecto de hace tres años?
https://francis.naukas.com/2015/03/19/nuevo-rumor-sobre-la-anomalia-b%E2%86%92k%CE%BC%CE%BC-en-lhcb/
Roger, ahora se ha observado un exceso en la desintegración tras analizar 4,6 /fb de datos, mientras que en 2015 solo se observó una anomalía en ciertos parámetros técnicos tras analizar 1,0 /fb de datos. Estos parámetros están asociados a los ángulos de los productos de la desintegración y su relación con ella es indirecta; ahora se ha realizado una observación directa. Por tanto, el resultado ahora es más firme que antes.
Vale, muchas gracias 😀
Tal vez valdría la pena enfatizar que esta noticia va sobre una transición b -> d, como el propio Francis señala en el texto, mientras que las anomalías «famosas» (las enlazadas en el comentario) se dan en transiciones b -> s. En principio podría no haber relación entre unas y otras.
Francis, lo primero agradecerte por tu blog. Pienso que tareas de divulgación como la tuya son indispensables para la ciencia.
Pero cuidado con esta entrada porque tu interpretación del resultado de LHCb no es correcta. El exceso es sobre la hipótesis de que no haya señal y el resultado de LHCb es totalmente compatible con lo esperado por el Modelo Estandar.
De todas formas el que LHCb haya sido capaz de medir este canal de desintegración (tremendamente suprimido) es muy relevante porque abre la veda para esclarecer si las anomalías observadas en b->s también están presentes en otras transiciones aún más suprimidas en el Modelo Estándar. De momento, es ahora trabajo de los teoricos mejorar la predicción del Modelo Estándar para esclarecer si hay o no nueva física en estas transiciones.
Gracias, Javi.
Hola Francis,
Te recomiendo que leas bien el articulo que citas. En el abstract encuentras estas frases:
A yield of 38±12 B0s -> K* mu+mu- decays is obtained, providing the first evidence for this decay with a significance of 3.4 standard deviations above the background-only hypothesis. The resulting branching fraction is determined to be B ( B0s → K∗μ+μ−) = [2.9±1.0 (stat)±0.2 (syst)±
0.3 (norm)]×10−8. While no SM prediction of the branching fraction of this decay exists in the literature, the measurement is consistent with a naıve scaling of B(B0→K∗0μ+μ−) by a SM-like
value of |Vtd/Vts|.
Es cierto que han encontrado evidencia (3.4 sigma) de este proceso, pero no es evidencia de fisica mas alla del Modelo Estandar. La tasa observada es completamente compatible con la que esperamos en el Modelo Estandar.
Un saludo, Marcel Vos
Gracias, Marcel.
Hay que diferenciar la evidencia de una medida de la evidencia de Nueva Fisica. Esto es evidencia de una medida NO de Nueva Fisica. Por otro lado la predicción teórica involucra incertidumbres hadrónicas mucho mayores que para el caso b->s, pero es interesante.
Gracias, Joaquim.
Gracias por el blog y la tarea divulgativa que llevas a cabo.
Dicho esto, es importante aclarar que en esta entrada el resultado experimental ha sido malinterpretado. El cambio de título es un buen paso, pero el post sique conteniendo afirmaciones incorrectas, como por ejemplo: «Si esta señal alcanzara las 5 sigmas en LHCb (…) se trataría de la primera prueba de la existencia de nuevas partículas aún no descubiertas.» La predicción actual del Modelo Estándar es totalmente compatible con la medida, como se ha mencionado en los comentarios anteriores y en el paper experimental.
Obviamente podría haber una mejora de este cálculo teórico en el futuro que esté en discrepancia con la medida, pero eso es cierto para miles de medidas (cualquiera con una precisión mejor que el cálculo teórico).
Gracias, Martin, por tu comentario.