La masa del bosón de Higgs y del quark top (cima) apuntan a que el vacío del modelo estándar es metaestable, aunque no estamos del todo seguros porque está en el borde entre estable y metaestable. Además, los errores son muy grandes, tanto los experimentales, sobre todo en la masa del quark top, como los teóricos, hay que extrapolar los cálculos hasta la escala de Planck y las correcciones de mayor orden podrían ser importantes. Quizás sea por puro azar, o quizás haya algo profundo oculto, pero las masas del Higgs y del quark top parecen ajustadas en un punto crítico doble en relación a la estabilidad del vacío. Nos lo contó Pier Paolo Giardino (Univ. Pisa / INFN Pisa), «Is that a Standard Higgs? And now?,» CP³ Origins, slides pdf / video flash. Su artículo técnico es Dario Buttazzo, Giuseppe Degrassi, Pier Paolo Giardino, Gian F. Giudice, Filippo Sala, Alberto Salvio, Alessandro Strumia, «Investigating the near-criticality of the Higgs boson,» arXiv:1307.3536 [hep-ph].
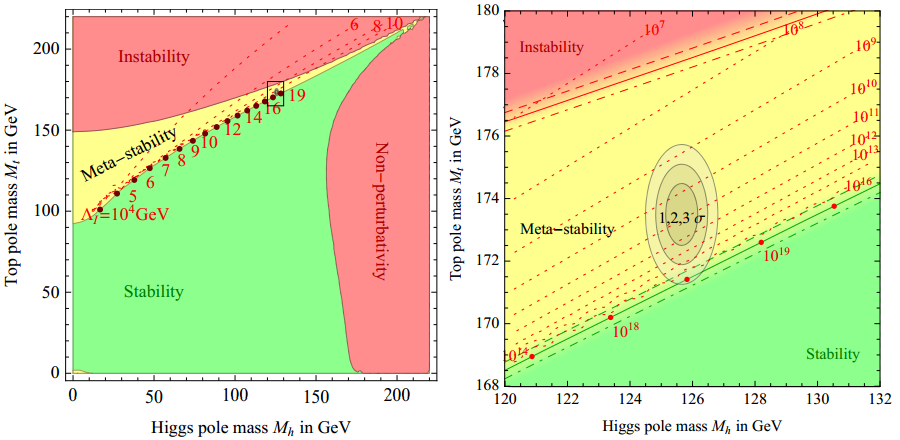
El vacío del modelo estándar viene determinado por el vacío del campo de Higgs. El potencial del campo de Higgs, el famoso sombrero mexicano, es V(H) = −½ m2(μ) |H|2 + λ(μ) |H|4), donde la masa m(μ) y la constante de acoplo λ(μ) dependen de la energía según las ecuaciones del grupo de renormalización. A alta energía el potencial se puede aproximar como V(H) ≈ λ(μ) |H|4, siendo el signo de λ(μ) el que determina la estabilidad del vacío del campo de Higgs y del modelo estándar. La función λ(μ) es monótona decreciente y parte de un valor inicial positivo λ(0)>0. El vacío es estable si λ(MPl )>0, donde es MPl es la energía de Planck, es inestable si λ(MEW)<0, donde MEW es la energía de la escala electrodébil, y es metaestable si λ(μ)=0 para algún valor de MEW < μ < MPl. Ya sabemos que el vacío no puede ser inestable, porque existimos. Los valores actuales de las masas del bosón de Higgs (125,66 ± 0,34 GeV) y del quark top (173,36 ± 0,65 GeV) indican que el vacío del modelo estándar es metaestable y λ(μ)=0 para 1010 GeV < μ < 1012 GeV. La mayor incertidumbre experimental se encuentra en el valor de la masa del quark top.
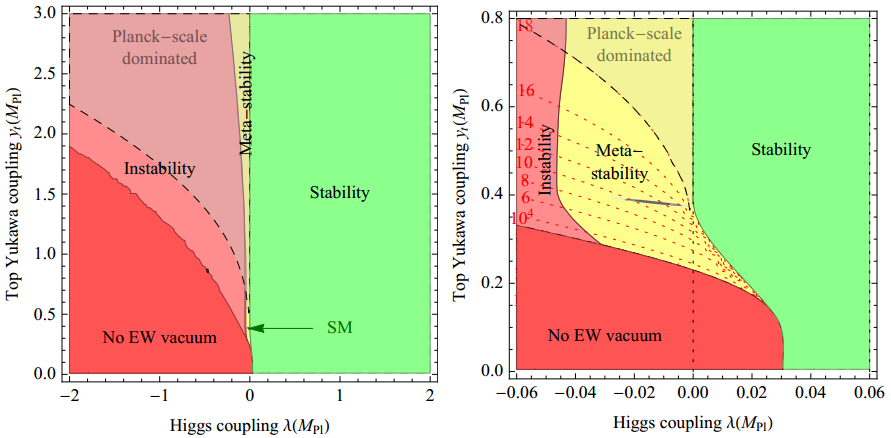
Esta figura muestra la estabilidad del modelo estándar en el plano definido por λ(MPl) y el acoplo de Yukawa para el quark top yt(MPl); la función yt(MPl) también es decreciente y parte de un valor yt(0) ≈ 1. La parte derecha es un zoom donde se puede observar una raya gris casi horizontal en la zona de metaestabilidad (en amarillo). Realmente parece que las masas del Higgs y del quark top están ajustadas para que el modelo estándar sea metaestable por alguna razón física.
Por supuesto, el cálculo teórico asume que el modelo estándar es válido hasta la escala de Planck (es decir, entre ~1 y ~1015 TeV), pero hay indicios indirectos de que no es así (el mecanismo del balancín (see-saw) en la física de los neutrinos, la existencia de la materia oscura, o la asimetría materia-antimateria). Por ello, el cálculo a la energía de Planck de los parámetros del modelo estándar mediante el grupo de renormalización hay que tomarlo con sumo cuidado. Recuerda que todos los parámetros del modelo estándar (constantes de acoplo y masas de partículas) cambian con la energía (μ).
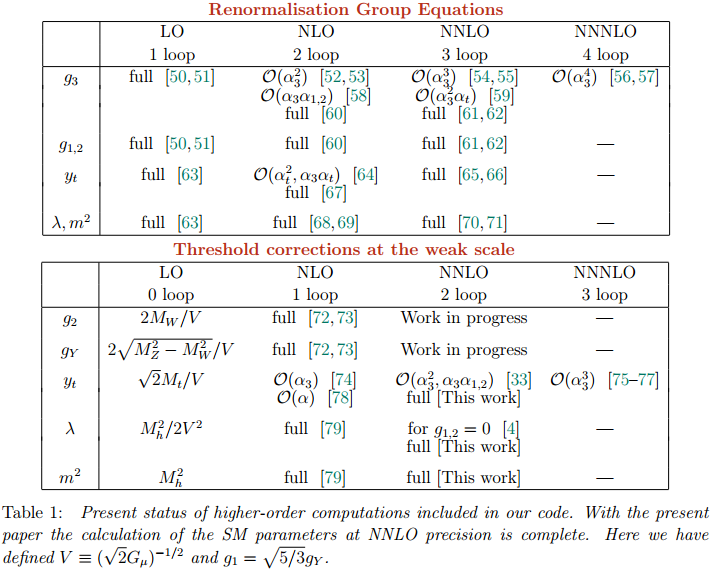
El cálculo teórico requiere determinar la evolución con la energía de seis parámetros (mostrados en esta tabla) hasta energías en la escala de Planck. En la actualidad el cálculo ha sido realizado sólo hasta el orden NNLO (hasta 3 loops) y se cree que las correcciones NNNLO serán pequeñas. Estos cálculos se realizan con la ayuda de ordenadores y no es fácil estimar cuándo estará listo el resultado hasta NNNLO.
El modelo estándar mínimo se basa en un potencial V(H) cuártico para el Higgs, pero nada prohíbe que el campo del Higgs sea más complicado a alta energía. La estabilidad del modelo estándar implicaría la existencia de otros mínimos locales a alta energía, lo que tendría la ventaja de que podría explicar la física de la inflación (es decir, el campo de Higgs sería el campo inflatón). Nuestro vacío sería el «verdadero vacío» (mínimo global) y el vacío a alta energía sería un «falso vacío» (mínimo local).
La metaestabilidad del modelo estándar a la que apuntan los datos actuales implica que vivimos en un «falso vacío» (mínimo local) y que existe un mínimo global del campo de Higgs a alta energía. Nuestro falso vacío, por efecto túnel, puede transitar al vacío verdadero. Este proceso debe ser muy poco probable, con una vida media mayor que la edad del universo (si no fuera así ya no existiríamos). ¿Cuándo puede ocurrir este proceso? No lo sabemos, podría ocurrir mañana mismo o dentro de unos cientos de miles de millones de años. Las estimaciones más «realistas» apuntan a que podría ocurrir en unas decenas de miles de millones de años. Pero todo esto es especulación científica pues no conocemos los detalles del potencial del campo de Higgs.
¿Qué pasará cuando el vacío metaestable pase por efecto túnel al verdadero vacío? Sidney Coleman (y físicos rusos) estudiaron este fenómeno a principios de los 1970. Resumiendo mucho, en el vacío se formarían (nucleación) burbujas de energía negativa cuyo radio crecería a la velocidad de la luz; cuando todas las burbujas colisionaran unas con otras se destruiría todo el universo conocido, aunque el universo como tal podría sobrevivir en su nuevo estado de vacío. Los detalles dependen de la cantidad de energía oscura que haya cuando se produzca el efecto túnel al nuevo vacío y de las características del vacío verdadero. Por supuesto, los cálculos de Coleman no tienen en cuenta el efecto a energías de la escala de Planck de la gravedad cuántica. No se conoce la teoría cuántica correcta de la gravedad, por lo que no podemos saber qué pasará, pero muchos físicos creen que el proceso se parará de alguna forma. Lo que pueda pasar más allá de este momento es pura especulación.




Comentario metafísico: ¿qué implicaciones para la Humanidad tendría poder demostrar que nuestro universo es realmente metaestable y que no pudiéramos parar algo tipo Big Rip o la transición al nuevo vacío? Cuando estaba en COU, pregunté una vez a mi profesor de Filosofía qué pensaba de los modelos cosmológicos que planteaban la existencia de una singularidad final (Big Crunch, circa 1996, aún no había dark energy, :P) para el dilema filosófico de la existencia humana en el Universo y la pregunta de si hay un «Gran Destino» al que podamos aspirar si realmente el tiempo de vida de todo el Universo es finito … Realmente, no me gustan algunas connotaciones religiosas que podrían venir del hecho del «día final del Universo»…
Por otra parte, ¿cuánto de seguros podemos estar de la metaestabilidad del vacío a este punto? El sector de Higgs apenas ha sido descubierto y falta explorarlo. Será un trabajo de varias generaciones, no de una sola. Y, como bien comentas, llega un momento en el que la gravitación cuántica entrará de alguna forma y nos dirá si esto es así (metaestabilidad) u ocurre algo realmente inesperado como una deceleración y un rebote…O cualquier otra posibilidad que ahora no podamos…
El conocimiento del destino del Universo depende, en el estado actual de las cosas, de la constante cosmológica. De momento parece que es un término constante, pero podría ser una energía fantasma, la quintaesencia, quintom matter, gas de Chaplygin o cualquier otra cosa que aún no hemos pensado…
Sobre la energía oscura, es realmente llamativo que el destino cósmico y la presencia de algún tipo de singularidad futura depende críticamente del modelo pero también del valor y signo de $latex omega$. Es necesaria una medida muy precisa para saber su valor, y aún así, puede llevarnos décadas afinar lo suficiente como para saber si es $latex omega =-1$ más o menos un error muy pequeño, y como el signo es crítico para determinar si es quintaesencia u otra, puede que tengamos problemas para decidir tal cuestión. LOs sucesores de Planck espero que con cosas tipo StateFinder y nuevas técnicas permitan discernir más sobre el misterio del término de presión espacio-tiempo que introdujo, por el motivo equivocado, Einstein pero que se ha demostrado crítico en lo que debe ser la nueva física y el destino del Universo…
Aclararé algo que creo que no precisé con lo yo quería decir acerca del signo. Distinguir el régimen fantasma de uno quintaesencia, si realmente estamos en uno de ellos, depende críticamente de «cuánto quintaesencia o fantasma es», y si es pequeño, y el error es grande, puede que tardemos aún bastante tiempo en distinguir críticamente si en vez de constante cosmológica es una de ellos porque si tenemos w=-1.1+-.2 o bien w=-0.9+-0.3 hacen compatible cualquiera de esos casos. Me pregunto cuándo se espera tener instrumentos para que el error en la medidad de omega permita discernir con claridad qué tipo de fluido es la energía oscura (constante cosmológica pura, quintaesencia, energía fantasma,…).
Pregunta: ¿alguien sabe qué sensibilidad se espera tenga James Webb en la medida de Omega (Lambda)?
Medir omega lambda es complicado, pero una medida fina de ella es necesario para determinar la naturaleza de la energía oscura. Espero verlo…
Amarashiki, James Webb (JWST) no está diseñado para estudiar la energía oscura y aportará muy poco a su estudio (algo similar a HST en supernovas Ia y en lentes gravitatorias). No he leído en detalle cual será su sensibilidad a Omega Lambda, pero será muy similar a la de HST, quizás un poco mayor porque abarca un trozo mayor de cielo, pero poco mayor. Hay instrumentos específicos.
Sabía que Webb no estaba diseñado para Dark Energy, pero desconocía si había algún programa en su tiempo de operación para hacer un estudio de la misma o qué sensibilidad, ya veo que no demasiada mejor que la de HST. ¿Quizás la NASA dedique alguno de los dos telescopios que le regaló Defensa para un estudio específico de energía oscura?
Me gustaría saber qué usos le darán a aquellos dos satélites/telescopios espía que el Pentágono tenía sin usar…
Para el estudio de la energía oscura, ESA está preparando la misión Euclid (http://sci.esa.int/euclid/), cuyo lanzamiento esta previsto para 2020. Copio del Assesment study Report:
«(1) Euclid will measure the dark energy equation of state parameters w_0 and w_a to a precision of 2% and 10% from the geometry and structure growth of the Universe.»
Bueno creo que dar por supuesto que la Física que conocemos actualmente es válida hasta la escala de Planck es bastante absurdo por lo que los cálculos bien podrían no ser correctos.
Me llama la atención como el principio antrópico cada vez parece más omnipresente: la metaestabilidad del vacío tiene que tener una probabilidad de transición lo suficientemente pequeña (sino no existiríamos), las constantes fundamentales tienen que tener un valor muy cercano al actual, la constante cosmológica tiene que ser ridículamente pequeña como la que observamos, las dimensiones (al menos las grandes) del espacio tienen que ser 3 como observamos sino la vida no existiría, la asimetría materia-antimateria debe ser la justa sino la vida no existiría… Reconozco que no me gusta mucho este «principio» pero es evidente que es cierto, que tiene que cumplirse. En mi opinión esto apunta a la existencia de un multiverso con distintas leyes físicas, quizás el «landscape» de la teoría de cuerdas existe en realidad en nuestro multiverso. Si la inflación es casi un hecho científico, existen muchas variantes que producirían un multiverso de forma «natural». El caso del multiverso probablemente estaría relacionado con el de dimensiones extra del espacio-tiempo, a veces me pregunto si no hemos «detectado» ya estas dimensiones aunque sea de forma indirecta aunque esto deriva una vez más en el debate de la relación entre matemáticas y física: por ejemplo, los espacios «espinoriales» en los que «giran» los electrones son espacios matemáticos abstractos pero TIENEN EFECTOS MEDIBLES físicamente y sus efectos contribuyen al momento magnético del electrón, si estos espacios tienen efectos medibles tienen que ser FÍSICAMENTE REALES, (o al menos tienen que tener algún aspecto de «realidad» ontológica) ¿Nuevas dimensiones? Como este ejemplo existen muchos otros, además, a medida que se añaden dimensiones extra aparecen propiedades sorprendentes: con 4 se unifican relatividad y electromagnetismo y con 11 (y solo con 11) parecen unificarse las 4 fuerzas fundamentales ¿Es esto solo una casualidad?
Como dijo el gran Carl Friedrich Gauss cuando utilizó los números complejos para demostrar el teorema fundamental del álgebra: los números complejos están en un grado de abstracción superior al de los números «reales» y pareciese que nosotros solo somos capaces de captar «las sombras» de este mundo complejo proyectadas en nuestro mundo «real»
¿Indicios de nuevas dimensiones?
Miguel, no sé qué conocimiento tienes de física y matemáticas. ¿Sabes lo que es la estabilidad de un sistema mecánico clásico? En la física de Newton los mínimos de la energía potencial determinan puntos de equilibrio del sistema que pueden ser estables o inestables en función del signo de la derivada del potencial en el mínimo. ¿Sabes por qué los mínimos de V(H)=H4 son estables y los mínimos de V(H)=-H4 son inestables? Necesito saber si lo sabes si tengo que escribir una entrada para legos en estas materias.
Esta más gracioso como trailer de pelicula en las trasparencias:
– Sería el Apocalipsis.
– Ah, sí, ese proceso eso ya lo estudio Coleman.
De todas formas, lo que parece demostrar este paper es que la física de particulas es capaz de predecir el valor de la escala de Planck (y de rebote, de la cte de Newton): aquella en la que tanto el acople cuartico del campo de higgs, lamba, como su renormalizacion, medida por beta(lambda), se hacen igual a cero. Me da a mi que es cosa de prejuicios el que se interprete al reves, como si la escala de Planck fuera lo fundamental e inamovible. Usease, ¿no queriais gravedad emergente? Pues tomad, escala de Planck emergente.
Me he reido un buen rato de tus últimas dos frases, lástima que con las fiestas de abajo de Móstoles (al lado de mi casa), los vecinos no se hayan enterado de mi grito «emergente»…
Mirad tambien la figura 3 (derecha) de http://arxiv.org/abs/1209.0393 Puede ser accidental, pero 4E17 GeV parece un punto bastante especial, aunque este todavia un poquitin lejos de los 1.2E19 GeV de la masa de plack, esta casi en la diana.
LHC reparació i 2016 les dades necessàries per a determinar Metaestabilidad – vixra 1309.0096