Aceptar que no hay ningún misterio. Más sencillo, imposible. Los átomos muónicos arrojan una valor de 0,84 fm (femtómetros) mucho más preciso que el valor de 0,88 fm según los átomos (electrónicos). Si aceptamos como correcto el valor de 0,84 fm para el radio de carga (RE) del protón se pueden recalcular todos los niveles electrónicos del átomo de hidrógeno (algunos cambian más de 10 kHz respecto al valor CODATA 2014). Si con los nuevos niveles se rehacen las estimaciones espectroscópicas del radio del protón en el hidrógeno (electrónico) se obtiene un valor entre 0,84 y 0,89 fm (según la técnica de interpolación usada, como muestra esta figura). Un valor compatible con las medidas en el hidrógeno muónico. Con lo que el problema del radio del protón desaparece.
Una regla no escrita de la física afirma que medir con un método diferente, pero mucho más preciso, conduce a un gran cambio en el valor medido. Así ha ocurrido muchas veces con muchas constantes fundamentales en el listado del Particle Data Group. Las medidas con muones son mucho más precisas que con electrones, porque su masa es 207 veces mayor y el átomo correspondiente es 207 veces más pequeño. Como son más precisas, lo justo es aceptarlas sin más como medidas mejores (máxime cuando el valor ha sido confirmado con el deuterio muónico). Quizás alguien piense que esto es como si aceptar pulpo como animal de compañía hiciera crecer la definición de animales de compañía hasta el punto de que hubiera que incluir entre ellos al pulpo. Pero la física experimental es así de sencilla y así de maravillosa.
Ni nueva física más allá del modelo estándar, ni violaciones del número leptónico, sólo aceptar que la física experimental es así (y siempre ha sido así). Repito, más sencillo, imposible. Los nuevos cálculos de los niveles atómicos con correcciones hiperfinas que dependen del radio del protón se han publicado en M. Horbatsch, E.A. Hessels, «A tabulation of the bound-state energies of atomic hydrogen,» Physical Review A 93: 022513 (2016), doi: 10.1103/PhysRevA.93.022513, arXiv:1601.01057 [physics.atom-ph]; las nuevas incertidumbres para las medidas en átomos (electrónicos) del radio del protón aparecen en M. Horbatsch, E.A. Hessels, «Evaluation of the strength of electron-proton scattering data for determining the proton charge radius,» Physical Review C 93: 015204 (2016), doi: 10.1103/PhysRevC.93.015204, arXiv:1509.05644 [nucl-ex].
Me he enterado de estos artículos al buscar información adicional para preparar el #Media2Ciencia para el próximo 14 de septiembre, #M2Proton, en el que participaré junto a Álvaro Peralta, @ribap, bajo la coordinación de Luis Quevedo, @Luis_Quevedo.
[PS 26 Ago 2016] Al final he añadido mi respuesta a un lector del blog sobre si esta solución ¿no es una tautología?
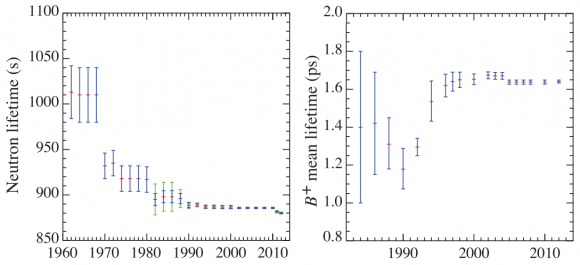
Esta figura muestra dos ejemplos del cambio del valor de una constante fundamental conforme se cambia a un método más preciso, en concreto, para la vida media del neutrón y para la vida media del mesón B. Ya lo he contado varios veces en este blog, pero ahora viene a colación gracias al estupendo artículo de Natalie Wolchover, «New Measurement Deepens Proton Puzzle,» Quanta Magazine, 11 Aug 2016. Natalie nos cuenta que la primera vez que se puso en contacto con Randolf Pohl (investigador principal del proyecto CREMA que estudia átomos muónicos) recibió como respuesta un listado de 12 figuras similares publicado por el Particle Data Group [PDF con las figuras].
Esta tabla ilustra algunos niveles electrónicos del átomo de hidrógeno calculados por Horbatsch y Hessels asumiendo que el radio del protón es 0,84 fm (valor CREMA) en lugar de 0,88 fm (valor CODATA). La última columna muestra la diferencia entre el nuevo valor CREMA y el valor previo CODATA (que no aparece en la figura). Como se ve hay diferencias de 15,3 kHz para los niveles S (n=1 y n=2), de 26,8 kHz para el nivel P (n=2) y de 11,9 kHz para el nivel D (n=3). Los interesados en tablas más extensas deben consultar su artículo en Physical Review A.
El cálculo preciso de la constante de Rydberg (que determina el radio de Bohr del átomo de hidrógeno) hasta una precisión de 1 kHz requiere incluir la estructura hiperfina de los niveles atómicos (desplazamiento de Lamb). Además de un valor muy preciso de la constante de estructura fina (α = 1/137,035 999 139(31) es el valor CODATA 2014), también hay que utilizar la masa del protón (mp/me = 1836,152 673 89(17), CODATA 2014), el momento magnético del protón (gp = 5,585 694 702(17), CODATA 2014) y el radio del protón (Rp = 0,8751(61) fm, CODATA 2014). Las nuevas tablas de Horbatsch y Hessels usan en este cálculo el valor del radio del protón Rp = 0,840 87(39) fm, obtenido por la colaboración CREMA (para la medida del radio del protón usando el hidrógeno muónico).
El nuevo valor de la constante de Rydberg es R = c R∞ = 3 289 841 960 248,9(3,0) kHz, que es mucho más preciso que el valor CODATA 2014 de 3 289 841 960 355(19) kHz. Usando este nuevo valor de la constante de Rydberg se pueden reinterpretar las medidas previas del radio del protón obtenidas tanto por espectroscopia, como por dispersión (scattering). De hecho, en el último artículo en Science del propio Pohl sobre el deuterio muónico se menciona que un cambio en la constante de Rydberg podría explicar el misterio del radio del protón.
En resumen, el principio de la navaja de Ockham afirma que ante dos soluciones a un misterio, la menos extraordinaria es la que debe ser preferida. Lo siento por quienes buscan nueva física por doquier. El problema del radio del protón no parece que vaya a ayudarles.
[PS 26 Ago 2016] Un lector de este blog me ha comentado por e-mail: «No entiendo. Si uno recalcula los niveles hiperfinos del átomo electrónico con el valor muónico del radio del protón y luego deduce de los mismos el radio del protón, ¿no es una tautologia que uno consiga algo compatible con el valor muónico?» Os comento la respuesta que le he enviado, que creo que puede ser del interés de todos.
No es una tautología porque lo que se hace es recalcular los errores sistemáticos. Recuerda que toda medida experimental tiene errores estadísticos y errores sistemáticos. A veces dominan unos, a veces los otros.
Las medidas del radio del protón usando átomos electrónicos usan los niveles de energía calculados a una precisión de 1 kHz, para lo que se tiene que usar el mejor valor del radio del protón disponible hasta entonces (que se había obtenido con medidas electrónicas). El resultado es una medida dominada por errores estadísticos. Sin embargo, los errores sistemáticos podrían haber sido subestimados.
Al usar el radio del protón usando átomos muónicos para evaluar los niveles de energía electrónicos se obtiene un resultado que también alcanza una precisión de 1 kHz, pero que difiere (en algunos niveles) a más de 10 kHz del valor que antes se pensaba que tenía un error de 1 kHz. Si se asume que estos nuevos niveles energéticos son más precisos (ya que la precisión del radio del protón obtenido con muones es unas 10 veces más precisa que con electrones), entonces resulta que había errores sistemáticos en las medidas electrónicas previas que no se habían tenido en cuenta.
Al reestimar los errores sistemáticos resulta que las medidas electrónicas del radio del protón resulta que son diez veces más grandes; luego las medidas electrónicas están dominadas por los errores sistemáticos y no por los estadísticos como se pensaba. Más aún, el nuevo intervalo de incertidumbre hace que dichas medidas sean perfectamente compatibles con las medidas muónicas. El problema es aparente y desaparece.
Te puede parecer una tautología, pero ha pasado lo mismo con las medidas de la vida media del neutrón (ahora sabemos que las de hace 50 años subestimaban los errores sistemáticos) y pasa de forma habitual en física de partículas (ejemplos famosos son la masa del quark top, la masa del Higgs, etc.). Se trata del pan de cada día de los físicos experimentales. Un nuevo método de medida más preciso muestra que los errores sistemáticos en los métodos de medida anteriores, menos precisos, estaban subestimados.




Esto si resulto ser algo mas complejo para mi
Muy buena (pregunta y) aclaración sobre la aparente tautología.
También hay un problema con el tiempo de vida medio del neutrón, dos experimentos, dos valores. Será que es un problema parecido? lo leí en alguna Scientific American.
Miguel, ese problema ya se resolvió. Lo tienes en una de las figuras del post. El artículo en SciAm que mencionas debe tener unos años.