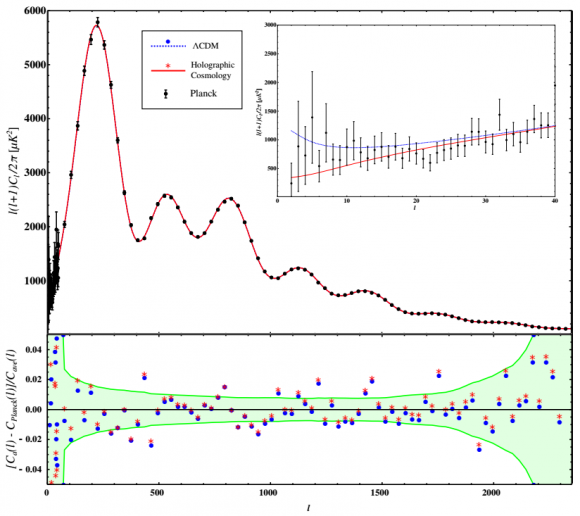
Habrás leído que se ha logrado la «primera evidencia de que nuestro Universo es un holograma» [EP, 30 Ene 2017]. En realidad se ha comparado el espectro multipolar del fondo cósmico de microondas de Planck 2015 con las predicciones de las dos fórmulas que aparecen en esta figura. La fórmula (1) es la predicción del modelo cosmológico ΛCDM. La fórmula (2) es la predicción genérica de un modelo cosmológico holográfico. Por supuesto, notarás que falta especificar g y β, que no son constantes, sino funciones, por ello la fórmula (2) debe ser acompañada de otras dos fórmulas. Al grano, el resultado de ambas fórmulas coincide para multipolos mayores de 30. Por debajo de 30 es cuestión de gustos saber cuál de los dos se comporta mejor, pues el error del espectro de Planck 2015 es enorme.
¿Significa esto que el modelo holográfico es mejor que el modelo de consenso? No, solo que bien ajustado permite entender el espectro multipolar del fondo cósmico de microondas. Otros modelos no lo logran, como la teoría TeVeS. ¿Podemos afirmar que el modelo holográfico es mejor? La navaja de Ockham exige comparar las fórmulas (1) y (2) para decidir qué modelo es más sencillo. Recuerda que la (2) además requiere otras dos fórmulas para g y β. ¿Cuál dirías que es mejor? La mayoría de los cosmólogos prefiere la fórmula (1). Lo siento por los aficionados a los titulares sensacionalistas, por ahora no podemos afirmar que el acuerdo entre la fórmula (1) y la (2) para multipolos mayores de 30 signifique se ha obtenido el primer indicio de que nuestro universo es un holograma.
El artículo es Niayesh Afshordi, Claudio Coriano, …, Kostas Skenderis, «From Planck data to Planck era: Observational tests of Holographic Cosmology,» Phys. Rev. Lett. 118: 041301 (27 Jan 2017), doi: 10.1103/PhysRevLett.118.041301, arXiv:1607.04878 [astro-ph.CO].
[PS 02 Feb 2017] Recomiendo leer la gran entrada de Enrique Borja, «Dualidad gravedad-teoría cuántica de campos: Universos y hologramas,» Cuentos Cuánticos, 31 Ene 2017. Explica muy bien el principio holográfico en el marco de la dualidad AdS/CFT, o gravedad/gauge. Y al final resume el nuevo resultado de Afshordi y sus colegas.
Esta figura ilustra el buen acuerdo entre los modelos cosmológicos y de consenso para multipolos mayores de 30. Para multipolos más pequeños el error de Planck es enorme. Más aún, ninguno de los dos modelos comológicos dan cuenta de las posibles estructuras que se atisban en el espectro. Casi seguro son estructuras ficticias, pero en cosmología se consideran anomalías que piden a gritos algún tipo de explicación.



Igual que vale para esa teoría, también se puede decir que vale para el ΛCDM porque los errores son tan grandes que ambas ajustan. La curva para multipolos altos además es exactamente la misma que la del modelo estándar -si se ha superpuesto sobre ella-, así que el parecido no sorprende para nada.
Veremos a ver; recuerdo además un artículo aquí en el que se establecían límites muy estrictos a la granularidad del Universo basado en estudios de fuentes de rayos gamma.
Exactamente U-95. Buen comentario 🙂 En realidad esa región es la única importante puesto que para multipolos bajos no sabemos mucho, luego no puedes decir que «uno es mejor que otro».
No sé… no se me hace del todo «limpio» meterte con el «régimen donde qft se vuelve no perturbativa» (por usar el lenguaje del artículo). No queda claro que sea directamente aplicable la correspondencia a nuestro universo temprano…
Sobre los experimentos de granulidad de espaciotiempo:
No sé en que contexto los citas pero es verdad que Francis ha hablado antes de ellos y son un problema para «teorías» como gravedad cuántica de lazos, pero no lo son para las ideas holográficas como ads/cft pues la teoría que vive en el bulk es invariante de Lorentz a toda escala de energía y no hay «espaciotiempo granuloso».
Hay preguntas mucho más concretas para describir correcta y eficazmente la física de los multipolos bajos como preguntarse por la teoría de gran unificación correcta (que es relevante para inflación), la naturaleza de dark matter, la posibilidad de supersimetría y sus relevancia para inflación etc. y y todos están dentro de las posibilidades de la teoría de perturbaciones para campos cuánticos incluso entender mejor la física estadística fuera del equilibrio puede arrojar mas luz para la física del universo temprano que hablar de cuestiones que no corresponden a una escala de energía en particular.
Definir exactamente en que escala de energía aparece la necesidad de una descripción genuinamente no perturbativa es un tema extremadamente delicado, muy especulativo y no se si venga bien al cuento meter en problemas al modelo cosmológico de consenso cuando LCDM funciona tan rematadamente bien.
Está claro que ADS/CFT es absolutamente importante para entender la física contemporánea. Desde las aplicaciones prácticas hasta lo que representa en la búsqueda de asuntos tan fascinantes como los vínculos entrelazamiento-espaciotiempo o la naturaleza de la gravedad. ¿Pero que de nuevo nos dice sobre la estructura en gran escala de nuestro universo? (Pueden remplazar aquí ADS por DS/CFT) debe ser algo muy sutil…
Pensaba que esos experimentos tenían algo que ver con el principio holográfico. Soy solamente un profano con los conocimientos de Física que se tienen de alguien que no pasó de empezar la carrera.
Si te sirve de consuelo, U-95, muchos de los que terminamos la carrera, también nos perdemos en la amalgama de teorías.
Está bien el comentario : ) son experimentos muy interesantes y son de lo poquísimo que tenemos en lo que respecta a fenomenología de gravedad cuántica.
Un poco de sal para bajar la presión… 🙂
Tengo una duda.
Supongamos que la teoría de 3D sin gravedad, la cual, es dual a la 4D con gravedad, funcionara bien para explicar nuestro universo ¿significaría eso que nuestro universo podría ser éste universo 3D, con sus características, tal cual, sin más, o sería necesario siempre que también existiera de forma subyacente otro universo con las caracterísiticas del 4D con gravedad?
Por que si se trata de lo segundo, pues la verdad, lo dual está muy bien para simplificar las mates, pero vamos, sería una realidad muy rebuscada.
¿Más rebuscada que una realidad 4D emergente de cuerdas? A mi entender la existencia de la frontera codificada implicaría la «proyección» del holograma, lo segundo emergería de lo primero inevitablemente.
Saludos.
¿Rebuscada? para nada.
Cuidado con lo de «Proyección» si entiendes por qué razón este uso de lenguaje está mal empleado entenderás algo importante de la correspondencia.
Entonces, Pelau, el universo 4D con gravedad del que emerge el 3D, ¿no tendría campos/partículas?,. es decir, ¿es más sencillo que el universo 4D que observamos a nuestro alrededor? Por que entonces sí que parece menos rebuscado como dices, un 4D con gravedad y una proyección en 3D con campos/partículas
¡uy! perdón por lo de «proyección». Quería decir, un universo pegadito en 3D con propiedades que…¿emergen del subyacente?
No quería ser pedante con la prohibición de usar la palabra «proyección». El punto es que en mi experiencia tal palabra confunde. Si piensas en Matemáticas y te fijas en dos espacios topológicos A, B y una proyección (Un mapeo A–>B que es sobreyectivo pero la imagen inversa de un punto en B no es un punto) entonces la proyección típicamente tiene buenas propiedades (es derivable, localmente su derivada tiene rango máximo etc.) pero con todo es muy mala idea para establecer una equivalencia entre dos espacios (como sea que lo entiendas).
El punto de Maldacena con ADS/CFT es una equivalencia completa en la física. Por un lado se estudia el límite de una teoría muy parecida a QCD en la que en cierto límite (número de colores grande) para su expansión perturbativa dominan diagramas (planares) que a cada orden tiene la misma forma (característica de Euler) que una superficie compacta con ese número de agujeros.
Es decir que la función de partición (para el vacío) de la teoría superconforme en dicho límite permite etiquetar cada término de su serie perturbativa con una superficie de Rieman, algo que es familiar en teoría de cuerdas. Ese fue uno de los primeros grandes hints de ADS/CFT.
Las funciones de partición de una teoría de gauge y de una teoría de gravedad son iguales : ) eso es lo bonito de la correspondencia : ) la igualdad. Es mas como un homeomorfismo : D (a nivel perturbativo) que una proyección 😉
No entiendo la pregunta Pedro.
Supongo que preguntas si existe una implementación del principio holográfico que modele a modele la evolución de nuestro universo. Tal cosa está muy lejos de nuestro entiendimiento actual.
¿Cuáles son algunas de las dificultades?
1.- La universalidad del principio holográfico. Este nace de la observación (clásica) de que la entropía de un agujero negro (el objeto más compacto posible) depende de su área. Pregunta (clásica): Toma una región cualquiera de espacio ¿Hay una de codificarla en la frontera de alguna variedad? No sabemos. Aunque con mucha seguridad se debe valer una cota entrópica tipo las que trabaja Bousso o al menos sabes que si deformas esa región a una maximalmente compacta su entropía dependerá como un área.
2.- La paradoja del Cortafuegos. Casi todo físico (razonable) al que le preguntes deberá decirte que «ser holográfica» es una propiedad deseable para una teoría cuántica de gravedad. Sin embargo si buscas en internet, grandes físicos como Polchinski o Mathur han hablado de la falta de eficacia de ADS/CFT para atacar la paradoja del cortafuegos o para detectar que subsector de la teoría conforme codifica los grados de libertad asociados a la singulariad de un agujero negro en un fondo ADS(5) x S^5 (o si se tiene por caso su inexistencia explicar como son regularizados). Quien sabe… tal vez ADS/CFT sea la máscara de un principio más profundo o tal vez la forma en que lo vemos ahora es muy primitiva.
3.- Nuestro universo es DS y no ADS. Claro que existe DS/CFT pero tal cual está no puede modelar nuestro universo simplemente por que el contenido de campos no concuerda (hay razones mucho más sutiles)
Y muchas más…
Pero hay una noticia interesante. La teoría de cuerdas es una teoría que usa de forma máxima el principio. Todas los objetos de la teoría están en cierto pie de igualdad, burdamente puedes decir que por transitividad todos están en pie de igualdad con la cuerda fundamental (o un agujero negro) que es una CFT en 2D en la hoja de mundo (en el caso del agujero este ya es «holográfico»), es decir: teoría de cuerdas es una realización máxima del principio que ¡además es implementado dinámicamente!
El principio holográfico está muy cerca de ser el principio guía tan buscado de la teoría de cuerdas. Si cuerdas describe nuestro mundo el principio holográfico tendrá una victoria «máxima».
😉
Gracias, Ramiro, la respuesta a mi pregunta, por lo que comenta Pelau, y con por lo que comentas tú, es que un universo 3D sin gravedad con campos/partículas, podría ser el nuestro, siempre y cuando esté pegado a uno 4D con gravedad, necesario para obtener todas las propiedades que encontramos al rededor. Había pensando que la dualidad entre ellas podría significar en que cada uno de ellos, por separado, podría emeger las propiedades que encontramos en el nuestro; error, mal, muy mal.
Lo que quise decir (la redacción me quedó algo confusa) es que si hay una frontera, entonces inevitablemente hay un holograma. Por eso dije «proyección», en el sentido de nuestros hologramas 3D que son una proyección de slides 2D. Lo hice para enfatizar que si cabe hablar de un orden jerárquico, si un universo emerge del otro, el más simple (3D) me parece más fundamental, el emergente sería el holograma 4D.
Pero Pelau, ¿no sería más exacto decir que lo que emerge son las propiedades que se observan dentro del universo de 3D, en vez de decir que es el propio universo 3D el que emerge?
Pedro, es que yo nunca dije que el universo 3D (frontera) emerja del universo 4D (con gravedad), al contrario.
De hecho todo el asunto debe ser conjugado en tiempo condicional, con un gran «Si interpretamos que tal cosa… entonces tal otra…»
Como dice Ramiro más arriba, en la correspondencia ADS/CFT ambos universos están en pie de igualdad. Si uno existe el otro también y son equivalentes.
En tu primer comentario dices que esa realidad dual te parecería muy rebuscada. Te respondí con una pregunta que pretendía ilustrar que esa realidad no sería más rebuscada que una realidad 4D emergente de cuerdas (y me refería a las más simples, las cuerdas 1D, no a las P-branas ni D-branas).
Ahí se me coló el factor «emergente» en el discurso y por escribir apurado generé confusión. Así pues, conjuguemos de una vez por todas este asunto en tiempo condicional:
Si interpretamos la metáfora holográfica en términos de un holograma real, igual que uno de nuestros hologramas 3D de luz cuya información está codificada en una placa 2D… ahí cabe decir que la placa 2D es más fundamental que su proyección 3D… el holograma volumétrico emerge de la placa 2D.
Eso, claro está, si no tenemos en cuenta el hecho de que la placa 2D fue obtenida escaneando un objeto 3D en primer lugar, pero eso no viene a cuento ahora. Mi intención fue establecer una limitada analogía.
Es decir, análogamente a un holograma 3D emergente de una placa 2D, y siempre en tiempo condicional, el universo 4D (con gravedad) emergería del universo 3D (frontera).
En otras palabras, si pensamos en términos de que nuestro universo físico 4D emerge de «un set de leyes naturales», entonces lo más sensato sería pensar que esas «leyes naturales» están «codificadas» en el nivel de complejidad más simple de todos.
Insisto en que no es más que una analogía, limitada, traicionera. Hasta ahí.
Saludos.
Por nada Pedro 😉
Un comentario más off-topic:
Si piensas en holografía desde el punto de vista de matemáticas es algo sumamente extraño. Te diré unas razones dichas de modo grosero y bastante impresiso.
Imagina que tienes una variedad diferenciable con frontera no vacía. Si te fijas en las funciones diferenciables que extienden de la frontera a toda la variedad estás tienen grado cero (Es decir: son hasta deformaciones diferenciables una constante) y en el caso de ADS/CFT los mapeos entre ambos lados de la correspondencia son altamente no triviales incluso si en el ejemplo de las variedades piensas en un funtor que asigna un espacio de Hilbert a variedad y frontera encontrás un razonamiento parecido. Luego eso de la holografía no es un asunto tan ingenuo, hay gente que se pregunta sinceramente si algo como el teorema de Gauss en cálculo elemental o la formula integral de Cauchy no son de alguna manera «Princpios holográficos» la respuesta es un rotundo: NO. Si piensas detenidamente porque no lo son descubrirás porque Holografía es algo profundamente no trivial y que no tiene buenas analogías con ningún fenómeno matemático (que mi ignorancia sepa) explicable a nivel elemental.
Saludos
Interesantes comentarios Ramiro. Es posible que la dualidad ADS/CFT sea solo «la punta del iceberg» de algo más profundo. Ciertos trabajos relacionados con teorías de alto spin especulan con que la dualidad podría relacionar distintos espacio-tiempos que en realidad forman el mismo «twistor space». Sea como sea es sin duda uno de los avances teóricos más grandes de las últimas décadas.
No problema pelau 😉
No pretendía ser pedante, supongo que todos los que estamos aquí somos entusiastas, es bueno auto-ayudarse con analogías y tratar siempre de pensar, leer o calcular mas para mejorarlas.
Supongo que hasta a los profesionales les pasa 🙂 y que bueno… de eso se trata
Descuida, Ramiro, se nota a la legua quién viene con buena onda y quién no, y tú de pedante nada, al contrario, siempre enriqueciendo el hilo codo a codo con planck, no hay palabras para agradecer vuestros aportes.
En todo caso, ¿qué es peor, pecar de puntilloso o distorsionar el asunto hasta traicionarlo? Si poner las cosas en su justo lugar es ser pedante, pues ya quisiera yo más pedantería de ese tipo por aquí 🙂
Saludos.
Gracias por tu amabilidad, pensamientos y comentarios Pelau.
Un placer compartir el mismo gusto por estas cosas. No dejes de leer a Francis y de fascinarte con aprender más de la naturaleza.
Supongo no hace falta aquí decirlo.
Una forma quizás más intuitiva de entender la dualidad ADS/CFT: Una teoría CFT en nuestro espacio-tiempo 4D tiene una serie de simetrías que están generadas por 15 operadores: 6 generan la simetría Lorentz, 4 generan las simetrías de traslación y los 5 restantes generan la simetría conforme. Estos 15 operadores definen un álgebra de Lie en 4D, lo increíble es que ¡Un espacio-tiempo ADS en 5D está generado por los mismos 15 operadores y el mismo álgebre de Lie! ¡Esta es una de las bases de la dualidad ADS/CFT!
Siempre esclarecedor y estimulante. Muchas gracias, planck.
Justo así es como se debe entender.
Que bien que la discusión termine con el fantástico comentario de planck. Es extremadamente útil (y correcto) mirarlo así.
1.- «Del lado de la CFT» la simetría conforme es una simetría de los campos. «Del lado del mundo ADS(5)» da la «casualidad» de que el grupo de isometrías del espacio tiene es el mismo que el grupo de transformaciones conformes de los campos. ¡¡Que misterioso eso de igualar las simetrías internas y las simetrías del espacio de forma literal!! 🙂 ¿Os recuerda algo?
¿En qué ayuda verlo así?: Ayuda porque esa observación es la que hace tan difícil generalizar la correspondencia. De manera ingenua: Si quieres dar otro ejemplo de la correspondencia tienes que encontrar un espacio con un grupo de simetría razonable e identificarlo con alguna simetría de una teoría del campo (y posiblemente tomar productos con otros espacios para tener más isometrías e igualar los grados de libertad bosónicos y fermiónicos de la teoría del campo como se hace al tomar el producto de ADS con S^5). En general los espacios pueden tener formas muy complicadas y en general no vas a encontrar una teoría tan simétrica, bien comportada (¡e integrable!) como N=4 SYM.
Así se puede resumir tanto el milagro ADS/CFT como el problema de generalizar.
El comentario es intuitivo, en realidad lo importante son las simetrías asintóticas del espacio pues ads/cft funciona para deformaciones de ads, incluso puedes deformar el espacio para que contenga un agujero negro, varios de ellos, D3-branas, cuerdas negras o varias de ellas. Lo importante es mantener las simetrías asintóticas y eso es genial porque si equiparas una teoría con un agujero negro a una teoría unitaria que no lo tiene entonces aparentemente una pista de que la paradoja de la información se resuelve indicando que no hay pérdida… aparentemente (es extremadamente fascinante entender las sutilezas de esto). Por otro lado no es un gran consuelo puesto que las simetrías asintóticas son un problema, ADS funciona de maravilla porque se pueden definir teorías del campo de la forma en que lo hacemos siempre (suponiendo que lejos de la zona de interacción los estados del campo se comportan como libres, encontrar la fórmula de LSZ y calcular amplitudes), un agujero negro en ADS no es muy diferente de un agujero negro encerrado en una caja (entiéndase en equilibrio con su radiación hawking). Pero por citar un ejemplo: Nuestro universo es asintóticamente De-Sitter, este es un espacio compacto y pongas el campo que pongas en dicho espacio no puedes proceder como siempre lo hacemos (que de hecho es la única forma en que sabemos hacer QFT) no puedes suponer que el campo tiene estados asintóticos libres… ¡¡En un espacio de De Sitter una QFT es siempre SIEMPRE interactuante!… es sólo un ejemplo de porque es difícil dar otros ejemplos.
Saludos planck
Me olvidé de lo más importente jejeej
Verlo como lo dice Planck es mejor al ejemplo que yo di.
Yo cite una observación que compara el límite de baja de energía de una teoría y perturbaciones (pequeñas) de un sector especial de otra. Los grandes físicos de nuestros tiempos creen firmemente que la correspondencia es algo que se cumple exactamente (de forma no perturbativa). No sólo en ciertos límites de estas al contrario: se cumple siempre. Y el punto de planck es independiente de límites. Es general.
«Por supuesto, notarás que falta especificar g y β, que no son constantes, sino funciones»
:-), en mi caso no.