Un objeto real tiene propiedades con valores bien definidos independientemente del orden en que sean medidas. La mecánica cuántica no es una teoría realista. Un sistema cuántico puede presentar propiedades cuyo valor medido depende del orden en el que sean medidas. Lanzas un cubilete con dos dados «cuánticos.» El valor que saldrá en cada dado es diferente si observas ambos dados simultáneamente o uno a uno. Técnicamente, la mecánica cuántica es contextual. El contexto de la medida (cómo se realiza ésta) influye en el resultado obtenido. Así lo han demostrado experimentalmente el sevillano Adán Cabello y sus colaboradores austríacos en el artículo técnico G. Kirchmair et al., «State-independent experimental test of quantum contextuality,» Letter, Nature 460: 494-497, 23 July 2009, como nos cuenta Boris Blinov, «Quantum mechanics: Hidden context,» News and Views, Nature 460: 464-465, 23 July 2009.
Un sevillano publicando en Nature es motivo suficiente para que muchos medios se hayan hecho eco de esta noticia. Por ejemplo, «Mediciones cuánticas: el sentido común no es suficiente,» Servicio de Información y Noticias Científicas, SINC de la FECYT, 22 julio 2009, «Un equipo internacional de físicos ha realizado en Innsbruck (Austria) un experimento con parejas de iones en el que se muestra que, independientemente del estado en que se preparen los iones, es imposible explicar lo que se observa en términos no contextuales, es decir, suponiendo que los resultados no dependan de otras mediciones compatibles que se hagan sobre el sistema.» Kanijo ha «fusilado» la noticia (no ha tenido ni que molestarse en traducirla). Y cómo no, ha sido meneada. Muchos otros se harán eco de esta noticia y la Francis, cual mula, no puede ser menos.
Kirchmair y sus colaboradores utilizan una técnica de medida sin demolición (QND o quantum non-demolition) que a diferencia de las medidas estándares no provoca el colapso completo (demolición) de la función de onda cuando esta representa estados entrelazados superpuestos. Este proceso es clave en el diseño de ordenadores cuánticos, donde las puertas lógicas cuánticas deben ser capaces de leer el estado de un cubit sin afectar a los demás en un registro de varios cubits. Como el gato de Schrödinger que está simultáneamente vivo y muerto (<vivo>+<muerto>), con dos dados «cuánticos» entrelazados tendríamos 36 posibles estados superpuestos (simultáneos) según la pareja de caras que salga al tirarlos <1,1>+<1,2>+…+<6,6>. Con una medida QND podemos medir uno de los dados sin destruir el estado de superposición obteniendo un nuevo estado <1,k>+<2,k>+…+<6,k>, donde <k> es el estado medido en el primer dado.
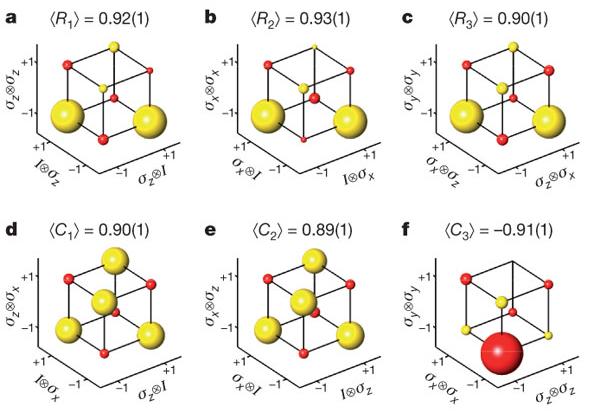
Kirchmair y sus colaboradores han estudiado experimentalmente una desigualdad de tipo Bell presentada en 1967 por Kochen y Specker para verificar la no contextualidad de la mecánica cuántica. Ya se demostró una desigualdad más sencilla, de Clauser-Horne-Shimony-Holt, que afirma que <A,B>+<C,D>+<A,C>-<B,D> <= 2, para toda teoría de variables ocultas, desigualdad que se viola desde el punto de vista cuántico, pero que aporta poco sobre el problema de la contextualidad. Kirchmair et al. han considerado estados <v1,v2,v3> donde vi es un valor en A,a,a,B,b,b,C,c, y c, y la desigualdad <A,B,C>+<a,b,c>+<a,b,c>+<A,a,a>+<B,b,b>-<C,c,c> <= 4, para toda teoría de variables ocultas, pero que la mecánica cuántica viola, resultando en un valor mucho mayor (las medidas de un valor de 5.46 +/- 0.03). [Para los que no entiendan la fórmula, donde <,> es la correlación]. Este tipo de estados permiten estudiar la contextualidad ya que se puede realizar hasta 3 medidas QND en 6 modos diferentes, que conducen a incumplimientos diferentes de esta desigualdad. Experimentos anteriores ya habían verificado la desigualdad (teorema) de Bell-Kochen-Specker. ¿Qué es lo nuevo? Los investigadores han demostrado que el resultado cuántico es independiente de cómo se preparen inicialmente los estados en superposición (y lo han demostrado con una certeza del 99% utilizando 10 formas diferentes de prepararlos).
Bohr vuelve a vencer a Einstein. Otra demostración más de que no hay ninguna teoría de variables ocultas clásica subyacente a la mecánica cuántica. ¿Qué queda por hacer en el futuro? Habrá que repetir este experimento con un nuevo diseño que permita que los estados en superposición se encuentren separados a una distancia suficientemente grande como para que actúe la no localidad de la mecánica cuántica.
¿Para qué sirve este trabajo de investigación? Su utilidad más directa es en sistemas de cifrado cuántico (basados en el transporte de portadores con tres estados cuánticos) o en las tecnologías de procesamiento de información cuántica que habrá que desarrollar en el camino hacia los futuros ordenadores cuánticos.

