[youtube=http://www.youtube.com/watch?feature=player_embedded&v=N7b0cLn-wHU#!]
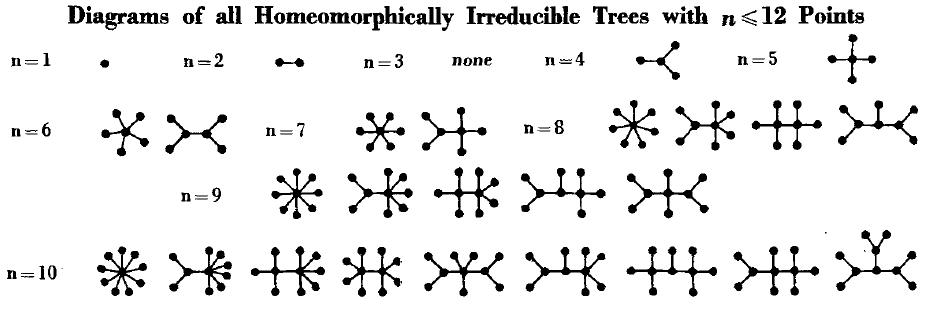
Esta escena de la película «El indomable Will Hunting» (título original «Good Will Hunting») de 1997, dirigida por Gus Van Sant y protagonizada por Matt Damon y Ben Affleck (en la que también aparece Robin Williams) describe un problema matemático de la teoría de grafos: dibujar un sistema de representantes de las 10 clases de árboles con 10 vértices homeomórficamente irreducibles. La solución de este problema fue obtenida por Frank Harary, Geert Prins, «The number of homeomorphically irreducible trees, and other species,» Acta Mathematica 101: 141-162, 1959 [copia gratis]. La solución a este problema para árboles con hasta 10 vértices aparece en la siguiente figura, extraída de dicho artículo (en formato un poco más compacto).
En teoría de grafos, un árbol es un grafo en el que cada par de vértices está conectado sólo por un único camino. Una definición más técnica nos dice que un grafo simple no dirigido G con un número finito n de vértices es un árbol si cumple cualquiera de las siguientes condiciones (todas equivalentes entre sí): (1) es conexo y tiene n-1 aristas, o (2) es conexo y no tiene ciclos, o (3) tiene n-1 aristas y no tiene ciclos, o (4) existe una única trayectoria entre cada par de vértices [gracias Alberto por el comentario de más abajo]. El grado de un vértice es el número de aristas a las que está conectado. Una «hoja» es un vértice de grado 1. Un vértice interno es un vértice de grado mayor que 1. Un árbol es irreducible si no tiene vértices de grado 2.
En esta figura, el único árbol irreducible es el de n=4, ya que los de n=5, 6 y 7 vértices todos se pueden reducir a dicho árbol eliminando los vértices de grado 2 que están marcados con una circunferencia en color rojo. Obtener todos los grafos con 10 vértices que son irreducibles no es difícil y cualquiera tanteando un poco puede hacerlo. Obviamente, lo más difícil es demostrar que no existe ningún otro.
¿Te atreves a dibujar todos los árboles irreducibles con n=11? No te pide que demuestres que tu lista es completa, sólo que lo intentes. No es un problema difícil (no creo que te requiera más de una hora de trabajo). Si lo haces te sentirás como Matt Damon (o como Will Hunting) Por supuesto, puedes chequear tu respuesta con el artículo original (que presenta los grafos irreducibles hasta n=12); también, hay programas de ordenador en la web que te permiten dibujarlos (si te gusta programar en Mathematica este problema es bonito para resolver por uno mismo sin buscar el notebook en la web). ¿Eres profesor de matemáticas? Por qué no le propones este problema a tus alumnos (resuelves el caso hasta n=6 y les pides a los alumnos que tanteen los casos n=7 u n=8).
Esta entrada participa en la Edición 4.1 del Carnaval de Matemáticas cuyo anfitrión es Tito Eliatron Dixit.



Gracias por la entrada, pero una pequeña puntualización:
La definición «más técnica» de árbol no es del todo precisa (no es necesario que se den todas las condiciones, ya que se implican entre si).
Así por limitarme a las condiciones que pones:
a) conexo
b) n-1 aristas
c) sin ciclos
d) existe una trayectoria única.
a+b, a+c, b+c , d son condiciones equivalentes y cualquiera de ellas vale como definición de árbol (o de caracterización).
Gracias, Alberto, lo arreglo. He escrito la entrada demasiado rápido y sin pensar.
Como supongo sabes, le dediqué una entrada a esto en mi blog, hace ya tiempo, aquí:
http://thespectrumofriemannium.wordpress.com/2012/11/27/log055-will-hunting-problems/
Confesión: resolví este problema mientras me saltaba unas aburridas clases de asignatura X durante tercer año de carrera…
Detestaba tanto las formas de dar clases de algunos profesores… Yo dibujé hasta los homeomorficamente irreducibles de grado 14, los 78, en 7 u 8 páginas…Y ya no continué…Porque sabía la «receta»…Y el siguiente grado (15) daba para mucho más…
Ya que estamos, ¿alguien conoce software libre para Linux sobre grafos?
De hecho, como es bien conocido por expertos en teoría de grafos, la función generatriz para los árboles irreducibles de grado n ( n puntos o vértices) está dada por la expansión polinómica:
$latex h(x)=x+x^2+x^4+x^5+2x^6+2x^7+4x^8+5x^9+10x^{10}+14x^{11}+26x^{12}+42x^{13}+78x^{14}+132x^{15}+mathcal{O}(x^{16})$
Muy buen pasatiempo y motivación adicional para cualquier niño que se divierta con las mates (y para mí). Un pequeño apunte: en la imagen falta el último diagrama en el caso n=10. No será especialmente relevante, pero por un momento ha hecho que se tambaleara mi concepción de los árboles irreducibles hasta que lo he mirado en el original. Y, por supuesto, gracias por la entrada.
Muy bien, Horembheb, prueba superada… fue intencionado (igual que dejar el título con n <= 12), pensé ¿a ver quién se da cuenta? Por cierto, en la pizarra de la película (vídeo youtube) faltan dos diagramas (uno de ellos el que yo he omitido)…
Francis, me sale un grafo más con 10 nodos que no veo en tu solución, se te ha pasado incluirlo o lo tengo mal yo?
Un saludo 🙂
Pd: enserio dicho problema no fue resuelto hasta hace 50 años?
Luca
Muy bien, Luca, lo has descubierto. Falta a propósito. El problema no fue resuelto hasta que a alguien no se le ocurrió resolverlo…
Proposición 4.1. Dado un grafo no dirigido G = (N, M), las siguientes propiedades son
equivalentes:
(i) G es un árbol
(ii) G es conexo y tiene n − 1 aristas.
(iii) G no tiene ciclos y tiene n − 1 aristas.
(iv) G no tiene ciclos y, si añadimos una arista cualquiera, se formará un ciclo (y sólo uno).
(v) G es conexo y, si eliminamos una arista cualquiera, deja de ser conexo.
(vi) Cada par de nodos de G están unidos por un único camino.
Demostración. Todas las equivalencias son muy sencillas de demostrar. Por ejemplo, veamos
que (I) implica (VI). Como un árbol es necesariamente conexo, hay al menos un camino entre
cualquier par de vértices. Supongamos que hay más de un camino entre un par de vértices.
Entonces, la cadena que resulta de concatenar estos dos caminos tendrá un ciclo. Pero un árbol
no contiene ciclos. Por lo tanto, debe haber un único camino entre cualquier par de vértices de
un árbol.