Las gotas danzantes son un análogo clásico a la teoría de la onda piloto (o interpretación causal) de la mecánica cuántica. Un nuevo artículo estudia la fuerza mutua entre varias gotas que se mueven en fila en una cavidad anular. Se mueven de forma colectiva (coherente) manteniendo constante su separación mutua y con una velocidad de grupo mayor que la velocidad de cada gota individual. Los autores del estudio interpretan el resultado como que la distancia mutua entre las gotas está cuantizada.
El artículo es B. Filoux, M. Hubert, N. Vandewalle, «Strings of droplets propelled by coherent waves,» arXiv:1504.00484 [physics.flu-dyn]. Página web del grupo de investigación |Q>uandrops. En mi blog puedes leer «Por qué las gotas danzantes simulan la mecánica cuántica,» LCMF, 24 Feb 2014.
Una pequeña gota de aceite de silicona (viscosidad η = 20 cSt) oscila en vertical y se mueve en horizontal cuando se coloca sobre una superficie líquida de aceite de silicona que vibra (siempre que la vibración Γ se encuentre en cierto intervalo ΓB < Γ < ΓF). La capa de aire entre la gota y la superficie líquida impide la coalescencia. En función de la frecuencia de vibración Γ se observan diferentes comportamientos que imitan el comportamiento cuántico de una onda piloto de DeBroglie–Bohm. Estas gotas se llaman walkers y muestran fenómenos análogos al efecto túnel, difracción y interferencia, niveles energéticos discretos, etc.
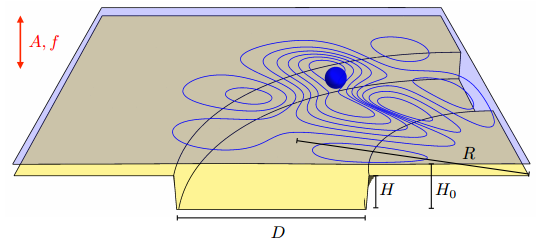
En el nuevo trabajo se estudia una cadena de gotas danzantes que se mueven en una cavidad en forma de anillo con frecuencia próxima a la máxima (límite de estabilidad), Γ = 0,95 ΓF. La longitud de onda de Faraday, que se asemeja a la longitud de onda de Compton en mecánica cuántica, es de λF ≈ 6 mm. En el centro del anillo la profundidad del líquido es H = 4 mm y la anchura del canal es D = 7,5 mm. Fuera del anillo la profundidad del líquido es de 1 mm; la cavidad confina las gotas, aunque no evita que haya cierta probabilidad de que la abandonen (que los autores interpretan como efecto túnel).
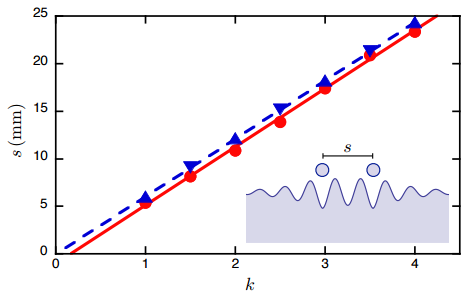
Para el forzamiento usado, la velocidad de una sola gota en el anillo es de v1 ≈ 10 mm/s (siendo independiente del radio del anillo). Cuando se colocan N gotas se mueven de forma colectiva con una distancia constante que sigue la fórmula lineal s = (k − k0) λF, donde λF = 6,1 ± 0,1 mm, k0 = 0,18 ± 0,02 y k es un número semientero que etiqueta el modo de vibración (la separación entre las gotas es k λF, luego el inciso muestra un ejemplo de k=2). Para k entero las gotas se mueven de forma síncrona y para k semientero se mueven de forma antisíncrona. El caso k = 1/2 está prohíbido, ya que en dicho caso las gotas se ponen a orbitar una alrededor de la otra en una trayectoria complicada y al final se produce su coalescencia o su desaparición.
Cuando se introducen dos gotas en el anillo con k=2 la velocidad de su centro de masas común crece conforme su distancia decrece; como muestra la figura izquierda, crece hasta un 12% cuando su distancia mutua es de 5 mm, siendo sólo un 4% mayor cuando la distancia es de 20 mm. El número máximo de gotas separadas por una única longitud de onda λF que caben en el anillo estudiado es de 12. La figura derecha muestra que la velocidad colectiva de una cadena de 11 gotas con k=1 (en crestas consecutivas) es un 12% mayor que la de una gota individual. Los autores del estudio han obtenido un modelo matemático clásico que permite estimar esta velocidad con precisión (la curva azul con triángulos sólidos ha sido obtenida con simulaciones numéricas de este modelo). Como se puede observar el modelo captura el comportamiento cualitativo y se requieren modelos mejores para capturar el comportamiento cuantitativo observado (quizás la adición de algún efecto clásico de tipo memoria o el desarrollo de un modelo cuántico).
En resumen, un trabajo interesante que disfrutarán los físicos alucinados con las gotas danzantes, los walkers. Los resultados presentados piden a gritos un modelo matemático más detallado. Quizás alguno de los lectores de este blog se atreva a proponer uno. ¿Será un modelo cuántico? ¿Hasta dónde nos llevará la analogía con la mecánica cuántica en este sistema clásico?




Que interesantes las sugerencias de estos estudios de microfluídica, que teóricamente podrían reducir la mecánica cuántica a mecanismos clásicos. Habría que suponer que el «vacío» no seria tal sino un super-fluido.
Un paso mas hacia la «clasizacion» de la fisica. Acá están diciendo que el espacio tiempo no es espumoso: http://www.abc.es/ciencia/20150317/abci-estructura-espacio-tiempo-espumosa-201503171146.html
Juan, en mi blog puedes leer dicha noticia en «Restricción experimental a la escala de energía de la espuma cuántica de Wheeler» https://francis.naukas.com/2015/03/17/restriccion-experimental-a-la-escala-de-energia-de-la-espuma-cuantica-de-wheeler/
Esto me recuerda la intuición «fluídica» que siempre tuve acerca de la gravedad.
Esta:
Juguemos un momento a Dios e imaginemos una tabula rasa de espacio vacío (que no tiene
sentido sin materia, dicen, pero vamos a ignorar eso un rato) y llenemoslo, como por arte de magia, con un “medio” formado por partículas M muy pequeñas.
Dentro del “medio” debe haber otras partículas tipo N mucho mas grandes (por 9 órdenes de magnitud, la diferencia entre una molécula de agua y una pelota de fútbol) que reaccionan ante el “medio” como si este fuera un fluido.
Las partículas N siempre se mueven hacia los volúmenes de menor presión del “medio”.
Supongamos una fuente de ondas de presión, es decir, algún mecanismo F que esta produciendo las ondas.
Estas ondas deben ser longitudinales y aproximadamente triangulares. Debe haberlas de dos clases: 1)con frente de ataque corto y abrupto y decaimiento largo y 2) al revés: con frente de ataque largo y decaimiento corto. Su longitud y amplitud deberían ser significativamente más grandes que las partículas N, como para afectar su posición. Por ejemplo, 100 veces mas largas y 10 veces mas altas.
Cuando una partícula N recibe una onda de presión tipo 2, “percibe” primero el frente de ataque, de pendiente suave. Como la diferencia de presiones entre los extremos de la partícula no es lo suficientemente elevada, entonces no se mueve.
Pero cuando pasa la cúspide de la onda y llega el decaimiento, como este decaimiento es más inclinado (y corto), la diferencia de presiones es suficiente para mover la partícula N. ¿Y hacia donde se mueve? Hacia la zona de menos presión, por supuesto, es decir, hacia F.
Las sucesivas ondas atraen de a pequeños saltos la partícula N hacia F. Sin embargo, no termina de acercarse nunca: N llega a una distancia de F tal que el frente de onda “suave” tiene mas pendiente porque la amplitud de la onda es mayor (por hallarse mas cerca de la fuente) y la diferencia de presiones es suficientemente acusada como para rechazar a N.
De ese modo, la distancia de N a F queda oscilando dentro de un rango. Asi tendríamos una onda de atracción… acotada. Aunque desde el punto de vista de una escala superior, parecería que M se “pega” a F (como una mesa al piso).
Por ese mismo mecanismo una onda de tipo 1 rechazaría la partícula N: sería una onda de repulsión. La sensibilidad de la partícula N a estas ondas dependería de su masa, su tamaño, la longitud y amplitud de la onda. Es decir que si poblamos el medio con otras partículas mas variadas, solo una fracción reaccionara a una onda dada. O dicho de otro modo: podrían coexistir muchos tipos de partículas sensibles (atractiva o repulsivamente) a ciertas frecuencias/amplitudes de ondas pero no a otras.
Para un observador imaginario formado por estas partículas N, parecerían existir distintos campos de fuerza.
Por otro lado, si la gravedad funcionara como una onda tipo 2, su “target” debería ser alguna partícula elemental de la materia tan pequeña que incluso… ¡integrara los fotones! (que son sensibles a la gravedad). Y la escala de las partículas M “medio” deberían ser del orden del llamado “vacio cuántico”.
¿A nivel microscópico… esto es mecánicamente posible? ¿puede ocurrir en los fluidos?