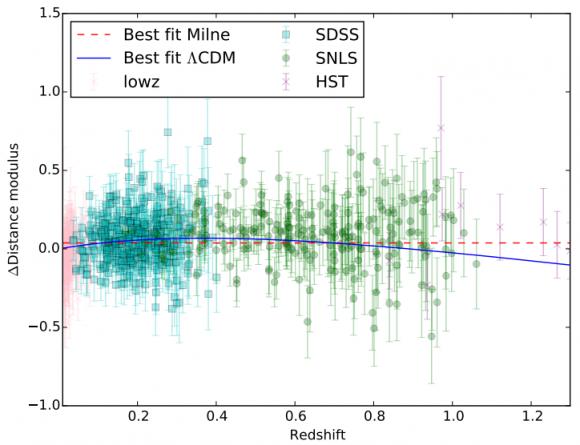
El grupo de Perlmutter, Premio Nobel de Física, descubrió la expansión cósmica acelerada tras analizar 42 supernovas de tipo Ia (catálogo JLA); su resultado fue que Λ>0 al 99% de confianza estadística. En su tesis doctoral, Jeppe Trøst Nielsen ha repetido su análisis con el nuevo catálogo JLA, que cuenta con 740 supernovas Ia, y ha confirmado a casi tres sigmas que Λ>0, es decir, a casi el 99,7% C.L. Como tres sigmas es menos de cinco sigmas afirma que la evidencia de la aceleración cósmica es marginal. La razón es que sus directores de tesis, Subir Sarkar y Alberto Guffanti, son conocidos opositores a la idea de la energía oscura.
Has leído bien. Han obtenido una mayor confianza estadística que la lograda en el artículo que le dio el Nobel a Perlmutter. Pero la interpretan en el sentido opuesto. Más aún, algunos blogueros, como Anthony Watts, afirman que estos indicios a 3 sigmas indican que el Nobel fue concedido sin una evidencia firme. Como comprenderás, cuando se concedió el Nobel en 2011 había evidencias fuertes (a mucho más de cinco sigmas) de la aceleración cósmica. Repetir en 2015 un análisis de 1998 y olvidar todas las evidencias entre 1998 y 2011 no parece una buena praxis científica. Más aún cuando hoy en día se conocen más de 8000 supernovas Ia (Open Supernova Catalog).
El artículo es J. T. Nielsen, A. Guffanti, S. Sarkar, «Marginal evidence for cosmic acceleration from Type Ia supernovae,» Scientific Reports 6: 35596 (03 Oct 2016), doi: 10.1038/srep35596, arXiv:1506.01354 [astro-ph.CO]; la tesis doctoral con más detalles es Jeppe Trost Nielsen, «Supernovae as cosmological probes,» arXiv:1508.07850 [astro-ph.CO].
Mete ruido sobre el tema Anthony Watts, «‘Settled Science’ syndrome hits Astronomy and the Nobel Prize,» WUWT, 21 Oct 2016; no soy el único que se escandaliza por su sesgo, también Luboš Motl, «Dark energy and unsettled science,» TRF, 23 Oct 2016.
[PS] En la línea de ensalzar el resultado de Sarkar puedes leer «Físicos de Oxford cuestionan que el Universo se expanda aceleradamente,» Europa Press, 24 Oct 2016.
Motl destaca esta figura que muestra como la evidencia actual de la energía oscura debida a supernovas Ia (elipses azules) es la menos significativa de todas las evidencias disponibles, como los cúmulos galácticos (elipses verdes) y el fondo cósmico de microondas (elipses naranjas). La confianza estadística actual sobre la energía oscura queda ilustrada por el círculo rojo (combinación de todas las evidencias) que es mucho mayor de cinco sigmas (la elipse azul oscuro es la evidencia a tres sigmas debida a las supernovas Ia).
¿Por qué Perlmutter, Schmidt y Riess recibieron el Premio Nobel de Física 2011? Por el descubrimiento de la aceleración de la expansión del universo en 1998 (más tarde llamada energía oscura). Si sus indicios hubieran alcanzado cinco sigmas en aquella época habrían recibido el Premio Nobel sobre el año 2000. Pero lo recibieron en 2011 porque fue necesaria una década para alcanzar la evidencia definitiva. Dudar ahora es dudar por dudar. Meter ruido entre los aficionados a la divulgación científica.



«La razón es que sus directores de tesis, Subir Sarkar y Alberto Guffanti, son conocidos opositores a la idea de la energía oscura.»
Visto desde fuera el sesgo se aprecia por doquier.
Mm, yo tenía entendido que lo de las 5 sigmas es para física de partículas o en general muestras que incluyan millones de mediciones, porque en una muestra tan grande pequeñas fluctuaciones estadísticas te pueden dar un falso positivo con gran facilidad.
En una muestra de 42 estrellas, 2 sigma es suficiente para evitar el error de tipo I, pero si sumamos que además como dices se ha obtenido evidencia con mucha más significancia, esto no tiene ni pies ni cabeza.
Yeil, como bien comentas la gran diferencia entre física de partículas y cosmología es la estadística, muy pobre en el segundo caso. Pero para mucha gente las cinco sigmas se usan en todas las ramas de la física fundamental (recuerda el caso de los modos B de BICEP2, por ejemplo).
¿Cuantas supernovas hay que observar para que tengamos una confianza estadística de 5 sigmas?
Luis, ni idea. Se conocen al menos dos tipos de supernovas Ia y no sabemos diferenciarlas con facilidad. Por ello las estimaciones de distancias usando estas supernovas tienen un error sistemático alto, que impide que sólo con estadística (mayor número) se reduzca el error total y con él crezca el número de sigmas. Se necesitan importantes avances en nuestra comprensión de las supernovas Ia para lograr alcanzar cinco sigmas.
Depende del tamaño del efecto que se esté observando. Yo he obtenido más de 5 sigma con muestras de solo 14 pacientes, pero porque el efecto que estaba midiendo era muy grande.
El tamaño del efecto se calcula mediante la diferencia de medias y homogenización de desviaciones estándar, como describió Cohen.
Supongo, Yeil, que con 14 pacientes habrás calculado el intervalo de confianza usando la distribución t de Student (en otro caso lo habrás hecho mal). Lo digo porque quizás olvidas que el tamaño del efecto no influye, ni importa.
Utilicé el estadístico U, cuya distribución en muestras grandes se asemeja a la normal, pero en muestras pequeñas no presupone una distribución sino que trabaja de forma discreta, por rangos. Bueno, realmente trabaja por rangos también en muestras grandes, pero ahí se asemeja a una normal y ya no tiene mucho sentido utilizar este estadístico.
Discrepo en que el tamaño del efecto no influye ni importa, con un tamaño del efecto como el que es habitual en mi rama (0,1-0,7 mm) jamás hubiese detectado diferencias con tan solo 14 pacientes, y mucho menos a 5 sigma. Lo que pasa es que este estudio analizaba tiempos entre dos técnicas en la que una tarda 14 minutos y la otra 28, con una desviación estándar de 1 min. Con un tamaño del efecto tan grande es posible conseguir gran significancia con muestras minúsculas. Por cierto que lo he revisado y eran 18 pacientes, pero para el caso es casi lo mismo.
Tengo curiosidad, ¿por qué dices que el tamaño del efecto no influye ni importa? Si estás buscando diferencias claro que será más fácil encontrarlas cuanto más grandes sean, y más difícil será que se deban al azar.
Un saludo
De hecho para el cálculo muestral lo que se utiliza son cuatro valores, alpha (equivalente a la significancia estadística que quieres tener), beta (máximo error tipo II asumible), desviación estándar combinada entre ambos grupos y diferencia entre ambos grupos. Con los dos últimos se calcula el tamaño del efecto.
Cuanto más parecidos son ambos grupos, más muestra necesitas para encontrar diferencias, para que el error aleatorio no oculte esas diferencias.
En el caso de BICEPs imagino que la muestra sería de millones de datos también.
Aumentar la muestra no sale gratis, disminuye el error de tipo II, pero aumenta el de tipo I. Un ejemplo de típico de mala ciencia es hacer un cálculo del tamaño muestral y quedarte al borde de la significancia, dices, pues meto 50 pacientes más y mágicamente ya es significativo. Publico en revista de alto impacto y a los pocos años salen un montón de trabajos que contradicen mis resultados ¿qué ha pasado? Pues que el cálculo del tamaño muestral se hace por muchos motivos pero uno es adecuar el tamaño de la muestra a la significancia que buscas, si introduces más gente tienes que aumentar las sigma para que sea correcto, pues al reducir los errores estándar una simple fluctuación estadística te puede salir fácilmente como significativa, lo cual es raro que ocurra con muestras pequeñas.
Del mismo modo pedir más sigma disminuye el error de tipo I pero aumenta el de tipo II, lo cual puede llevar a que efectos donde es imposible obtener una muestra grande no los detectemos no por la sensibilidad de nuestros sensores, sino por la forma con la que estamos tratando la estadística.
Vamos, que no considero que la de la cosmología u otras ramas de la física sea pobre, sino adaptada a su muestra.
Un saludo.
Yeil, el contraste de hipótesis en el caso de BICEP2 se obtuvo para la hipótesis r>0 respecto a la hipótesis nula r=0; se obtuvo r=0,20 +0,07 -0,05 usando 5 bins de datos y se afirmó que eran 7 sigmas; dicho cálculo fue muy criticado por los expertos en estadística.
Buenas. Pues no tengo muy buena memoria, pensaba que la crítica venía no por la estadística, sino porque el polvo que se presuponía en esa zona era mucho menor al real, por lo tanto como si hubiesen sido 10 sigma, seguiría siendo inválido, porque han utilizado un modelo incorrecto al contrastar.
Buscaré la parte de la estadística a ver.
Yeil, por supuesto, los modos B observados supuestamente cosmológicos eran espurios, debidos a la radiación polarizada del polvo. Pero el artículo original suponía que no había polvo en la ventana de BICEP2; bajo dicha suposición, realizaba un contraste de la hipótesis de que fueran modos B cosmológicos con la hipótesis nula de que fuesen modos B espurios debidos al efecto lente gravitacional sobre los modos E; dicho análisis también fue criticado por los expertos en estadística (que es a lo que yo me refería más arriba).
Por lo que he visto hay otras evidencias observacionales a favor de que la energía oscura existe, no solo las supernovas de tipo Ia. Que debido a que hay dos tipos de ellas nos hayamos equivocado y el Universo no se esté expandiendo tan aceleradamente no sería tan extraño.
Ese fue el Nobel que le ROBARON a 2 astrónomos Chilenos, Hamuy y Maza, cuando Riess y el otro, los estafaron con los datos obtenidos por los chilenos y publicaron ANTES que ellos un estudio sobre la expansión acelerada que los chilenos ya habían descubierto, lo que habían conversado. Los ladrones del Nobel pidieron prestado esos datos, pero confabularon para publicar sin permiso.
Ladrones de Nobel.
http://www.lanacion.cl/mario-hamuy-y-el-premio-nobel-de-fisica-2011-hubo-una-falta-a-la-etica/noticias/2011-10-05/183407.html
http://diario.latercera.com/2011/07/24/01/contenido/tendencias/16-77632-9-la-historia-desconocida-del-hallazgo-cientifico-que-enfrento-a-astronomos.shtml
http://www.otrocanal.cl/video/jos-maza-y-mario-hamuy-un-viaje-al-corazn-del-csmos
¿Los medios Chilenos que van a decir? Barren para casa como hacen todos.
No lo entiendo. ¿Como teniendo una certeza mayor puedes interpretarlo al contrario?
¿Acaso están sugiriendo que Perlmutter interpretó los datos mal?
Álvaro, olvidan las evidencias y discuten los indicios como si no existieran las evidencias. Un sesgo de libro.
Anthony Watts, el hombre del tiempo que quería reinventar la climatología y ahora parece que se atreve con la cosmología 🙂 Lo irónico del caso es que la misma crítica que hace Lubos a Watts se aplica todo el tiempo a su tratamiento sesgado de la climatología, de la que tampoco tiene la más remota idea. Pero Lubos, bastante cerca del negacionismo por cierto (aunque en su caso parece más bien un ejemplo del efecto Dunning-Kruger,) , no tiene problemas en considerarlo un blog valioso en una disciplina en la que Lubos no es capaz de detectar justo el mismo tipo de proceder o_O
Me gustaría que alguien me aclarase un par de puntos, si es posible, y que conste que no estoy entrando en ninguna polémica. Está claro que todo el mundo, en cuanto individuos, tenemos sesgos y motivaciones, espurias, bastardas o altruistas (o hasta las tres cosas a la vez, no son incompatibles), pero una cosa es explorar dudas razonables a ver qué hay y otra remover mierda simplemente para que huela. Por eso pregunto, porque el cuadro no lo tengo claro (y una vez más, podrían ser ambas cosas).
-Hasta donde sé, para supernovas bastante lejanas (más de 5 millardos de años-luz) se *debe* medir que no había expansión acelerada, es lo predicho, sin embargo esto no ha podido ser establecido (aún). No me es posible encontrar información al respecto que me dé una respuesta satisfactoria, ¿exactamente cuál es la causa de que esto no se pueda comprobar (o descartar, todavía)? No me parece que la distancia sea precisamente el problema.
-Por otro lado las Ia tienen subtipos y no son candelas perfectas, ni mucho menos. ¿Estamos seguros del grado en que esto afecta nuestras medidas (o al menos del sesgo que se podría estar introduciendo)?
Leído hoy:
«IS THE EXPANSION OF THE UNIVERSE ACCELERATING? ALL SIGNS POINT TO YES.
A recent study (Trøst Nielsen et al. 2015) has claimed that the evidence for acceleration from SNe Ia is “marginal.” Here we demonstrate errors in that analysis … »
https://arxiv.org/abs/1610.08972
Saludos.
Hoy he visto otro artículo que «se carga» las conclusiones de Nielsen- Guffanti- Sarkar, es “Strong evidence for an accelerating Universe” y este es el enlace:
https://arxiv.org/pdf/1702.08244.pdf
Saludos.
También, David Rubin, Brian Hayden, «Is the expansion of the universe accelerating? All signs point to yes,» ApJ 833: L30 (2016), doi: 10.3847/2041-8213/833/2/L30, arXiv:1610.08972 [astro-ph.CO], y Isaac Tutusaus, Brahim Lamine, …, Alain Blanchard, «Is cosmic acceleration proven by local cosmological probes?» A&A 602: A73 (2017), doi: 10.1051/0004-6361/201630289, arXiv:1706.05036 [astro-ph.CO], entre otros.
Yo no preocuparía demasiado. Al final conoceremos la verdad, sea cual sea. Esto ha ocurrido siempre en la Ciencia, en todos los campos, y lo que no se acepta hoy se acepta mañana. Y dada la velocidad a la que se hacen nuevos descubrimientos no creo que tarde mucho en saberse.
Estube leyendo sobre el caso del astronomo chileno y me recordo al de mi profesor https://es.wikipedia.org/wiki/Julio_%C3%81ngel_Fern%C3%A1ndez el es quien propuso lo que ahora se conoce como la nube de Oort unos 4 años antes que el antedicho Jan Oort.
El en su admirable modestia docente lo citaba como si nada, al pasar. sin hacer escandalos en la prensa ni busqueda de (muy merecida por cierto) notoriedad.
Bueno saludos desde el exilio socioeconomico a todos los compañeros que por ahi podrian estar leyendo este excelente blog
Perdona, zxdfgh, no entiendo: Jan Oort propuso la nube de Oort en 1950 para resolver un problema con los cometas de 1932. Juan Ángel Fernández nació en 1946.
Me deja perpleja el comentario de «Meter ruido entre los aficionados a la divulgación científica». Bueno, con todas las disculpas, entiendo que la divulgación científica viene después en orden de importancia. Con todos los sesgos y lo que quieras me imagino que la discusión importante se da en el sector profesional, no creo que les preocupe mucho lo que pasa a nivel divulgativo, ni tiene por qué preocuparles en primera instancia. Primero sustentar el conocimiento, luego darlo a conocer.
Hoy he visto que Sarkar y cia. han publicado en Astronomy & Astrophysics otro artículo negacionista de la expansión acelerada del universo, «Evidence for anisotropy of cosmic acceleration»
https://www.aanda.org/articles/aa/abs/2019/11/aa36373-19/aa36373-19.html
Saludos.
Albert, el artículo apareció en arXiv en agosto de 2018: https://arxiv.org/abs/1808.04597 Este tipo de artículos en los que, o bien sus autores tienen razón y todos los demás están equivocados, o bien sus autores están equivocados y todos los demás tienen razón, siempre nos llevan al mismo sitio: la segunda opción. La razón es que su propuesta no explica todo lo que sabemos, como sí lo hace el modelo cosmológico de consenso. Así que hasta que no logren explicar lo que ya sabemos explicar, sus propuestas negacionistas son solo especulaciones sin ningún eco relevante en la comunidad científica.
Si te interesa el tema, te recomiendo leer a Matthew von Hippel, «When to Trust the Contrarians,» 4 gravitons, 25 Oct 2019, y la respuesta de Mohamed Rameez, «Guest Post: On the Real Inhomogeneous Universe and the Weirdness of ‘Dark Energy’,» 4 gravitons, 15 Nov 2019.
Muchas gracias por responder y por los enlaces, saludos.