Un fotón se mueve en el vacío a la velocidad de la luz en el vacío. Un grupo de fotones puede viajar en el vacío a una velocidad de grupo menor que la velocidad de la luz en el vacío. Basta que tenga estructura espacial transversal de tamaño finito, como publican en Science el físico Miles J. Padgett (Univ. Glasgow, Escocia) y varios colegas. Lo demuestran usando haces de Bessel y haces gaussianos enfocados.
La velocidad de grupo de un solo fotón no tiene sentido físico, pues está descrito por una onda plana, cuya estructura espacial transversal es infinita (aunque muchos físicos afirman a la ligera que coincide con la velocidad de fase en este caso). Para determinar la velocidad de un grupo de fotones que presentan una correlación espacial transversal hay que detectar, al menos, una pareja de fotones. En el detector estos dos fotones no se observan de forma simultánea, con lo que la velocidad de grupo es menor de la velocidad en el vacío de cada uno de estos fotones. En el experimento de Padgett y sus colegas se observan parejas de fotones en el mismo haz separados varias micrómetros en una distancia total de propagación de un metro.
Un artículo muy interesante que te recomiendo Daniel Giovannini et al., «Spatially structured photons that travel in free space slower than the speed of light,» Science, AOP 22 Jan 2015; arXiv:1411.3987 [physics.optics].
Un haz de Bessel es un campo electromagnético cuya amplitud radial transversal se describe por una función de Bessel J(r). Durante muchos años se pensó que era imposible crear un haz de Bessel en laboratorio. En teoría su formación requiere una energía infinita. Pero en el año 2012 se demostró que en teoría se podían obtener en laboratorio usando una energía finita (se puede crear algo que se parece tanto a un haz de Bessel teórico que recibe dicho nombre) y en el año 2013 se fabricaron de forma experimental por primera vez. Hoy en día estos haces (no sólo ópticos, también acústicos) se usan mucho en la manipulación óptica de objetos microscópicos, por ejemplo, células vivas. Los artículos originales fueron Ioannis Chremmos et al., «Bessel-like optical beams with arbitrary trajectories,» Optics Letters 37: 5003-5005, 2012, y Zhao Juanying et al., «Observation of self-accelerating Bessel-like optical beams along arbitrary trajectories,» Optics Letters 38: 498-500, 2013.
Para las personas que hablan a la ligera de la luz y del concepto de velocidad de la luz, el nuevo trabajo publicado en Science puede resultarles paradójico. Mucha gente olvida que la velocidad de luz en un medio puede ser menor que la velocidad de la luz en el vacío, la velocidad de los fotones individuales. Y también olvidan fácilmente que la velocidad de un pulso de luz, o de un haz de luz, incluso en el vacío (en el espacio libre), puede ser menor que la velocidad de un fotón individual. El cálculo matemático es sencillo y cualquier físico puede realizarlo sin problemas. Pero poner palabras a los cálculos matemáticos no siempre es fácil y muchas veces se olvidan los adjetivos que requiere una descripción rigurosa de los conceptos físicos usados. Resulta pesado repetir los adjetivos una y otra vez, por lo que muchos expertos los omiten; el contexto determina de forma unívoca estos adjetivos y el experto logra la brevedad que exige un artículo científico. Pero los legos caen en la trampa, sobre todo cuando extraen fuera de su contexto frases literales de dichos artículos.
Y no sólo los legos se confunden, también muchos físicos que no han estudiado en su carrera los haces de luz con estructura espacial transversal. Muchos físicos estudian la diferencia entre velocidad de fase, velocidad de grupo, velocidad de la energía, velocidad de la señal, etc., en haces de luz confinados en guías ópticas. En estos medios con índice de refracción mayor de la unidad (el del vacío) es muy fácil entender estos conceptos. Sin embargo, quienes trabajan en óptica física y quienes trabajamos en propagación de ondas sabemos que estas diferentes velocidades también se aplican a los haces de luz con estructura espacial transversal en el espacio vacío. Ello no quita mérito al nuevo trabajo experimental. Forzar en laboratorio que la diferencia entre estas velocidades para un haz de Bessel sea medible no es fácil y requiere un esquema experimental adecuado. Por ello este nuevo trabajo se ha publicado en una revista tan prestigiosa como Science, en lugar de Optics Letters o Physical Review Letters, por ejemplo.
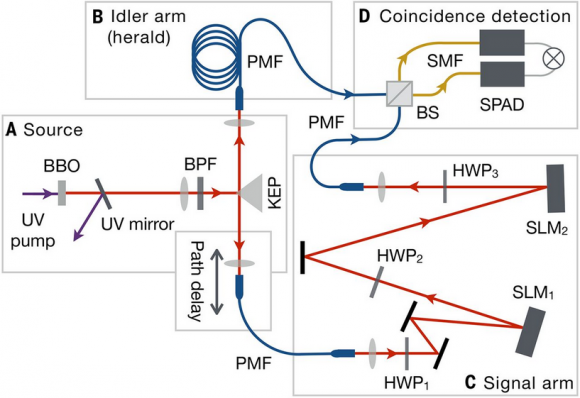
Para producir un haz de Bessel se puede usar una lente cónica (axicon) o un prisma de hoja de cuchillo (knife-edge prism, KEP en la figura del esquema experimental). La velocidad de grupo de un haz de Bessel se reduce en una cantidad finita que depende de la apertura del sistema óptico (el parámetro se llama α, remito al artículo original para su definición precisa). Este retraso puede ser muy superior a muchas longitudes de onda óptica y, en teoría, puede ser medido en el vacío (espacio libre). Normalmente esta diferencia se mide en haces de luz clásicos (con una cantidad de fotones tan grande que no es posible contar fotones individuales).
El nuevo trabajo presenta un esquema experimental que permite medir esta diferencia con haces cuánticos formados por un número finito, pequeño, de fotones; de hecho, con el mínimo posible, una pareja de fotones. La diferencia es muy pequeña (un retraso en tiempo de 30 femtosegundos en una distancia total de un metro, que equivale a una separación en el espacio de 10 micrómetros). Como es obvio para todo el mundo, medir intervalos de tiempo en el régimen de los femtosegundos no es moco de pavo. El nuevo trabajo usa un efecto cuántico llamado interferencia HOM por Hong–Ou–Mandel (C. K. Hong, Z. Y. Ou, L. Mandel, «Measurement of subpicosecond time intervals between two photons by interference,» Phys. Rev. Lett. 59: 2044-2046, 1987). No quiero entrar en detalles técnicos, sólo indicar que se usan parejas de fotones entrelazados obtenidos mediante conversión paramétrica hacia abajo, uno de los cuales se retrasa mediante su propagación en una fibra óptica.
Para determinar la velocidad de grupo del haz de Bessel es necesario detectar al menos dos fotones (un fotón de señal y su fotón gemelo o acompañante, en inglés signal & idler photons). Ambos fotones de 710 nm se producen en el mismo instante, pero llegan al detector con un desfase en tiempo. Para ello el fotón de señal se propaga en el vacío (espacio libre), pero el fotón gemelo se propaga a través de una fibra óptica que conserva la polarización. Gracias a la interferencia cuántica de HOM el efecto de la fibra se puede descontar y el resultado final de la medida es el mismo que si se hubiera obtenido propagando en el espacio libre ambos fotones en un haz de Bessel.
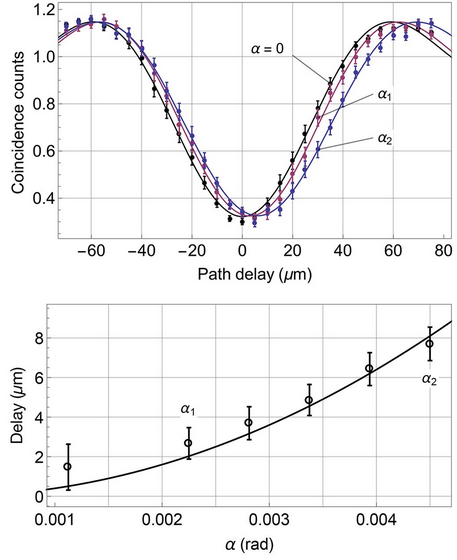
El diseño experimental permite comparar el resultado para un haz de Bessel y para un haz plano. El retraso medido para una distancia de propagación de un metro corresponde a una distancia de 2,7±0,8 µm para un haz de Bessel con reducción teórica de la velocidad de grupo de α=0,00225 radianes (en teoría debería dar 2,0 µm) y de 7,7±0,8 µm para α=0,00450 rad (que en teoría debería dar 8,1 µm). El buen acuerdo entre teoría y experimento es una clara señal de que se están usando haces de Bessel «en el vacío» aunque se usen parejas de fotones (uno de los cuales se retrasa mediante una fibra óptica).
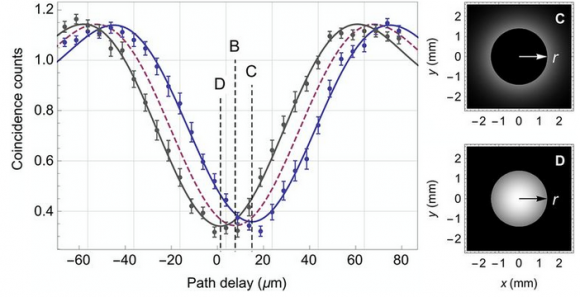 Por supuesto, el efecto se observa para cualquier haz de luz con estructura espacial transversal. Los autores de este trabajo lo ilustran usando haces gaussianos (mostrados en esta figura). Para una distancia de propagación de 40 cm, cuando se tapa el haz con un círculo de 1,4 mm de radio (inciso C en la figura) se obtiene un retraso adicional de 7,3±0,4 µm, resultando un retraso total de 15,0±0,6 µm; cuando se pasa el haz por una apertura circular del mismo radio (inciso D en la figura), se reduce el retraso en 6,4±0,4 µm, resultando un retraso total de 1,3±0,6 µm. Estos resultados están en buen acuerdo con las predicciones teóricas, de nuevo, una indicación clara de que se han propagado dos fotones en un haz gaussiano.
Por supuesto, el efecto se observa para cualquier haz de luz con estructura espacial transversal. Los autores de este trabajo lo ilustran usando haces gaussianos (mostrados en esta figura). Para una distancia de propagación de 40 cm, cuando se tapa el haz con un círculo de 1,4 mm de radio (inciso C en la figura) se obtiene un retraso adicional de 7,3±0,4 µm, resultando un retraso total de 15,0±0,6 µm; cuando se pasa el haz por una apertura circular del mismo radio (inciso D en la figura), se reduce el retraso en 6,4±0,4 µm, resultando un retraso total de 1,3±0,6 µm. Estos resultados están en buen acuerdo con las predicciones teóricas, de nuevo, una indicación clara de que se han propagado dos fotones en un haz gaussiano.
En resumen, si te dicen que el nuevo trabajo demuestra que un fotón en el vacío se mueve a una velocidad inferior a la velocidad de la luz en el vacío te están engañando. Te deben decir que se ha demostrado que parejas de fotones en un haz de Bessel o en un haz gaussiano se mueven en el vacío con una velocidad de grupo menor que la velocidad de la luz en el vacío. La diferencia parece sutil pues depende de los adjetivos usados. Pero en este caso, como en todos los casos, los adjetivos son imprescindibles.



No acabo de estar de acuerdo con la siguiente frase:
«La velocidad de grupo de un solo fotón no tiene sentido físico, pues está descrito por una onda plana, cuya estructura espacial transversal es infinita»
Según lo veo yo un fotón no tiene por qué estar descrito por una onda plana; uno podría definir un estado de campo (por ejemplo, del continuo de modos en una guía de onda 1D) como una combinación de estados de un fotón con distinta longitud de onda. La velocidad de grupo sería la velocidad de la luz en el vacío si la relación de dispersión no ha sido modificada por la guía (que sí lo es), pero eso no significa que no tenga sentido físico.
Al menos así lo entiendo yo…
[COMPACTADO por Francis]
Un fotón es una excitación elemental del campo electromagnético. Si un qubit excitado decae emitiendo a una guía de ondas (por seguir con el ejemplo), el campo en el estado final contiene con total seguridad una única excitación, pero que tiene un perfil temporal, y por tanto también un perfil en frecuencias. Creo que en un contexto científico muy amplio se considera que lo que hay en esa guía es un fotón.
[COMPACTADO por Francis]
Quiero saber si es solo lenguaje o hay alguna sutileza física ¿Cual sería la diferencia con un electrón que está en una combinación de dos estados con momento diferente? ¿También ahí dirías que hay más de un electrón? Si dices que una onda está formada por más de un fotón, ¿no quiere decir eso que la probabilidad de detectar más de un fotón es distinta de cero? ¿Cómo puede ser así en un estado del tipo |phi>=|k1>+|k2>, que solo contiene una excitación?
Carlos, he compactado tus tres comentarios en uno, porque ahora creo que entiendo tu duda.
(1) Un sistema cuántico con estados discretos (en energía, espín, o lo que sea) puede estar en un estado de superposición. Por ejemplo, un átomo tiene un conjunto discreto de estados energéticos (sus electrones pueden ocupar diferentes niveles de energía). Por ello un átomo (a veces se abusa del lenguaje y se dice «un electrón en un átomo») puede estar en un estado de superposición, sea |phi>=|k1>+|k2>, donde |k1> y |k2> representen dos niveles energéticos para el electrón en el átomo.
(2) Un fotón y un electrón son partículas elementales (o fundamentales), a diferencia de un átomo que es un sistema compuesto. La frecuencia (o la energía) de un fotón es una magnitud continua; no es una magnitud discreta; por ello un fotón no puede estar en un estado de superposición en frecuencia (creo que te confundes en este punto). Un electrón tiene una energía (o un momento) que también es una magnitud continua; no es discreta si el electrón está libre, sólo puede ser discreta dentro de un sistema (átomo, pozo de potencial, etc.); por ello un electrón libre no puede estar en un estado de superposición en energía (o momento).
(3) Una onda electromagnética en una guía de ondas puede tener estados discretos en la dirección transversal (los modos guiados). Un único fotón no puede tener estados de este tipo en una guía (no se puede confinar un fotón, pues implica localizarlo en espacio y la física cuántica lo prohíbe). Creo que aquí está tu confusión. Se requieren muchos fotones para poder hablar de modos discretos confinados en una guía. No te confundas, no son estados de superposición cuánticos de un único fotón. Una onda electromagnética con estructura temporal o con estructura espectral tiene varias frecuencias, y por tanto tiene muchos fotones. Un fotón sólo puede tener una frecuencia.
Espero haber aclarado tus dudas. Cualquier texto de mecánica cuántica te permitirá profundizar y te aclarará estos conceptos, que son muy básicos. Si te interesa el tema, estudia, es más fácil de lo que parece.
Saludos
Francis
Francis, gracias por dedicarle tiempo a la respuesta, siento inundarte el blog de comentarios.
Antes me preguntaste por mi formación; he estudiado Física, así que los libros de cuántica básica me los tengo leídos (aunque nunca viene mal repasarlos, oye). De todos modos, aunque mi comentario te haya parecido tan fundamentalmente erróneo, algunas cosas de tu respuesta me siguen pareciendo muy extrañas, así que con tu permiso voy a correr el riesgo de quedar como un zoquete y voy a responder.
No recuerdo haber estudiado nunca que un sistema debe de ser discreto para que se aplique el principio de superposición, la única diferencia es pasar de una base discreta a una continua. Lo que sí recuerdo haber estudiado es la evolución de una partícula libre (como podría ser un electrón) con una función de onda Gaussiana, que no es otra cosa que una superposición de distintas energías. Me choca muchísimo que digas que esto no puede ser así por el mero hecho de ser un sistema continuo…
También me choca que digas que no se puede confinar un fotón porque la física cuántica lo prohíbe… Obviamente hay un límite que vendrá dado por el principio de incertidumbre, pero en las microcavidades ópticas (como por ejemplo, los defectos en un cristal fotónico) está a la orden del día confinar los fotones discretizando los modos en las tres direcciones, y no hay nada fundamental que te impida trabajar con estados de Fock de un solo fotón en uno de estos estados confinados. De modo que tampoco entiendo tu comentario de que se necesitan muchos fotones para hablar de un modo discreto confinado…
Carlos, debes empezar por ahí, diciendo que eres físico, para que yo sepa que lenguaje puedo usar. No es lo mismo un chaval de 14 años, que un filólogo de 30 años, que un licenciado en físicas.
Como bien sabrás no existe un operador de posición autoadjunto en el espacio de estados de un fotón; tampoco existe ninguno en el espacio de Fock para un electrón; de hecho, no existe para ninguna partícula en ninguna teoría cuántica de campos que cumpla la axiomática de Wightman. Por tanto un fotón no es localizable como tampoco lo es un electrón libre.
Otra cosa muy diferente es usar una aproximación no relativista para un fotón o un electrón mediante una función de onda gaussiana, para lo que existe un operador de posición autoadjunto trivial. Como bien sabrás en teoría cuántica de campos el concepto de función de onda no tiene sentido físico. No es observable ni medible. La teoría cuántica relativista tiene estas cosas.
En un curso de mecánica cuántica no relativista se abusa de los conceptos físicos y se describe un «fotón» (o un «electrón libre») por una función de onda cuántica no relativista; por supesto esta descripción de carácter académico no describe un fotón físico (ni un electrón físico). Se trata de una aproximación matemática para resolver problemas de forma aproximada sin ninguna validez conceptual (aunque una gran validez docente porque permite atacar ciertos problemas con herramientas matemáticas de un primer curso de física cuántica).
Un «electrón libre» se puede localizar (en mecánica cuántica no relativista) en una región con un tamaño de su longitud de Compton, el inverso de su masa. Con un «fotón libre» no se puede hacer porque la masa es nula y por tanto la longitud de Compton es infinita. Sin embargo, para un «fotón» dentro de una guía de ondas se puede definir una masa efectiva (dada por la frecuencia de corte como frecuencia de Compton) y se puede localizar dicho «fotón» en una región con un tamaño dado por su longitud de Compton efectiva. Este proceso de localización no relativista conduce a que el «fotón» se encuentre descrito por un único modo guiado. Haz los cálculos como ejercicio y compruébalo, es más fácil de lo que parece. No es posible que el «fotón» se encuentre en una superposición cuántica de estados asociados a diferentes modos en la guía. El cálculo no relavitista es sencillo, te animo a hacerlo. Si eres un poco vago, recurre a ArXiv (te he dado las palabras clave y te será fácil buscar papers que discuten este asunto con todos los detalles).
Por último, nota que a veces uso «fotón» y a veces uso fotón. No es por gusto.
Saludos
Francis
Gracias por la respuesta tan detallada, Francis, es muy interesante.
Soy físico, pero dos físicos pueden acabar la carrera con formaciones muy distintas, y en mi caso la cuántica de campos la vi muy tangencialmente, por lo que sus conceptos no me resultan tan básicos.. Veo que ahí estaba el problema, ya que mi concepción de la cuántica de todos los días es puramente no relativista. De todos modos, sigo sin entender que en cuántica de campos no puedas construir un estado fotónico del tipo (a*_k1 + a*_k2)|0> , pero sabiendo que van por ahí los tiros puedo seguir tu consejo y mirarlo. Sin embargo, en la bibliografía de óptica cuántica, este tipo de estados aparecen continuamente.
Una última pregunta, ¿cómo interpretas entonces un «fotón» en término de fotones en el formalismo relativista?
Gracias, Francis. Un saludo.
Carlos, tu última pregunta no tiene respuesta de consenso. No sabemos qué es un «fotón» en términos de fotones y vacío del campo; el problema es que el vacío fluctúa y no sabemos su estado, pero polariza a los fotones. Hay cientos de artículos que discuten esta cuestión. Como siempre la palabra «interpretación» lleva a opiniones diversas a las que se llama interpretaciones. No sabemos interpretar un campo electromagnético clásico en término de fotones y vacío en QED; tampoco un «fotón» en óptica cuántica.
Recuerda que qué es un fotón es uno de los problemas aún sin resolver de la física del siglo XX; la razón es que un fotón es un estado físico sobre un estado de vacío y este último no sabemos describirlo con palabras (los abusos de términos como «fotones virtuales» lleva a muchos maltendidos). No podemos explorar con experimentos el vacío en detalle y por tanto tan poco un fotón individual.
Por ello no se conoce la relación que existe entre el mal llamado formalismo de segunda cuantización que se usa en óptica cuántica para describir «fotones» y el que se usa en QED para describir fotones. Existen los campos EM cuánticos y podemos observarlos como vacío y como fotones; en la interacción cuántica entre la luz y la materia se usa el concepto de «fotones» porque a día de hoy no sabemos usar el concepto de fotones (que sólo podemos explorar en interacciones partícula-partícula, pero no en interacciones átomo-partícula o medio-«fotón»).
Como supongo que no te satisface mi respuesta, te hago unas recomendaciones para leer (si tienes tiempo y te interesa el tema): Se leen fácil los artícuos del número «What is a photon» de Optics & Photonics News, OSA, 2003; en especial te recomiendo el artículo de los expertos en óptica cuántica Scully y Zubairy, pp. 17-27 (su libro «Quantum Optics,» CUP (1997), lo discute en las pp. 20-40).
Si quieres mi opinión personal, a mi me gusta la idea de interpretar un «fotón» como lo descrito por la «función de onda de un fotón» introducida por Bialynicki-Birula (p.ej. Progress in Optics, 1996); pero no pondría en la mano en el fuego, pues tras leer cientos de artículos (hace tiempo traté de escribir un artículo de revisión para Am. J. Phys. sobre el tema), hay matices en el uso del concepto «fotón» por diferentes autores que no refleja bien las ideas de Bialynicki-Birula.
Saludos
Francis
¡Qué interesante! No sabía que existía este gap conceptual entre el fotón de QED y el «fotón» de óptica cuántica, el cual para mí era el fotón (sin comillas). Muchas gracias por todo este material para leer . ¡Un saludo!
Me he leído algunos de los artículos del número «What is a photon» que me recomendaste (incluyendo el de Scully) y por desgracia no he visto claro que en ninguno se discuta la diferencia entre el fotón de óptica cuántica y el de QED. De hecho, en todos se trata el fotón en el formalismo que yo conozco (óptica cuántica), e incluso se habla del «single photon wavepacket» en términos de la superposición que yo comentaba en mi primer post (ecuación 7, página 10). Intentaré ponerme con algún libro de cuántica de campos, que el tema me interesa mucho.