El 4 de enero de 2018 se publicaron en Nature dos artículos que presentan análogos físicos 2D del efecto Hall cuántico entero en 4D. Algunos medios han aprovechado para titular cosas como que «observan en laboratorio el reflejo de una cuarta dimensión espacial. [El] reflejo en 3D de un objeto 4D, un descubrimiento que puede revolucionar los fundamentos básicos de la ciencia actual» [T21, 11 Ene 2018]. Varios seguidores de este blog me habéis pedido una explicación para legos, que evite posibles malentendidos. ¿Realmente se ha observado por primera vez un objeto en cuatro dimensiones? No, lo siento, se han estudiado sistemas 2D que muestran comportamientos que se parecen (pero no son idénticos) al de cierto sistema 4D, nada más y nada menos.
Los artículos son Michael Lohse, Christian Schweizer, …, Immanuel Bloch, «Exploring 4D quantum Hall physics with a 2D topological charge pump,» Nature 553: 55–58 (04 Jan 2018), doi: 10.1038/nature25000, arXiv:1705.08371 [cond-mat.quant-gas], y Oded Zilberberg, Sheng Huang, …, Mikael C. Rechtsman, «Photonic topological boundary pumping as a probe of 4D quantum Hall physics,» Nature 553: 59–62 (04 Jan 2018), doi: 10.1038/nature25011, arXiv:1705.08361 [quant-ph].
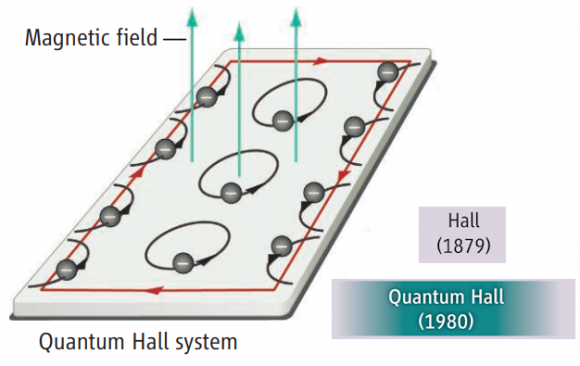
El efecto Hall cuántico entero (1980), análogo cuántico del efecto Hall clásico (1879), recibió el Nobel de Física en 1985. En un material metálico 2D, a baja temperatura, la conductividad eléctrica se discretiza al aplicar un intenso campo magnético transversal. Como ilustra la figura, los electrones en dos dimensiones siguen órbitas de tipo ciclotrón debido al campo magnético; en los bordes del material se propagan corrientes debido a que dichas órbitas no están cerradas. A nivel cuántico, aparecen los niveles de energía de Landau; para campos magnético intenso estos niveles degeneran y todos los electrones libres acaban con energías en estos niveles de Landau, saltando entre ellos conforme dicho campo crece. Como resultado la conductividad eléctrica en el material se cuantiza, tomando valores a saltos, como los escalones de una escalera.
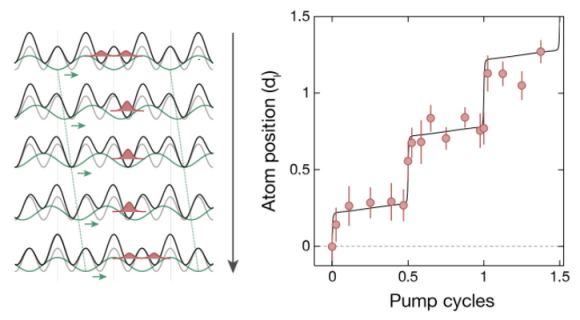
David J. Thouless, Nobel de Física de 2016, introdujo en 1983 el bombeo cuántico de carga, también llamado bombeo topológico, en un nanohilo (material 1D); al variar de forma periódica el potencial en el nanohilo la conductividad toma valores discretos en forma de escalera, apareciendo un análogo físico al efecto Hall cuántico entero en un material 2D. La implementación física más sencilla de este sistema se logra atrapando átomos ultrafríos en una red óptica 1D (obtenida con la superposición de dos ondas ópticas estacionarias); estos átomos saltan de un pozo de potencial a otro de forma controlada (mediante el cambio adecuado de la frecuencia de las ondas estacionarias). El espacio de fases 2D de un sistema Thouless 1D es un cilindro (o un toroide) y está caracterizado por un invariante topológico llamado primer número de Chern (de aquí que el bombeo se llame topológico).
Dos sistemas de Thouless acoplados entre sí tienen un espacio de fases 4D en forma de producto tensorial de dos cilindros (o dos toroides). Como cada sistema es un análogo físico al efecto Hall cuántico entero en un material 2D, los dos sistemas ortogonales se comportan como un análogo físico del efecto Hall cuántico entero en un material 4D. Para implementarlo basta usar un conjunto de átomos ultrafríos atrapados en una red óptica 2D (obtenida mediante tres ondas ópticas estacionarias de frecuencia adecuada); mediante la modulación periódica de los pozos de potencial de la red se logra el bombeo cuántico de carga que simula la conductividad en forma de escalera predicha por el efecto Hall en 4D.
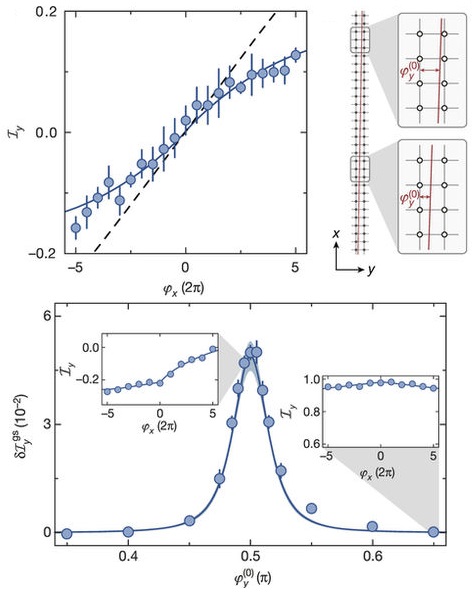
La dificultad del experimento se encuentra en verificar que los dos sistemas de Thouless son realmente ortogonales. Se sabe que en dicho caso el sistema estará caracterizado por un invariante topológico llamado segundo número de Chern y que aparecerá cierta respuesta no lineal en forma de sigmoide; dicha curva se considera señal inequívoca de dicho invariante topológico. Lohse et al. en Nature usan átomos de rubidio atrapados en un red óptica tridimensional obtenida superponiendo ondas estacionarias a λx = 767 nm, λy = 2 λx, y λz = 844 nm. Los resultados obtenidos se ajustan muy bien con las predicciones teóricas esperadas.
Por otro lado, un análogo óptico al efecto Hall cuántico entero en un material 2D se puede obtener con una serie (array) de guías ópticas paralelas entre sí, como ilustra la figura derecha. En general, estos cristales fotónicos son análogos ópticos a los sólidos cristalinos y presentan una estructura de bandas; lo más interesante es la aparición de bandas prohibidas para los modos propagantes que separan las bandas análogas a las de valencia y conducción en un sólido en las que sí se propagan; en las bandas prohibidas solo se pueden propagar modos evanescentes (similares a los modos superficiales en un material transparente). Se puede simular el bombeo de carga inyectando modos ópticos que saltan entre bandas prohibidas; inyectando luz en la primera guía se obtiene luz en la última guía, como ilustra la figura derecha. Este análogo físico al bombeo topológico resulta en un análogo físico al efecto Hall cuántico entero en 2D.
El bombeo topológico en 2D se puede simular mediante una matriz de guías ópticas (como la ilustrada en la figura que abre esta entrada), que ofrecerá un análogo físico al efecto Hall cuántico entero en 4D. Zilberberg et al. en Nature usan un sistema de 7 × 13 guías ópticas acopladas entre sí por modos evanescentes. Al inyectar luz con la frecuencia adecuada por la guía de la esquina inferior izquierda, como muestra esta figura, se observa una señal en las guías de la esquina superior derecha. Este fenómeno es la prueba experimental del bombeo topológico en 2D (en mi opinión esta prueba es menos firme que la obtenida en el otro artículo). Los resultados obtenidos están en buen acuerdo con las predicciones teóricos, lo que según los autores asegura que se ha logrado demostrar un análogo al efecto Hall cuántico entero en 4D.
En resumen, no hemos observado el reflejo 3D de un sistema físico 4D, ni se han revolucionado los fundamentos básicos de la ciencia actual. Se han publicado dos artículos que muestran sendos análogos físicos 2D al efecto Hall cuántico entero en 4D. Sin aplicación práctica tecnológica conocida, por ahora, estos análogos físicos permiten estudiar la física de sistemas topológicos de gran dimensión, luego son muy interesantes en investigación básica. Más aún, todo indica que pronto se obtendrán análogos del efecto Hall cuántico en 6D, e incluso en dimensiones más altas. Sin lugar a dudas uno de los campos más activos de la física es el estudio de propiedades topológicas en materiales 2D, el campo premiado con el Nobel de Física en 2016.