La fotónica topológica estudia los metamateriales planos (2D) cuyas propiedades ópticas emulan a los materiales topológicos en física de la materia condensada. El uso de fotones facilita la observación de ciertas transiciones de fase difíciles de observar con electrones. Como la transición de un punto de Dirac degenerado en cuatro puntos de Weyl conectados a pares por arcos de Fermi. Se han publicado en Science dos artículos que observan esta transición en cristales fotónicos artificiales. Estos metamateriales que incluyen incrustaciones metálicas permiten estudiar con detalle este proceso (inducido por pérdidas por radiación) y prometen futuras aplicaciones ópticas basadas en el pseudoespín que aprovechen la robustez topológica de estos estados.
Los artículos son Hengyun Zhou, Chao Peng, …, Bo Zhen, «Observation of bulk Fermi arc and polarization half charge from paired exceptional points,» Science 359: 1009-1012 (02 Mar 2018), doi: 10.1126/science.aap9859, y Biao Yang, Qinghua Guo, …, Shuang Zhang, «Ideal Weyl points and helicoid surface states in artificial photonic crystal structures,» Science 359: 1013-1016 (02 Mar 2018), doi: 10.1126/science.aaq1221; más información en Şahin K. Özdemir, «Fermi arcs connect topological degeneracies,» Science 359: 995-996 (02 Mar 2018), doi: 10.1126/science.aar8210. También recomiendo Wenlong Gao, Biao Yang, …, Shuang Zhang, «Experimental observation of photonic nodal line degeneracies in metacrystals,» Nature Communications 9: 950 (05 Mar 2018), doi: 10.1038/s41467-018-03407-5, y el artículo de revisión de Tomoki Ozawa, Hannah M. Price, …, Iacopo Carusotto, «Topological Photonics,» arXiv:1802.04173 [physics.optics].
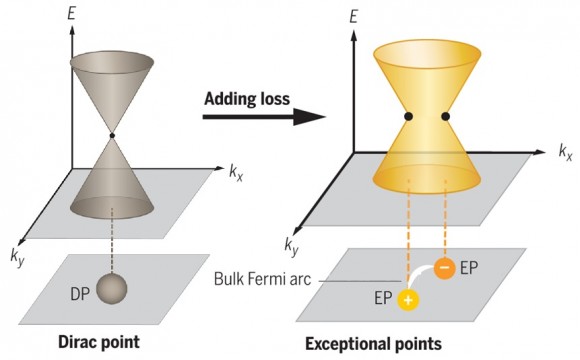
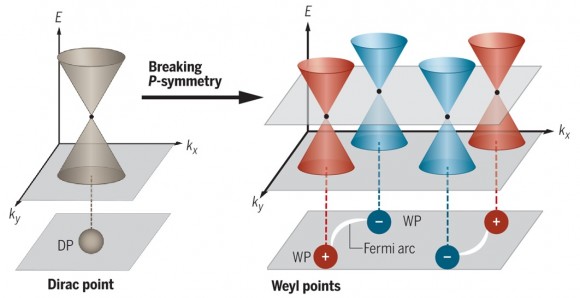
Los puntos de Dirac y de Weyl se comportan de forma muy diferente ante roturas de las simetrías de partidad (P) e inversión temporal (T). Para un punto de Dirac se rompe la degeneración y se abre un salto de banda (bandgap), con lo que el punto de Dirac pierde su robustez topológica. Sin embargo, para parejas de punto de Weyl de quiralidad opuesta la separación no es completa, ya que se mantienen conectados por un arco de Fermi, que preserva la robustez topológica. La rotura de la simetría T, respetando la simetría P, produce un pareja de puntos de Weyl conectados por arcos de Fermi; pero la rotura de la simetría P, respetando la simetría T, produce dos parejas de puntos de Weyl conectados por sendos arcos de Fermi.
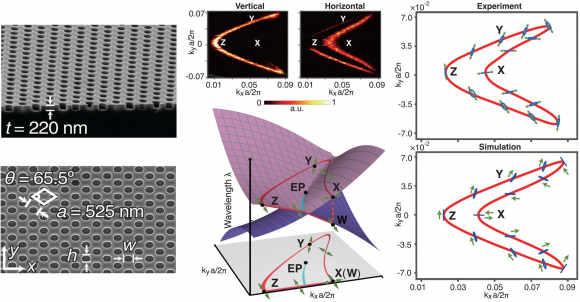
Yang et al. han usado un metamaterial fotónico para microondas. Los arcos de Fermi aparecen como superficies helicoidales en la estructura de bandas fotónicas que conectan los estados con carga topológica opuesta. Como el sistema no se comporta como un sistema físico hermítico (debido a las pérdidas por radiación), aparecen puntos excepcionales (EP) degenerados (en los que tanto los autovalores como los autovectores del operador están repetidos). Este comportamiento que no se observa en sistema hermíticos (que conservan la energía bajo la hipótesis de que no hay pérdidas) ofrecen un rico paisaje de estados topológicos por explorar.
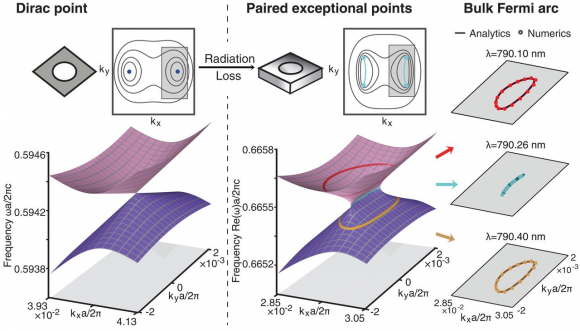
Zhou et al. observan arcos de Fermi en otro sistema no hermítico con cuatro puntos de Weyl resultado del cruce de modos longitudinales (LM) y transversales (TM). Estos puntos de Weyl están degenerados en energía (tienen la misma energía) luego tienen que estar conectados por arcos de Fermi. La gran ventaja de los cristales fotónicos respecto a los materiales topológicos es que es muy fácil explorar estos estados y observarlos con gran precisión.
Sin lugar a dudas los cristales fotónicos topológicos tendrán muchas aplicaciones, desde capas de invisibilidad, a superlentes con gran selectividad en frecuencia y angular, pero por ahora su relevancia se limita a ser análogos físicos. Su uso en ciencia básica nos permitirá aprender mucho sobre la conexión entre las propiedades topológicas y los sistemas que no son hermíticos (como los PT-invariantes). Un campo tan nuevo oculta muchos misterios. Conforme se vayan desvelando sus secretos más íntimos iremos concibiendo aplicaciones nicho para la fotónica topológica. Tiempo al tiempo, pero auguro que dentro de una década llegará un momento en el que nadie se acordará de que hubo un tiempo pasado en el que nadie estudiaba los materiales fotónicos no hermíticos.