El fondo cósmico de neutrinos (CνB) nos mostrará el universo cuando tenía un segundo; mientras que el fondo cósmico de microondas (CMB) nos lo muestra con unos 380 000 años. El CνB se puede observar de forma indirecta en las oscilaciones acústicas de bariones (BAO), que muestran un desplazamiento en fase inducido por estos neutrinos. Así se observó en 2015 en en el CMB y ahora se publica en Nature Physics su primera observación usando las observaciones de BOSS DR12 de las grandes estructuras del universo. Una nueva prueba que confirma la existencia del CνB que nos lleva a desear que los físicos jóvenes ideen nuevos métodos para su observación detallada durante este siglo.
Los neutrinos del CνB son casi imposibles de observar de forma directa, pues su energía actual se estima en 168 μeV (microelectrónvoltios); valor que hay que comparar con los cientos de keV (kiloelectrónvoltions) que tienen los neutrinos de menor energía que hemos podido observar. Ahora mismo la única opción posible es la observación indirecta. Cuando se formó el CMB los neutrinos daban cuenta del 10% de la densidad total del universo; gracias a ello los neutrinos del CνB influyen en las BAO que se pueden observar en el CMB. La nueva observación se basa en los datos finales (DR12) de BOSS (Baryon Oscillation Spectroscopic Survey) que ha estudiado 1 198 006 galaxias con desplazamientos al rojo espectroscópicos entre 0.2 < z < 0.75. El espectro de las BAO muestra la oscilación inducida por los neutrinos al 95% CL (unas dos sigmas). Las futuras observaciones de DESI (Dark Energy Spectroscopic Instrument) prometen alcanzar las tres sigmas.
La futura generación de telescopios espaciales para la observación del CMB permitirá lograr una observación (indirecta) del CνB hasta cinco sigmas. Sin lugar a dudas estamos viviendo una época apasionante en cosmología. El artículo es Daniel Baumann, Florian Beutler, …, Christophe Yèche, «First constraint on the neutrino-induced phase shift in the spectrum of baryon acoustic oscillations,» Nature Physics (25 Feb 2019), doi: 10.1038/s41567-019-0435-6, arXiv:1803.10741 [astro-ph.CO]; más información divulgativa en Ethan Siegel, «Earliest Signal Ever: Scientists Find Relic Neutrinos From 1 Second After The Big Bang,» Starts With A Bang, 28 Feb 2019.

Las oscilaciones acústicas de bariónes aparecieron cuando la materia y la radiación se desacoplaron. Antes de este momento la temperatura media del universo era de varios miles de grados, con los fotones interaccionando fuertemente con los electrones del plasma mediante dispersión de Compton; así la radiación (fotones) y la materia (bariones) se comportaban como un único fluido. Este fluido fotón-barión está sometido a dos fuerzas opuestas, la atracción gravitacional de la materia y la presión de radiación de los fotones. Como resultado, cualquier perturbación en la densidad de la materia bariónica provoca una oscilación que se propaga como una onda de presión amortiguada (de ahí el término «oscilacione acústicas» en analogía con el sonido).
Tras el desacoplamiento de la materia y la radiación, las oscilaciones de densidad quedan «congeladas», lo que deja una huella impresa en el CMB y en la distribución de galaxias a escala cósmica. En esta última se observa al estudiar la distribución de las distancias entre galaxias; como si las galaxias se distribuyeran en «cascarones» esféricos, que en la actualidad deben tener un radio de unos 150 Mpc (megapársec) y un grosor de unos 30 Mpc. La imagen artística de más arriba trata de ilustrar esta idea (APOD, 20 Jan 2014).
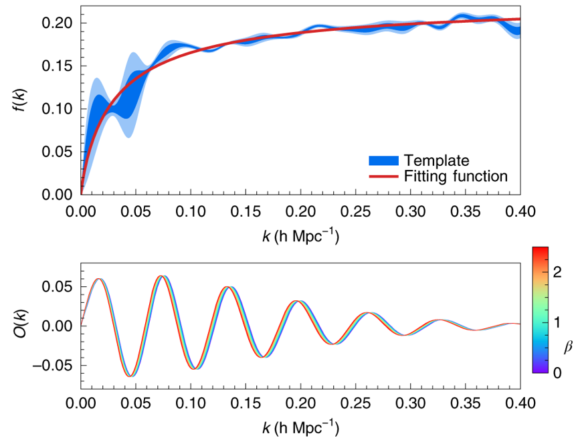
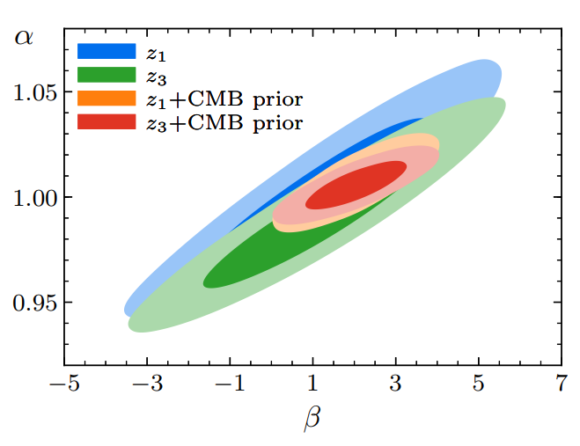
El efecto de los neutrinos del CνB sobre las BAO se observa en un pequeño cambio de fase en su espectro. El efecto se caracteriza con dos parámetros α (que caracteriza las BAO) y β (que caracteriza el desfase debido a los neutrinos); su valor de referencia según el modelo es la unidad. Para el primero tenemos medidas muy precisas, α = 1.000 ± 0.032 (0.2 < z < 0.5, llamado z1 en la figura que abre esta entrada) y α = 1.000 ± 0.035 (0.5 < z < 0.75, llamado z3 en dicha figura). Para el segundo las medidas son mucho más imprecisas, pues la contribución de los neutrinos es muy pequeña. Por eso ha habido que esperar al análisis de todos los datos de BOSS (DR12) para observar un valor de β = 0.8 ± 2.3, que va en contra de la hipótesis nula (que no contribuyan los neutrinos del CνB y resulte β = 0) con una significación σ(β) = 2.1 (unas dos sigmas).
Para los estándares de la física de partículas, dos sigmas puede parecer una significación paupérrima. Pero en cosmología (y otras áreas de la ciencia) se trata de un resultado relevante dadas las enormes dificultades de la observación (de ahí que se haya publicado en Nature Physics). Lo destacable es que esta medida, junto con la confirmación previa de 2015 basada en el CMB, muestran que el CνB existe. Así se abre la puerta para diseñar futuros métodos de observación más precisos que acaban conduciendo a un mapa del CνB (lo que sería la primera foto del universo cuando tenía solo un segundo). ¿Se podrá lograr durante este siglo? No lo sabemos, pero podemos soñar con ello.


Muy Interesante la entrada, sí señor.
Gracias 🙂
Excelente noticia. Gracias, Francis.
Y una duda no menor: ¿dispersión de Compton o de Thomson?
Es que acerca de «Baryon Acoustic Oscillation» y/o «Primordial Plasma» y/o «Baryon-Photon Fluid» he visto muchas fuentes que ponen «Compton scattering» y otras tantas (entre éstas la Wiki) que ponen «Thomson scattering».
El libro Cosmology for Physicists (2016) de David Lyth, en el apartado 13.2 Baryon Acoustic Oscillation, pone énfasis en ello:
«Since the typical photon energy is much less than the electron’s rest energy, its scattering off an electron leaves its energy almost unchanged (Thomson scattering as opposed to Compton scattering)…»
Desde ya muchas gracias. Saludos.
Pelau, como bien sabrás la dispersión de Thomson es el límite no relativista de la dispersión de Compton; para calcular el término principal de las BAO basta usar la dispersión de Thomson, pero la dispersión de Compton introduce correcciones relativistas que hay que tener en cuenta si quieres ir más allá en el desarrollo perturbativo. Así que tu elección depende de la precisión que necesites.
Para el análisis de este artículo en concreto solo se usa el término principal, así que Thomson es suficiente.
Intuía que por ahí venían los tiros, pero así da gusto.
Muchísimas gracias, Francis.
Entiendo que la afirmación de este artículo ya no es válida (el fondo cósmico de neutrinos es mas reciente que el fondo cosmico de microondas), ¿qué es lo que ha fallado?
https://francis.naukas.com/2009/10/20/el-fondo-cosmico-de-neutrinos-es-mas-reciente-que-el-fondo-cosmico-de-microondas/
Gracias, pspe2, por recordar dicho artículo. El fondo cósmico de microondas no surgió de repente a los 380 000 años, sino que tiene una anchura espectral, es decir, contiene fotones que han ido apareciendo entre los 100 000 y los 380 000 años (aunque por ahora no sabemos distinguirlos, en un futuro se pretende lograrlo).
Lo mismo ocurre con el fondo cósmico de neutrinos, que no surgió de repente cuando el universo tenía un segundo y una temperatura de 1 MeV; si los neutrinos no tuvieran masa, su anchura sería pequeña y todos serían anteriores a los fotones del CMB; sin embargo, el artículo de Scott Dodelson y Mika Vesterinen observaba que si los neutrinos tenían una masa grande, podría ocurrir que la anchura espectral fuera tan ancha que el fondo cósmico de neutrinos incluyera neutrinos más recientes que los fotones del CMB.
En sus cálculos de 2009 consideraban que el neutrino con mayor masa tuviera entre 0.05 y 1 eV; hoy sabemos que tiene una masa menor de 0.15 eV, pero aún no sabemos si es mayor de 0.05 eV. En este último caso, el CNB podrían contener neutrinos observables como más «recientes» que los fotones del CMB. Esto no afecta a los resultados de BOSS BAO DR12; el desacoplamiento de los neutrinos empezó a ocurrir cuando el universo tenía un segundo, sin que influya desde cuándo los podemos observar a día de hoy.
Un artículo reciente (te recomiendo la figura 1) sobre este asunto es Yin-Zhe Ma, Douglas Scott, «How much cosmological information can be measured?» Phys. Rev. D 93: 083510 (2016), doi: 10.1103/PhysRevD.93.083510, arXiv:1510.08309 [astro-ph.CO].