En la gravitación de Einstein la «carga» gravitacional es la densidad de energía y momento lineal, en lugar de la masa como en la teoría de Newton. Luego toda partícula con energía cinética positiva se mueve a lo largo de una geodésica. Sabemos desde el descubrimiento de la antimateria en 1932 que las antipartículas tienen energía cinética positiva, como las partículas. Por tanto, no hay ninguna diferencia en la caída libre de un átomo y un antiátomo. En ciencia todo debe ser comprobado con un experimento, en este caso la universalidad de la caída libre. Se publica en Nature que el experimento ALPHA-g del CERN ha estudiado la caída libre de átomos de antihidrógeno (formados por un antiprotón y un positrón). Almacenaron átomos de antihidrógeno en una trampa de Penning con campos magnéticos; con dicha trampa en vertical, los liberan bajo la aceleración terrestre, para contar el número de antiátomos que caen hacia abajo y los que «caen hacia arriba». Lo complicado es reducir los campos magnéticos de la trampa a cero. Los experimentos muestran que los átomos de antihidrógeno caen igual que los átomos de hidrógeno, sin ninguna diferencia. Un experimento sencillo pero que requiere una gran pericia técnica.

Quizás hayas leído que este tipo de experimentos son necesarios para comprobar el principio de equivalencia newtoniano entre la «masa inercial» y la «masa gravitatoria». La diferencia entre estos conceptos newtonianos no tiene ningún sentido en un física relativista. A pesar de ello, muchos físicos y astrofísicos han especulado en artículos científicos con la idea de que el cociente entre la masa inercial (m) y la masa gravitatoria (m_g) sea m/m_g = −1 para la antimateria y m/m_g = +1 para la materia; en dicho caso, en la caída libre de un antiátomo se observaría un movimiento en el sentido opuesto a la de un átomo. Pero recuerda que si así fuera ya lo sabríamos desde hace décadas, pues se habría observado la diferencia en los rayos cósmicos (que se usaron para descubrir el positrón en 1932). Nunca se ha observado ninguna diferencia, pero dicha observación se considera indirecta. El experimento ALPHA-g ha realizado la observación directa de que el antihidrógeno se comporta como el hidrógeno en una caída libre, como predice el principio de equivalencia einsteiniano. Dudar de todo es parte intrínseca de la ciencia. Por ello este tipo de experimentos deben ser realizados.

En algunos medios se afirma que este tipo de experimentos son el primer paso para entender la gravitación cuántica más allá del modelo estándar. Que no te confundan, no es cierto. Este tipo de experimentos no puede aportar ninguna información relevante para el descubrimiento de la futura teoría cuántica de la gravitación. El artículo es E. K. Anderson, C. J. Baker, …, J. S. Wurtele, «Observation of the effect of gravity on the motion of antimatter,» Nature 621: 716-722 (27 Sep 2023), doi: https://doi.org/10.1038/s41586-023-06527-1; información divulgativa en Anna Soter, «Free-falling antihydrogen reveals the effect of gravity on antimatter,» Nature 621: 699-700 (27 Sep 2023), doi: https://doi.org/10.1038/d41586-023-02930-w.

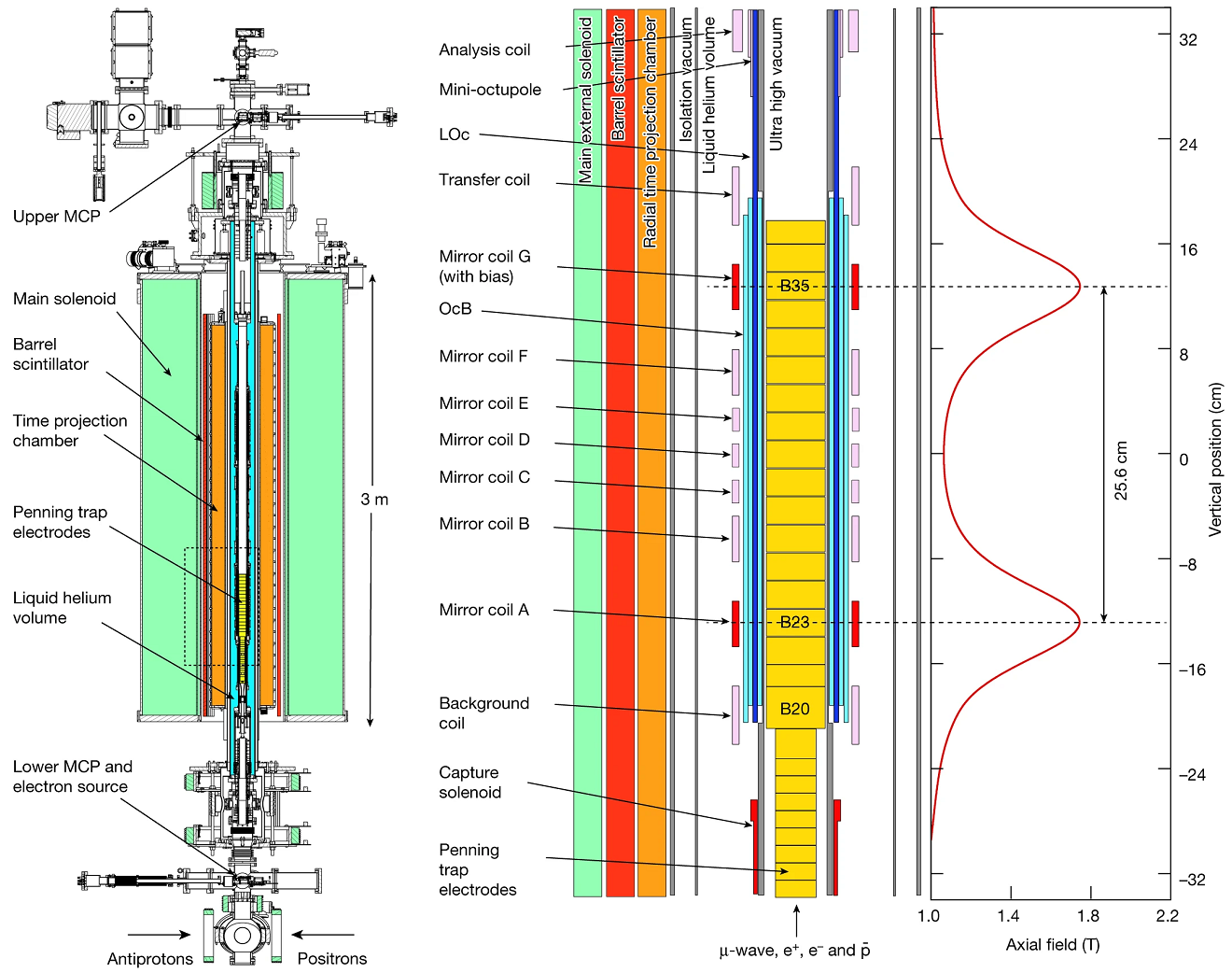
Lo complicado de un experimento para medir la caída libre de un antiprotón es garantizar que la única aceleración aplicada es la gravedad en la superficie de la Tierra. Para un antiprotón enfriado a una temperatura de 10 K dicha aceleración equivale a un campo eléctrico de unos 10⁻⁷ V/m, o a un campo magnético de unos 10⁻¹⁰ T. La única forma de hacer el experimento es usar antimateria neutra, como átomos de antihidrógeno. La colaboración ALPHA montó en 2018 una trampa magnética de Penning orientada en vertical, el experimento llamado ALPHA-g, para estudiar la caída libre. La idea es sencilla: atrapar y acumular miles de átomos de antihidrógeno; liberarlos de forma lenta los que están en la parte superior e inferior de la trampa (abriendo las barreras de potencial); discernir cómo influye la aceleración de la gravedad en su movimiento cuando escapan y se aniquilan en las paredes materiales del aparato. La idea es sencilla, se observará en una diferencia en el número de aniquilaciones de los antiátomos que escapan por la parte superior y por la parte inferior de la trampa. Pero la realización práctica es muy complicada. Por ejemplo, los antiátomos atrapados no están en reposo; su energía cinética presenta una distribución estadística equivalentes a una temperatura de unos 0.5 K.

El diseño experimental se muestra en la figura. La carga de antiátomos se inicia con la carga de antiprotones generados del CERN Antiproton Decelerator y el anillo ELENA (Extra Low ENergy Antiproton) que se inyectan en una trampa de Penning con un solenoide de 3 T (teslas). Desde ELENA se inyectan unos 7.5 millones de antiprotones con una energía cinética de 100 keV cada 120 segundos. Se capturan unos 500 mil que se enfrían antes de inyectarlos en ALPHA-g, donde un solenoide superconductor los confina en un campo magnético de 1 T. Allí se inyectan unos 3 millones de positrones. El resultado es la formación de átomos de antihidrógeno de baja energía cinética atrapados en un campo magnético; los antiátomos están polarizados en espín y se enfrían a unos 4 K usando helio líquido. En cada ciclo de carga ALPHA-g atrapa unos pocos átomos de antihidrógeno; que se pueden acumular tras muchos ciclos de carga desde ELENA. Este proceso se llama «apilamiento» de antihidrógenos; el volumen de captura es un cilindro vertical de 4.4 cm de diámetro y 25.6 cm de altura.

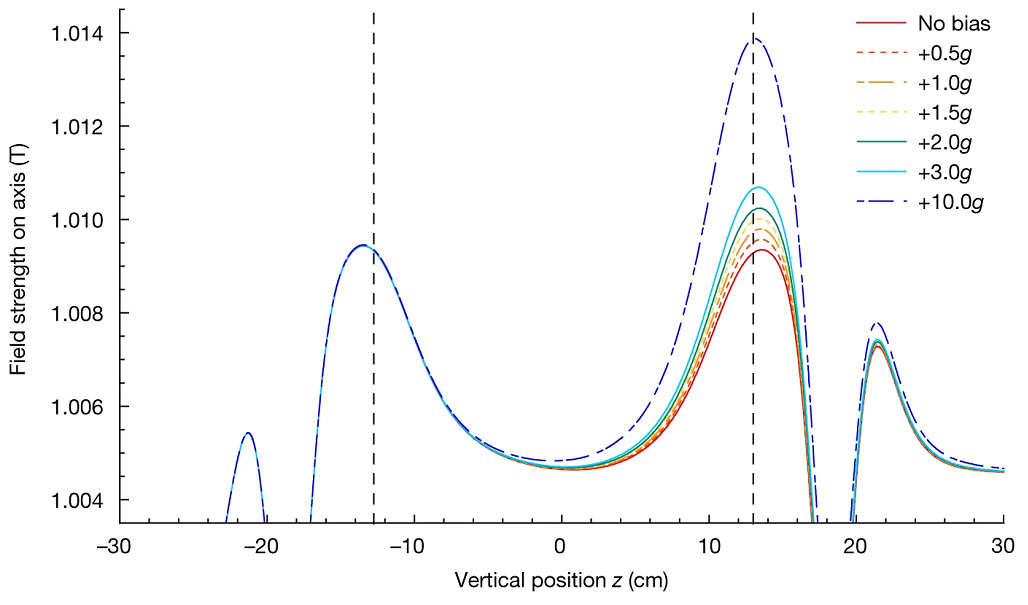
Para observar los efectos de la aceleración de la gravedad se usan parejas de bobinas magnéticas llamadas bobinas espejo (mirror coills). Se liberan los antihidrógenos de la trampa reduciendo la corriente aplicada en las dos bobinas de espejo más extremas (llamadas A y G en el experimento) de forma simultánea durante 20 segundos. Los antiátomos escaparán hacia la parte superior de la trampa a través de la bobina espejo G o hacia la parte inferior a través de la bobina espejo A; en ambos casos acabarán aniquilados en las paredes del aparato. Se detectarán las posiciones y el instante de las aniquilaciones mediante detectores de centelleo para determinar el llamado tiempo radial proyectado (rTPC). Sin aplicar la corriente eléctrica (no bias), la aceleración de la gravedad terrestre (g = 9.81 m/s²) equivale a 4.53 × 10⁻⁴ T entre los dos máximos de la trampa separados 25.6 cm. En la figura se ilustra la aplicación de la corriente en la bobina espejo G, sin aplicarla en la A, lo que conduce a una aceleración positiva que crece desde +0.0 g hasta unos +10.0 g (como se ilustra en la figura); si se aplica a la bobina A y no a la G la aceleración será negativa. Según las simulaciones numéricas la liberación lenta de los antihidrógenos durante 20 segundos conducirá a que el 80 % de ellos saldrá por el fondo y el 20 % restante por arriba.

El experimento ha de ser repetido muchas veces (la toma de datos duró 30 días), resultando una serie de histogramas con la cuenta de los antihidrógenos que se liberan por arriba (Up) y por abajo (Down). Esta figura muestra los resultados finales (en formato original, sin correcciones de fondo o asociadas a la eficiencia de los detectores). Se observan que recorren desde −10 g hasta +10 g (solo se han contado los antihidrógenos que se emiten entre el segundo 10 y el 20, pues por debajo del segundo 10 su número es insignificante). Los resultados finales (la llamada curva de escape) es la que se muestra al principio de esta pieza (te recomiendo volver a verla). Se observa que los datos experimentales siguen la curva predicha en el caso de que la aceleración de la gravedad terrestre influya en el número de antihidrógenos que escapan hacia arriba y hacia abajo; los datos ni siguen la curva predicha sin aceleración de la gravedad, ni mucho menos la curva predicha si su «masa gravitatoria» fuera negativa.

La concordancia entre los datos y la simulación es convincente, con un acuerdo cualitativo excelente. Sin embargo, a nivel cuantitativo hay diferencias, pues los antihidrógenos se comportan como si la aceleración de la gravedad que actúa sobre ellos fuera algo menor de g, en concreto de (0.75 ± 0.13 (estadístico + sistemático) ± 0.16 (simulación)) g, con g = 9.81 m/s². Este resultado equivale a (0.75 ± 0.20) g, valor que está a 1.3 desviaciones estándares del valor esperado 1 g. En el artículo se afirma que una análisis de la verosimilitud del resultado permite estimar una probabilidad de 2.9 × 10⁻⁴ de que el resultado se ha debido a una fluctuación aleatoria bajo la hipótesis de que la aceleración de la gravedad no actúa sobre el antihidrógeno en este experimento. Por ello, los autores afirman que se descarta la existencia de una aceleración de la gravedad negativa sobre la antimateria. Obviamente, en la primera realización de un experimento tan complicado no se puede esperar un mejor acuerdo con la teoría. Futuros experimentos más refinados tendrán que reducir estos errores para lograr un mejor acuerdo con la predicción teórica. Porque nadie espera ninguna desviación con la predicción teórica de la gravitación einsteniana. Además, deberán ser confirmados por otros experimentos como GBAR42 y AEgIS43 en el CERN. Pero, repito lo que ya dije al principio, nadie espera que la relatividad general de Einstein esté equivocada cuando se aplica a la antimateria.