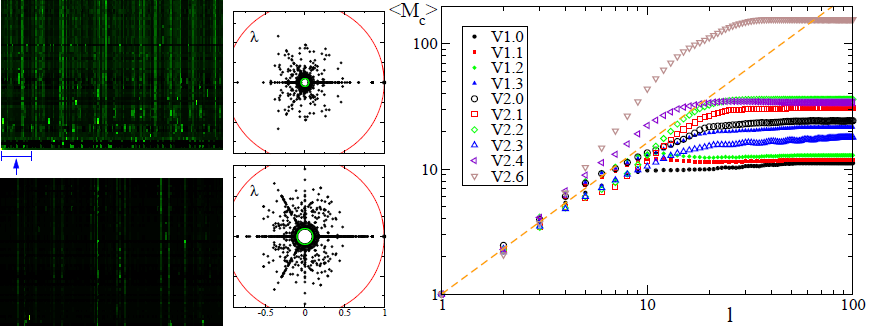
Los que hemos publicado más de un artículo científico/técnico con la palabra «fractal» en el título sabemos que encontrar fractales por doquier es fácil. El núcleo (kernel) del sistema operativo Linux está formado por una complicada red de programas (subrutinas) que se llaman mutuamente entre ellos. La aplicación del algoritmo PageRank que utiliza el buscador Google permite estudiar las propiedades de esta red de llamadas. El espectro de autovalores y autovectores de la matriz de Google resultante presenta una geometría fractal caracterizada por una dimensión (fractal) no entera. El análisis de 14079, 85756 y 285509 llamadas a subrutina en el kernel de las versiones 2.0.40, 2.4.37.6 y 2.6.32, respectivamente, de Linux muestra que la dicha dimensión fractal es constante e igual aproximadamente a 1’2. ¿Con qué comparar este número? Un análisis similar para la estructura fractal de la WWW (internet) muestra que tiene una dimensión fractal de 4’1. Más aún, para redes con dimensión fractal menor de 2 se puede aplicar la ley de Weyl que caracteriza la red mediante un exponente (fractal). El exponente de Weyl para el kernel de Linux es 0’63 (para la WWW dicha ley no es aplicable). Un análisis interesante sobre todo para los interesados en teoría de redes y un resultado curioso para todos los aficionados a Linux. Saberlo, servir, lo que se dice servir, no sirve para nada, pero seguro que muchos frikis presumen de recordar estos números en más de una campus party. El artículo técnico sobre Linux es L. Ermann, A. D. Chepelianskii, D. L. Shepelyansky, «Fractal Weyl law for Linux Kernel Architecture,» ArXiv, 9 May 2010, y el artículo técnico sobre la WWW (ya aceptado en Phys. Rev. E) es B. Georgeot, O. Giraud, D.L. Shepelyansky, «Spectral properties of the Google matrix of the World Wide Web and other directed networks,» ArXiv, 17 Feb 2010.
¿Matriz de Google? Un grafo dirigido, conjunto de nodos unidos por flechas, se caracteriza bien gracias a una matriz de Google
que se construye a partir de los arcos dirigidos entre los nodos de la forma
, donde la matriz
se obtiene normalizando a la unidad todas las columnas de la matriz de adyacencia (matriz con un uno en la posición
si hay un arco entre dichos nodos y un cero en caso contrario), reemplazando las columnas cuyos elementos son cero por
, donde
es el número total de nodos. El parámetro de relacjión
describe la probabilidad de alcanzar un nodo de la red tomando un arco aleatorio. Para
el único autovector con
es llamado vector de PageRank.