El verano es la época ideal para conversar. En los últimos días Amarashiki (TSOR), Alejandro Rivero (@arivero,web) y Kac-Moody (@1KacMoody1) han mantenido una interesante charla sobre la supergravedad (Sugra) y las teorías de Kaluza-Klein (KK) en Twitter sobre la cuestión «¿por qué se abandonó la línea de investigación en [teorías de Kaluza-Klein y Sugra] en 1985?,» que surgió al hilo de la entrada de Alejandro como invitado en mi blog («Lo que pudo haber sido«). No soy experto en estas lides, pero yo creía que la razón estaba bastante clara: la primera revolución de la teoría de supercuerdas en el verano de 1984 y los problemas que antes de dicho verano se habían detectado en las teorías de supergravedad en 11 dimensiones relacionados con la quiralidad del modelo estándar y con sus divergencias ultravioletas (se trata de una teoría no renormalizable). Para los expertos en Kaluza-Klein y supergravedad cambiar de tópico de trabajo a la teoría de supercuerdas prometía muchos más éxitos. Por todo ello creo que fueron abandonadas estas ideas. Como sus problemas aún no han sido resueltos y se cree que no tienen una solución elegante, siguen abandonadas. Permíteme recordar la situación de las teorías de Kaluza-Klein y de supergravedad antes del verano de 1984 (me basaré, como no, en M.J. Duff, B.E.W. Nilsson, C.N. Pope, «Kaluza-Klein Supergravity,» Physics Reports 130: 1-142, 1986, y en M.J. Duff, «Supergravity, Kaluza-Klein and superstrings,» pp. 18-60 en 11th Intl. Conf. General Relativity and Gravitation, Cambridge UP, 1987).
Los físicos creemos que la realidad está formada por dos entidades básicas: espaciotiempo curvado (la gravedad) y campos cuánticos (el modelo estándar). Hay dos caminos posibles para una «teoría de todo» que unifique ambas entidades en la escala de Planck. El primero es que todo es espaciotiempo curvado y por tanto los campos (cuánticos) son el resultado de la existencia de dimensiones extra del espaciotiempo muy curvadas y de forma muy compacta. Copar con campos clásicos es fácil y esta es la idea de las teorías de Kaluza-Klein y de la supergravedad; sin embago, en el caso cuántico hay un grave problema, esta teoría no es renormalizable, como tampoco lo es la versión cuántica de la gravedad de Einstein, y por tanto no puede ser válida en la escala de Planck.
Y el segundo camino es que todo son campos cuánticos y el espaciotiempo es una entidad emergente, aunque por el momento no tenemos muy claro cómo emerge. Hay muchas propuestas en diferentes grados de desarrollo. La más popular y la que presenta un mayor grado de evolución es la asociada a campos cuánticos «cuerdísticos» (la generalización de los campos de partículas «puntuales» a campos de cuerdas y branas), en la llamada teoría de cuerdas y teoría M (ST/MT). Gracias a la simetría del espejo («mirror symmetry») y a la dualidad T se sabe que en esta teoría no existen las distancias menores que la longitud de Planck, aunque la descripción detallada de la teoría a esta escala no es conocida en detalle. Sin embargo, hay muchas otras ideas para entender la emergencia del espaciotiempo; sin ser exhaustivo me vienen a la cabeza las siguientes posibilidades (todas en un grado de desarrollo que podemos calificar como «pobre» comparado con ST/MT y cuya consistencia interna está sujera a grandes dificultades técnicas aún no resueltas): las ideas asociadas a la gravedad cuántica de bucles (LQG), las ideas asociadas al principio holográfico, las asociadas a la causalidad de las interacciones entre campos como la teoría de triangulaciones dinámicas causales (CDT), y las asociadas a fuerzas entrópicas entre los campos como en la teoría de la gravedad entrópica de Erik Verlinde. Para evitar malentendidos, me gustaría recalcar que la única teoría de gravedad cuántica consistente hasta el momento es la ST/MT y que en la actualidad hay físicos tratando de incorporar las demás ideas en el marco ST/MT con objeto de transformarlas en teorías consistentes.
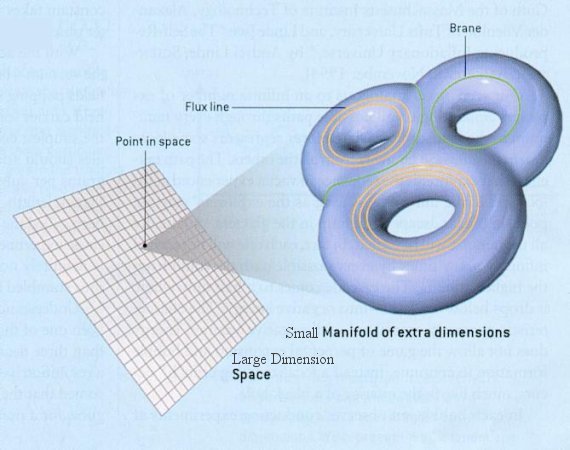
Volvamos a la idea de Kaluza-Klein, impecable a nivel clásico. Las ecuaciones de la gravedad de Einstein para un espaciotiempo con D>4 dimensiones describen además del gravitón (partícula de espín 2), bosones gauge (partículas de espín 1 descritas por ecuaciones de Yang-Mills) y bosones escalares llamados dilatones (de espín cero que se puede hacer que actúen como bosones de Higgs). La topología de las D – 4 dimensiones extra es diferente del resto, son compactas (cerradas y acotadas, como una esfera o un toroide), por lo que tienen un tamaño finito. Las simetrías del modelo estándar, SU(3)xSU(2)xU(1), se pueden incorporar tomando un grupo G de simetría que contenga a SU(3)xSU(2)xU(1) y compactificando las dimensiones extra con una variedad diferenciable cuyo grupo de isometría sea G (a este idea se le suele llamar graviGUT, porque el grupo G define una teoría de gran unificación o GUT).
¿Por qué no observamos las D – 4 dimensiones extra del espaciotiempo? En las teorías de Kaluza-Klein las cargas (gauge) son proporcionales a la constante de Newton de la gravedad y el factor es una función inversa al tamaño de las dimensiones extra; como las cargas gauge son muy grandes comparadas con la gravedad, recuerda que es muy débil, las dimensiones extra tienen un tamaño muy pequeño. Lo habitual es tomar la escala de Planck (unos 10-33 cm). La versión cuántica de la teoría implica la existencia de nuevas partículas asociadas a campos confinados en las dimensiones extra campactas, llamadas partículas de Kaluza-Klein; no observamos estas partículas porque su masa es del orden de la energía de Planck (unos 1019 GeV).
Las teorías de Kaluza-Klein (o teorías graviGUT) tienen muchos problemas, pero mencionaré sólo tres de ellos. El primero es que la teoría no incorpora fermiones (leptones y quarks), que como en el caso del modelo estándar, han de ser introducidos ad hoc como en cualquier otra teoría GUT (luego no se trata de una teoría de todo, sino de «casi todo»). El segundo es que la versión cuántica de estas teorías no es renormalizable (los problemas que aparecen al cuantizar la gravedad de Einstein en 4 dimensiones se mantienen en D dimensiones). Y el tercero que mencionaré es que la teoría no es quiral, a diferencia del modelo estándar, y no se conoce ningún mecanismo de rotura espontánea de la simetría que rompa una teoría no quiral en una teoría quiral. Que no me peguen los expertos. Se han publicado soluciones a estas problemas, pero no son del todo satisfactorias. Por ejemplo, en lugar de usar las ecuaciones de Einstein para la gravedad que tienen derivadas hasta el segundo orden, como las ecuaciones de Newton, se puede usar una generalización con infinitas derivadas cuya versión cuántica parece ser renormalizable, pero que mantiene otros problemas.
Una solución natural para incorporar fermiones en una teoría de Kaluza-Klein es utilizar la supersimetría, que conduce a la teoría llamada supergravedad. La supersimetría es una simetría que transforma fermiones en bosones y viceversa. Además, aplicar dos transformaciones supersimétricas equivale a una traslación en el espaciotiempo, es decir, la supersimetría equivale a una raíz cuadrada de una traslación (SUSY2=TRASLACIÓN). La supergravedad es la teoría tipo gauge basada en la supersimetría como simetría local y no hay que meter de forma explícita las ecuaciones de Einstein, ya que esta teoría incluye una partícula de espín 2, que actúa como gravitón, y la gravedad aparece de manera natural (algo parecido ocurre en QED al hacer la simetría U(1) local aparece el electromagnetismo como arte de magia). Asociado al gravitón hay partículas de espín 3/2 llamados gravitinos; su número es igual al número de supersimetrías diferentes de la teoría. Hay varias razones teóricas en contra de la existencia de partículas de espín mayor de 2, por lo que el número máximo de supersimetrías es N=8. Este número de supersimetrías determina el espectro completo de partículas. Por ejemplo, para N=8 supersimetrías hay un supermultiplete que contiene un gravitón (espín 2), 8 gravitinos (espín 3/2), 28 bosones vectoriales (espín 1), 56 fermiones de espín 1/2, y 70 bosones escalares (espín 0).
Una teoría de todo debe ser única (en algún sentido) y la supergravedad es única en D=11 dimensiones. La razón es que el número de supersimetrías impone un número máximo de dimensiones para el espaciotiempo. Como el número de supersimetrías es N≤8 y un espinor de Dirac en 4 dimensiones tiene 4 componentes, el número máximo de componentes permitido para un espinor de Dirac en D dimensiones debe ser 32 lo que obliga a que D≤11 (el número de componentes de un espinor de Dirac es igual a 2(D-1)/2 para D impar y 2D/2 para D par). El espaciotiempo tiene 4 dimensiones, luego la teoría en 11 dimensiones debe tener 7 dimensiones extra compactificadas en el sentido de las teorías de Kaluza-Klein.
La dualidad entre supergravedades (N=1 en D=11)↔(N=8 en D=4) es muy sugerente y llevó a prestar mucha atención a la (única) teoría de la supergravedad N=1 en D=11 dimensiones. La gravedad en esta teoría descrita por un tensor métrico de 44 grados de libertad (componentes del campo del gravitón) y un gravitino de 128 componentes. La supersimetría obliga a que aparezcan campos bosónicos de 84 componentes (84+44=128). Además de aparecer las ecuaciones de Einstein sin ser impuestas, también surge la separación de las dimensiones extra M11=M4xM7, cuando el tensor de cuatro índices de intensidad del campo gauge de 84 componentes es constante (es decir, lo más simple posible). La fenomenología de la teoría N=8 en D=4 da muchos problemas y es preferible una teoría N=1 en D=4; a principios de los 1980 hubo mucho revuelo cuando se descubrió que tomando M7=S7 (la esfera en 7 dimensiones) aparece de forma natural un mecanismo de Higgs que rompe la supersimetría N=8 en D=4 en la supersimetría N=1 en D=4, pero su grupo de holonomía H(M7)=G2 que implica un grupo gauge SO(8) que no es suficiente para contener el modelo estándar SU(3)xSU(2)xU(1). Hay otras propuestas para M7 que permiten grupos más grandes capaces de albergar el modelo estándar, pero ninguna admite una rotura de simetría «natural» hasta N=1.
Volvamos al principio, ¿por qué se abandonó la idea de la supergravedad N=1 en D=11 tras el verano de 1984 cuando en 1983 podríamos decir que había euforia por ella? Como es obvio influyó la primera revolución de la teoría de cuerdas, la teoría de supercuerdas de 1984, pero hay razones más importantes que están descritas en todos los artículos de revisión sobre esta teoría. Destacaré tres de ellas.
La primera es un artículo de Edward Witten que mostró que una supergravedad en D=11 con dimensiones extra compactificadas en una variedad diferenciable no puede ser rota de forma espontánea a una teoría quiral en D=4 dimensiones. Si la teoría no es quiral en D=11 entonces tampoco lo puede ser en D=4 (la quiralidad se preserva en dimensiones impares y sólo puede surgir en la rotura de simetría en espaciotiempos con dimensión par). Para resolver este problema se puede «complicar» la teoría en D=11 introduciendo ad hoc la quiralidad o usando simetrías «ocultas», pero la unicidad, la simplicidad y la belleza de la teoría desaparece. Los pocos expertos que siguieron investigando en supergravedad tras la revolución de la teoría de cuerdas se concentraron en la teoría en D=10 dimensiones. Pero los fermiones quirales tienen asociados la aparición de anomalías quirales que violan las simetrías gauge de la teoría Yang-Mills en D=4; se pensó que podrían ser eliminadas con una compactificación adecuada, pero se demostró en 1983 que dicha compactificación no existe. Para resolver este problema basta compactificar en una variedad que no sea diferenciable (como una red discreta), pero a mucha gente no le gusta esta idea porque no se puede recuperar de forma fácil el modelo estándar.
La segunda razón por la que en 1985 se relegó a un segundo plano la idea de la supergravedad N=1 en D=11 fue que la compactificación de las dimensiones extra introduce una constante cosmológica enorme, proporcional a la masa de Planck al cuadrado; en aquel momento se pensaba que la constante cosmológica era nula (hoy sabemos que existe la energía oscura, pero la constante cosmológica es unos 120 órdenes de magnitud más pequeña que la masa de Planck al cuadrado). Hoy en día se pueden reducir estos 120 órdenes de magnitud a menos de 60 (según los detalles técnicos), un número que sigue siendo enorme.
La tercera razón, quizás la más importante es que la teoría no es renormalizable y presenta divergencias ultravioletas. Ha habido progresos recientes en la renormalización de «la supergravedad N=8» (yo los califiqué en este blog de forma muy optimista como «una nueva revolución en la física teórica«), pero el problema de fondo sigue siendo el mismo. Aunque la teoría sea renormalizable hasta 5 bucles, hay argumentos fuertes en contra a partir de 7 bucles, inclusive. Hoy en día no parece que la teoría pueda ser renormalizable a todos los órdenes. La teoría de cuerdas, por el contrario, parece finita a todos los órdenes.
En resumen, espero que esta entrada aclare un poco mi opinión sobre este asunto que se discutió en Twitter y espero que en los comentarios, si os apetece, continuemos el debate, si os sigue suscitando interés.
PS: Todos los comentarios de esta entrada han sido eliminados. 18 agosto 2013 14:00 pm


Francis, te agradezco mucho que hayas hecho el esfuerzo de explicar las cosas para todos de una forma ordenada porque ayer intentaba leer y seguir los tuits pero me resultaba imposible y lo dejé estar. Así puedo irlo siguiendo de una forma más organizada y si vais aportando ideas podré asimilarlas.
Me interesa conocer las teorías que se cuecen aunque la lástima es que sin el aparato matemático no se puede entender porqué han llegado a eso o porque son necesarias ese número concreto de dimensiones. Bueno, estaré pendiente y de nuevo, gracias!!
Laura
Muy interesante el articulo, Francis. Lo que queria dar a entender en la conversacion por Twitter es lo siguiente:
1) Si por teoria de KK se entiende una teoria resultado de compactificar una teoria de gravedad pura en dimension mayor que cuatro, entonces esta claro que se ha abandonado, pero no en 1985, sino muchisimo antes.
2) En la jerga de la fisica moderna, las tecnicas de KK se refieren simplemente a la compactificacion de teorias de campos usando el formalismo de Scherk-Schwarz, que es un refinamiento de KK original. El formalismo de Scherk-Schwarz es muy usado en la fisica teorica actual y en concreto en teoria de cuerdas, y por supuesto no ha sido abandonado. La motivacion es no obstante diferente a la original de KK de obtener todas las interacciones elementales a partir de gravedad pura en dimensiones superiores.
3) La compactificacion de Teorias de Supergravedad tampoco se ha abandonado, todo lo contrario. La principal razon es porque cuando se dice que se compactifica una Teoria de Cuerdas uno se refiere usualmente a la compactificacion de la correspondiente Supergravedad, que es lo que se sabe (y no siempre) compactificar. Ademas, la Supergravedad contiene el espectro relevante para fenomenologia de la Teoria de Cuerdas, con lo que tiene sentido restringirse a ella. Notese tambien que la Supergravedad puede incorporar infinitas correcciones de la Teoria de Cuerdas y seguir siendo una Supergravedad. Por tanto, se siguen usando las tecnicas de KK refinadas en lo que se conoce formalismo de Scherk-Schwarz y es en este sentido por lo que sostenia que KK no se habia abandonado. El impetu que han recibido este tipo de compactificaciones de Teoria de Cuerdas (es decir, de la correspondiente Supergravedad) ha sido enorme gracias al interes de embeber en Teoria de Cuerdas duales gravitatorios relevantes y en obtener vacios de tipo dS.
4) Teoria de Cuerdas y Supergravedad estan siendo reformuladas en base a una nueva herramienta matematica, Generalized Complex Geometry y Exceptional Generalized Complex Geometry, que permite una descripcion mucho mas natural de la Supergravedad incorporando propiedades exclusivas de Teoria de Cuerdas (como la T-dualidad) y que permite un analisis mas profundo de las distintas compactificaciones, no disponible previamente.
5) Compactificar en algo que no sea una variedad diferenciable no es un problema, y personalmente no veo que haga perder belleza a la teoria. En Teoria de Cuerdas se compactifica muchas veces en variedades algebraicas (algebraic varieties, no confundir con manifold aunque sea la misma palabra en castellano) que genericamente contienen singularidades.
6) La Supergravedad en 11 dimensiones es mas importante que nunca, ya que es el limite de bajas energias de la Teoria M. La formulacion usando EGCG de la Supergravedad 11 dimensional puede ser el primer resultado de la Teoria M que va mas alla de la propia Supergravedad.
7) «La segunda razón por la que en 1985 se relegó a un segundo plano la idea de la supergravedad N=1 en D=11 fue que la compactificación de las dimensiones extra introduce una constante cosmológica enorme, proporcional a la masa de Planck al cuadrado;»
No estoy seguro de que esto sea correcto. La compactificacion de N=1, D=11 a 4 dimensiones en general produce un potencial escalar, y el minimo de dicho potencial puede ajustarse casi como se quiera siempre y cuando de lugar a un vacio AdS. De hecho es muy sencillo compactificar Sugra en d=11 a una sugra en d=4 sin constante cosmologica!. Lo dificil es lograr un vacio dS estable y demas: tal problema fue solucionado por KKLT.
8) Finalmente, decir que se ha comprobado que la Sugra N=8 en d=4 es finita a 4 loops y que hay argumentos muy fuertes a favor de la finitud a todos los loops. Dejo referencias con calculos explicitos, no charlataneria:
http://arxiv.org/abs/arXiv:1103.4115
http://arxiv.org/abs/arXiv:1104.5480
Notar de pasada que se ha comprobado explicitamente que la Teoria de Cuerdas es finita a dos loops solamente y hay argumentos sobre su finitud a todo loop.
Un saludo y disculpas por la longitud de la respuesta.
Respecto al punto 1, no es asi si por KK entendemos unificar los campos gauge del modelo estandar como parte de la metrica de gravedad en dimensiones extra, esto es, lo mismo que en los modelos de Kaluza y de Klein para el electromagnetismo. Con esta definicion, el rango de publicaciones va de 1981 a 1986 approx, encajando naturalmente con todo lo que se ha aprendido sobre compactificacion durante la decada anterior.
El ultimo articulo con contenido nuevo en esta linea de investigacion fué, diria yo, «Kaluza-klein Theories In Twelve-dimensions» de D. Bailin y A. Love, publicado en el 85.
Yo ademas de por el comportaminento de herding que siguió a la revolucion de cuerdas, voto por la tercera razón. La primera es inexistente. El articulo que la mayoria aduce como motivo para dejar de investigar los modelos con D=11 Kaluza-Klein fue precisamente, si miras las citas y cronologia en SPIRES, el que desencadeno esa investigacion: Realistic Kaluza-Klein Theories, de 1981, por Witten. En esos momentos el articulo sumaba a lo que ya se sabia de supergravedad, no restaba. Se hablo de la coincidencia de que la dimension maxima de supergravedad fuera tambien la minima para obtener simetrias SU(3)xSU(2)xU(1), y salto mucha gente al barco, ignorando que las ultimas paginas del articulo pudieran interpretarse como un non-go theorem.
Hay quien se da cuenta de esa anomalia y prefiere citar una extension de esa parte del articulo, que sí que tiene formato explicito de articulo de non-go, y que Witten presentó en Shelter Island II. Lo curioso es que los contenidos de esa presentacion a congreso no se incorporaron a ningun otro articulo y tuvo poquisima difusion, tan solo esta reimpreso, que yo tenga a mano, en un libraco carisimo, «Modern Kaluza-Klein Theories». Asi que me huelo que muchas citas a este articulo son de oidas, o de segunda mano a traves de los seniors que estuviendo en Shelter II. De hecho, vete a saber si los statements en la charla en directo fueron incluso mas contundentes que los publicados.
Ojo, no quiero decir que no existan esos teoremas de non-go, que ahi estan. Lo que pienso es que no pudo ser una razón historica para el abandono de la idea, porque si miras a la bibliografia fue todo lo contrario, fue el desencadentante de una gran oleada de investigación. Antes de «Realistic KK», todavia habia quien confundia la variedad compacta con el propio grupo de Lie, una confusion logica porque con una sola dimension extra U(1) tiene la misma topologia que S1. Witten abrio la puesta a pensar en terminos de isometrias y el formato de «non-go» de sus teoremas estaba pensado de forma constructiva, para investigar formas de evitarlos.
Visitando las carpetas, encuentro algunos papers de dificil acceso en la red, o que no es obvio donde buscarlos. El famoso non-go de Witten es «Fermion Quantum Numbers in Kaluza-Klein Theories» y dice lo que mas o menos sabemos, que Rarita-Schwinger compactificado en un espacio homogeneo produce una teoria donde los fermiones tienen numeros cuanticos «vertor-like». Eso es el abstract. Para todo lo demas, mastercard ($200 pavos el libraco de Appelquist) o tirar de fotocopias. Aunque avisa de que más alla de espacios homógeneos no se ha conseguido probar la imposibilidad, en general el tono es bastante pesimista.
La puntilla es «On SU(3)xSU(2)xU(1) Invariant compactifying Solutions to 11-Dimensional Supergravity», preprint ICTP 1623/84 de S. Randjbar-Daemi, Abdus Salam y J. Strathdee. Seguramente se puede encontrar en el archivo de preprines escaneados en KEK, o en algun catalogo del ICTP. Son contundentes: «none of these spaces can account for the SU(3)xSU(2)xU(1) quantum numbers of even a single generation of quarks and particles» Y rematan: «This is in addition to the well known chirality difficulty». La fecha es Febrero de 1984.
No obstante, en Noviembre del 84 David Bailin y Alex Love mandan un paper al Nuclear Physics B (NPB 254, 1985, p 543-554), «Kaluza-Klein in twelve dimensions», en el que afirman que desde esa dimension puede solucionarse la objeccion de Salam.
Por cierto, el paper siguente al de Bailin-Love en el NucPhys B es uno de Bagán, Latorre, Pascual y Tarrach sobre condensados de gluones.
Mientras se enfria el pure, aprovecho para añadir a este cocido un par de referencias no tan necesarias pero que se tarda en encontrar. Primero, «A classification of compatifying solutions for d=11 supergravity», de Castellani, Romans y Warner, NucPhysB 241 (1984) p 429-462. Dicen que ellos dan «a list of all homogeneus 7-manifolds». Es curioso que el review posterior de Duff se salte el «all», quizas Pope no estaba seguro de algo. Luego diez años mas tarde un grupo de matematicos (Nikonorov, Rodionov y Slavskii) cae en el tema de forma independiente -siguiendo a la escuela de W. Ziller- y encuentra un caso en el que se pude producir otra metrica de Einstein sobre la misma topologia, pero aceptan que la clasificacion de Castellani et al estaba practicamente completa.
Segundo, los teoremas de Massey y Kuiper, que tambien descubrio simultaneamente Arnold (asi que Atiyah lo llama de Kuiper-Arnold-Massey), sobre la relacion entre la 4-esfera y el espacio CP2. No veo de donde fotocopié el de Kuiper, su titulo es «The quotient space of CP(2) by Complex Conjugation is the 4-Sphere». El de Massey, en Geom Dedic v 2 (1973) pg 371, es exageradamente similar «The quotient space of the complex projective plane under conjugation is a 4-sphere». Casi casi difieren solo en el uso del articulo. Es posible que los dos oyeran el enunciado a partir de Arnold. En cualquier caso es importante porque la diferencia entre sacar SO(8) o sacar SU(3)xSU(2)xU(1) me da a mi que es simplemete si la variedad es un fibrado con base en S4 o en CP2. Y la operacion de complex conjugation podria ser la pieza que falta para resover el problema quiral.
Hola Francis. Buen post, como nos tienes acostumbrados. :).
Varios apuntes al respecto de todo esto, que creo pertinentes:
1) Approaches o «caminos» hacia la unificación de las fuerzas. En el post «sui generis» número 100 de mi blog (recientemente actualizado, aunque tengo detalles cosméticos y formales que resolver antes de volver a postear) ya hablé de ellos de pasada. Originariamente, si volvemos hacia atrás en el tiempo, en el siglo XIX y principios del XX conocíamos esencialmente sólo dos tipos de fuerza. Electromagnetismo (electricidad y magnetismo) y gravitación. Los intentos de Faraday (los hizo, creo recordar que hay un dibujo al respecto por ahí tipo «tira cómica» que siempre me encantó) fracasaron (a la hora de encontrar una inducción gravitacional electromagnética o similar inducción electromagnética gravitacional). Además, la constante de Coulomb es tan grande comparada con la gravitacional que es incluso sorprendente que pese a todo, formalmente, las leyes se comportan exactamente igual: leyes del inverso del cuadrado. Pero ahí para todo (aparentemente). Con el descubrimiento de las fuerzas nucleares (esencialmente el fenómenos de la radioactividad, y el descubrimiento de la estructura del átomo, sumado al de partículas subatómicas «sorprendentes») cambió el panorama de la unificación de las fuerzas. Posiblemente, Einstein fracasó en tu teoría unificada por ignorar el átomo, aunque posiblemente se verán sus intentos de buscar una teoría unificada del electromagnetismo o la gravedad como interesantes y pioneros dentro de unos siglos. Las idea de Kaluza-Klein originariamente fueron motivadas por la primera ruta hacia la unificación que comentas, Francis, es decir: todo es geometría y gravedad pura en dimensión superior es equivalente a gravedad más gauge. Es interesante destacar que esto ocupa solamente el nivel de bosones, pero no el «sector de materia». El interés de A. Einstein en las gravedades con torsión, la gravedad con métrica no simétrica o incluso teorías como el teleparalelismo distante se motivaron con la preconcepción de Einsteins de que TODO campo era algo geométrico. Esenciamenlmente la idea sería:
Idea A) Gravedad+Electromagnetismo (EM) -> Gravedad pura en dimensión 5
Idea B) Gravedad+EM-> Tensor métrico no simétrico, gravedad con torsión, teleparalelismo.
Idea C) Gravedad+EM-> Geometría
Idea D) Gravedad+EM+ «materia»-> Gravedad con torsión y sus generaliciones.
En resumen, el programa de Einstein, seguía a raja tabla el programa Erlangen. Sin embargo, es curioso que Einstein criticó inicialmente la idea de «campo gauge» (no creo que al final de sus días pensara que estaba mal) e incluso variaciones de sus propias ideas como la gravedad de Einstein-Cartan. El problema de este programa geométrico es que la gravedad es algo muy diferente al resto de fuerzas como el electromagnetismo, al menos, como Einstein mismo la concibió. Y yendo más allá de su teoría, en dimensiones superiores hay invariantes geométricos más allá del escalar de curvatura cuyos coeficientes no pueden ser determinados fácilmente. De hecho, hoy sabemos que los invariantes geométricos de teorías gravitacionales crecen sin control según aumenta D. Sin embargo, algunos principios los reducen, pero siguen siendo muchos más términos. En D dimensiones, la teoría más general que produce ecuaciones de segundo orden, consistentes con el principio de equivalencia y la covarianza generala, son las teorías de Lanczos-Lovelock (estudiadas en los últimos tiempos por Padmanabhan y la escuela chilena, en particular, pero también por gente como A. Chamseddine, cofundador de la geometría no commutativa junto a Connes).
2) La existencia de las fuerzas nucleares (de corto alcance) complicó el enfoque geométrico de KK, así que se mantuvo en la nevera hasta la supergravedad de finales de los 70 y principios de los 80 y 1982, con la primera revolución de las supercuerdas (la del cuarteto de Princeton). En ese momento, históricamente hablando, se recuperaron y modernizaron las teorías de KK. Sin embargo, las teorías con objetos extensos fue criticada por el asunto de la simetría conforme que aparentemente pierden. Ese asunto de la invariancia conforme, aparece en el libro que cité y citaste, Francis, de Supercuerdas: ¿una teoría del todo? de Alianza Editorial. Los teoremas no-go son famosos incluso en la historia de SUSY: la simetría de bosones y fermiones no podría lograrse solamente con conmutadores en la matriz S, pero si se relaja la exigencia a que existan generadores espinoriales, es posible tener un grupo de simetría que contenga tango el grupo de Poincaré como el grupo de simetrías internas, que es lo que uno esperaría tras el descubrimiento de las fuerzas nucleares y su descripción como teorías gauge (finalizado en los 60, no sin duros esfuerzos, como teorías YM no abelianas para la interacción débil y la fuerte). El asunto es que la simetría conforme en objetos como membranas o p-branas (p=2 o más , p=1 es cuerdas y p=0 son puntos) es algo delicado, no creo que ni siquiera esté comprendido hoy día pese a que se entienda que el grupo de infinitodifeomorfismos de transformaciones que respeten el p+1-volumen de las membranas sea algo que algunos tomen como mantra.
3) El renacer de las teorías de KK vino a finales de los 70 con la supergravedad y la teoría de Cremmer-Julia-Scherk, junto al mecanismo de Scherk-Schwarz que se usa aún hoy en teoría de (super)cuerdas. Lo que se abandonó, y esa es mi impresión personal, fue, a finales de los 80, salvo por un reducido grupo de personas que siguieron estudiando las membranas y objetos de dimensión superior, fue la idea «naive» de recuperar el Modelo Estándar como «compatificación espontánea»/»reducción dimensional» de una teoría de forma más o menos «única». No sólo es el asunto de la quiralidad, Francis. Las condiciones que uno usa para reducir dimensionalmente y obtener algo que se «parezca» al Modelo Estándar se pensaba que eran muchas menos. De hecho, la primera revolución de supercuerdas (podemos discutir si fue en 1982 o en 1984) fue el hecho de la cancelación de las anomalías permitía tener teorías de supercuerdas consistentes solamente con grupos gauge $latex E_8times E_8$ y $latex SO(32)$, las famosas cuerdas heteróticas (curioso nombre que ya apenas se usa, me refiero al de «heterotic»). En todo esto, Witten ya había «clasificado» o identificado el framework general de una teoría KK para un grupo gauge no abeliano general. Esto lleva al segundo camino en la unificación:
Idea A’) Unificar las teorías gauge bajo un grupo de simetría interna común, que contenga el grupo del Modelo Estándar electrodébil ( recordemos que las corrientes vectoriales neutras , modelo de Glashow-Salam-Weinberg de 1968, se «descubrieron» en los 70, y el nobel fue en 1979 para ellos).
Idea B’) Unificar con gravedad las teorías gauge «a la KK», en un set-up geométrico grupo teórico. La pista fue el hallazgo de la fórmula de Veneziano y su descripción relativista por Nambu como una cuerda. Scherk y Schwarz hicieron el resto e iniciaron la teoría de cuerdas moderna a finales de los 70. La idea de cuerdas parece contener no sólo campos gauge, sino también al gravitón (campo de spin 2).
En síntesis, dos rutas posibles para la unificación:
A) Gravedad+EM+ (Restos de fuerzas) +( Sector de materia) «tipo geometría pura». El sueño de Einstein y supongo que el del programa Erlangen, de geometrizar la física como «simetrías». También podemos ver que el enfoque de Loop Quantum Gravity y del old Canonical Quantum Gravity es precisamente seguir esta ruta con la variante de que cuantizar la gravedad puede hacerse con variables no triviales (los loops).
B) EM+ Campos gauge (corto alcance)+Gravedad+(Sector materia)-> Modelo de cuerdas, teoría M, supergravedad.
Comentario: la inclusión de materia en el enfoque A usual es un problema que se intentó solucionar con torsión y cosas tipo conexión de spin. Sin embargo, el método A, en el enfoque loop, ha demostrado también la importancia de SUSY para la inclusión de materia en teorías geométricas (y sin embargo SUSY no aparece…todavía). En el enfoque B, la inclusión de SUSY solucionó no sólo el problema de la inclusión de materia sino, también, la eliminación de modos (campos) taquiónicos en la teoría de cuerdas original.
Estas dos rutas tienen una diferencia adicional, y es en cómo surge la idea de «cuantización». En cuerdas, y en general en la mayor parte de los approaches de A) salvo el enfoque de Loop QG, la cuantización es algo primario, y las ecuaciones de Einstein se obtienen como aproximación de baja energía, bien de cuerdas en alta dimensión o de alguna supergravedad. La teoría M sabemos que tiene a nuestra «vieja amiga» SUGRA máxima en D=11 como aproximación de baja energía, pero nadie sabe aún cómo cuantizar un objeto como una membrana (P=2) o una 5-brana (su dual). Es posible que se necesite un profundo conocimiento de las estructuras n-Lie algebraicas y la mecánica de Nambu extendida para solucionar el problema, pero no es para nada trivial. Si lo fuera, ya estaría resuelto y tendríamos tando predicciones «nuevas» como posiblemente algún criterio para poder «falsar» la teoría M (si resulta que su escala de energía no es la de Planck). Mi impresión es que no comprendemos aún casi nada del régimen no-perturbativo de teoría M, ni sus grados de libertad fundamentales (sugra en D=11 tiene 2-branas y 5-branas como fuentes, pero de nuevo no sabemos cuantizarlas). La propuesta de Banks de que M-theory es describible como una teoría de «matrices grandes», hecha de D0branas, es algo que hasta la fecha sigue siendo una conjetura indemostrada. También es destacable, que J.A. de Azcárraga et. al. (ahora presidente de la RSEF y emérito) propusieron usar BPS «preons» como los grados de libertad fundamentales de M-theory, usando supertwistors y tensorial (twistor-like) superspaces como los elementos fundamentales de la teoría. Hubo cierta crítica (fundada) respecto de ese approach, pero finalmente tampoco se ha desarrollado mucho más. En síntesis, M-theory (y superstrings, por extensión) ha llegado a una vía muerta de donde no se sabe por donde seguir (unos, como West, han propuesto ir más allá y usar el álgebra $latex E_11$, no lineal e infinitodimensional, origen de hecho de las teorías «double field theory», O(D,D), que están ahora «de moda»…). Esta frustración parcial ha llevado a reenfocar lo aprendido con las D-branes en cosas como la materia condensada o el confinamiento de los quarks (sí, volvemos a los 60, con Veneziano y los modelos duales, justo como el asunto de los firewall nos ha hecho retroceder a tiempos originales de BH explosions).
4) El asunto de las modelos de membranas, que si nos lo tomamos en cuestión de «patente» se debe al propio P.A.M. Dirac, no bajó pese a la crítica de los stringers a finales de los 80. Duff, Pavsic, y varios otros trabajaron en modelos extensos que llevó a la dualidad en el 95. Así que, irónicamente, las membranas se «vengaron». Y eso alteró la forma de ver todo. De hecho la idea de holografía, motivada por ‘t Hooft y Susskind para evitar la BH information paradox, encontró en la idea de dualidad refugio. Y en ese caldo de cultivo surgió la dualidad AdS/CFT (via Maldacena, y su famosa canción que rima con la Macarena, jejej), así como la dualidad genérica gravity/gauge. Los útiles de KK y las diferentes formas de reducción dimensional no se han abandonado, sino que sean incorporado a los diferentes modelos y teorías actuales. De hecho, el problema de la quiralidad, esencial como comentas Francis, es un problema que puede solucionarse con condiciones de contorno cuando reduces o compactificas la teoría. Por supuesto, hay problemas: no hay forma unívoca de hacerlo, en ocasiones no puedes acomodar los campos sin ciertas hipótesis adicionales, y está todo el asunto de los moduli y otros campos que aparecen (generalmente sin control total) en la escalera de la reducción dimensional. Al final, el resultado es que debido a los compactificaciones y el flujo inducido por los moduli, no hay una manera única de lograr que M-theory-> Poincaré más grupo del Modelo Estándar. En retrospectiva, hemos perdido la capacidad de predecir algo más allá de decir:hay tantos campos escalares extra, tantos campos gauge adicionales, el gravitino, el gravitón, resonancias KK o similares. El enfoque sin embargo es autoconsistente, pues contiene gravedad cuántica (se supone que finita aunque no está demostrado aún para N=8, D=4 sugra aunque para D=11, N=1 la teoría es no renormalizable, está conectada a las teorías de cuerdas por dualidades y a M-theory- puede verse simplemente por dualidad con cuerdas si no queremos más que algo conceptual). Sin embargo, el problema sigue siendo que no hay predicciones de por qué la teoría o el modelo estándar tiene 3 generaciones, por qué las masas o cargas deben ser los que son, y el asunto de los mixing o las violaciones de C, P, y T, o a pares, permanece siendo un absoluto misterio con M-theory. M-theory es lo mejor que tenemos, matemáticamente hablando, pero siendo críticos, es una teoría que no está aún bien definida, ni comprendida. Y desde 1995 han pasado casi 20 años… El landscape+ el problema del moduli (o las compaticiones de flujos) siguen siendo sin duda uno de los argumentos de más peso para criticar una teoría cuyo éxito es, atención, fundamentalmente matemático y unificador, pero hasta ahora, poco empírico: da igual que sus métodos hayan servido para calcular cosas difíciles en lattice QCD, o en física de agujeros negros, o que tenga en su haber gran parte de las matemáticas (no todas) más importantes de finales del siglo XX y de inicios del XXI: geometría diferencial , fibrados, grupos excepciones, supergrupos, análisis de Fourier y teorías KK, álgebras de Clifford, super Lie groups, cohomología, topología, métodos no perturbativos, teorías de campos conformes, twistors y supertwistors… Experimentalmente hablando, sólo tenemos un higgs (mínimo y neutro) de 127 GeV. Y no demasiadas pistas sobre dónde está la Nueva Física (tipo libro de P.C.W. Davies, the New Physics) salvo por toda esa dark matter y dark energy que las observaciones cosmológicas apuntan que están ahí, esperando a que las descubramos aquí en la Tierra…
Como epílogo, me gustaría comentar que la dualidad gauge/gravity puede estar diciéndonos incluso que la gravedad y los campos no son «fundamentales» sino nociones complementarias o duales (como en otro tiempo lo fueron ondas y partículas, que hoy entendemos como dualidad en términos de su emergencia del concepto de «campo»: campo/ondas/partículas es en realidad un trialdad). Ahora, entender qué es el tercer miembro de la dualidad gauge/gravity es también simple, debe ser algo «fundamental». Si ondas y partículas son manifestaciones de los campos, los campos gauge y la gravedad son en si mismos duales a la idea de gauge/gravity/geometry, así que la cuestión esencial es simplemente, lo que entendemos por campo/geometría. Esa y no otra es la cuestión subyacente a todo… Por supuesto los campos existen, como la geometría, pero ¿qué es un campo? ¿Qué es geometría?¿Qué significa cuantizar la gravedad? Ésa y no otra también es la pregunta que hay tras la preguna ¿qué es string theory/M-theory?¿Debe la gravedad cuantizarse o clasicalizarse los campos cuánticos de alguna forma exótica? No entedemos su geometría fundamental, ni sus grados de libertad. Hay intentos de formulaciones no perturbativas de M-theory, como Matrix Theory, $latex E_{11}$, y otras construcciones, pero están aún en pañales. Sin embargo, sabemos que como teoría cuántica, M-theory está bien definida desde el 95, pero no sabemos lo que es más que por teorías efectivas, y no hay demasiados principios que nos ayuden como ayudaron a Einstein el principio de equivalencia, la covarianza general y el principio de relatividad. De momento, parece que vamos a ciegas…O casi…Pero es una aventura fascinante.
Addendum: Los enfoques A y B han confluido «más o menos» hacia SUSY. Eso lleva un problema no menor desde la perspectiva experimental actual, y hablo del LHC y de sus sucesores. Hay que encontrar SUSY. Si no encontramos SUSY (y ojo, Alejandro es excepcional en el sentido que el piensa que SUSY está ya presente en el Modelo Estándar que conocemos) eso tira M-theory y supercuerdas, pero también los enfoques de loop que incluyan SUSY. Leí una vez un paper titulado como SUSY without SUSY o algo así…En este espíritu. Nótese que hay teorías de cuerdas NO supersimétricas, así como hay teorías GUT no supersimétricas también. Aunque, en mi opinión, se está fiando todo a la idea de SUSY…Y es una apuesta realmente fuerte y peligrosa.
Addendum (II): Encontrar SUSY siempre ha sido uno de los objetivos de LHC, o más bien, siendo realistas, explorar el espacio de parámetros del MSSM y otros modelos supersimétricos no estándar. El problema es que la Naturaleza sigue dando la razón tanto al Modelo Estándar como a algo que se le parece mucho. Y eso es notable. Como dice Frasca en su blog, el SM se ha mostrado «irrompible» (unbreakable), tanto como la General Relativity/relatividad general se mantiene inmutable tras casi un siglo, pese a los pensamientos de que es una teoría efectiva como el SM, sigue ahí…¿Por cuánto tiempo los datos seguirán apoyando estas dos excepcionales teorías? ¡Quiero más anomalías! ¡Quiero datos! Y espero que en los próximos años, podramos elucubrar y trascender estas dos teorías por algo aún mejor, y que incluirá la dinámica de materia y energía oscura, y sus posibles interacciones.
Hola amarashiki. Puedes explicar por favor tu siguiente frase «álgebra E_11, no lineal e infinitodimensional, origen de hecho de las teorías “double field theory”, O(D,D), que están ahora “de moda»? Como es E_11 origen de la double field theory?
Vete al arxiv y mira los papers de West, o su reciente libro de SUGRA (yo le poseo). La idea de que el grupo de dualidades de sugra en d=11 y el hallazgo de $latex E_{11}$ se debe a su grupo de investigación y a varios tipos de la escuela ruso-soviética que siguen dando «guerra». El álgebra de $latex E_{11}$ generaliza la idea de SUSY realizando dicho álgebra de forma «no lineal». Es decir, dicho álgebra (infinitodimensional) es una non linear SUSY. Usando este álgebra, puedes redefinir los grados de libertad gravitacionales de la teoría en 11d usando simplemente dos campos relacionados por dualidad T. Creo que la referencia es E_11 in M theory o algo así…Dicho paper, y si quieres las teoría F (una teoría en 12 dimensiones con 2 tiempos) y la two-time physics de I. Bars están en la genésis de lo que ahora se llama «double field theory», un área que se enmarca la idea de comprender y generalizar el grupo de U-dualidad en supergravedad maximal.
Los papers que citas arriba de R. Kallosh son importantes, pero la verdadera revolución ha sido el uso de técnicas twistoriales para calcular las amplitudes a varios loops en sugra (tanto en alta como baja dimensión). De hecho, lo sorprendente es que lo que mantiene finita la teoría de supergravedad usando dichas técnicas no parece que sea precisamente supersimetría. Las amplitudes y recientes fórmulas de Cachazo y Skinner han arrojado luz sobre la finitud de SUGRA pero lo que mantiene finita o anula algunas amplitudes es actualmente desconocido (pero se sabe ya que NO es SUSY ¡!) en dicho enfoque twistorial.
Como curiosidad, he apostado contra un experto en SUGRA, que ha estado trabajando con R. Kallosh, que no creo que se demuestre la finitud de SUGRA N=8 en menos de 4 años…Demostrar la finitud de N=8 SUGRA es un handicap, podría ser un broche para la carrera de Renata, pero no hay forma aún de convencer a nadie de que perturbativamente ciertas amplitudes se cancelarán…
Por cierto, ¿sabes lo que es $latex E_{11}$ y cuál es su álgebra y sus propiedades?
Hola amarashiki. No has respondido a mi pregunta. Decir que E_{11} «esta en la genesis» de double field theory y traducir el abstract de hep-th/0104081v2 no pued considerarlo una respuesta; buscaba algo mas especifico. El libro de West lo conozco, y me gusta bastante, pero ahi no viene la respuesta a mi pregunta (que yo sepa). Tambien conozco por encima la idea que hay detras del E_{11} y su papel en ST/Sugra, pero jamas habia visto que E_{11} fuera el origen de la double field theory ni similar. Puedes indicarme la referencia al respecto concreta, o en que parte del libro de West se comenta tu afirmacion?
Por cierto, personalmente yo no diria que la double field theory pretende «generalizar» o «comprender» el grupo de U-dualidad de la sugra maximal. Primero porque ya estan comprendidos y clasficados, y segundo porque el grupo de U dualidad es el que es (esta demostrado matematicamente) y no se puede modificar o «generalizar» en Sugra, y menos maximal. Lo que pretende DFT es incorporar la accion de T-duality (que surge con cuerdas), a los campos massless de la cuerda doblando el numero de coordenadas.
Creo que estás bastante equivocado, Kac…Sí que te he contestado, y con poco que hubieras mirado oportunamente, encuentras la respuesta a tu pregunta. Te puedo decir que no lo he hecho, porque yo mismo leía los papers de West en tiempos de la Uni cuando me escapaba de mis aburridísimas clases de óptica o electrónica…Así que obviamente, algo recuerdo de aquello, porque algún paper me imprimí y tengo perdido en alguna de mis carpetas, que acabo de consultar…
Hombre, traducir un abstract ¿realmente te ha parecido que he hecho eso? Yo he trabajdo en esas cosas, y algunas cosas de SUGRA (by my own, of course, unfortunately), así que he tirado de memoria (que tengo, y bastante…) bastante más avanzadas o podemos decir «in the edge».
Sobre el asunto del double field theory, pareces que tienes unos conocimientos limitados a la traducción de la wikipedia…
Sobre el grupo de dualidad, en sugra las U-dualidades están clasificadas, sí, es cierto…Pero como sabrás, supongo, es que se busca la compleción ultravioleta de SUGRA. Y se espera, que la compleción UV de SUGRA arroje pistas sobre nuevas simetrías y los grados de libertad fundamentales (y estructuras como las que comentas, sorprendemente aquí en twitter sin exhibir para nada su dominio in situ de ellas) de la teoría (hoy desconocidos) M. La idea de que gravedad es una especia singular de «copia» de una teoría gauge con simetría rota muy particular, tipo (non-linear) sigma model, me lo comentó el mismísimo Frank Wilczek en mi twitter hace poco tiempo, supongo sabes quién es Wilczek, ¿no? Supongo que sí, porque parece que te gusta fardar de lo que sabes pero no te gusta reconocer lo que otros conocen. Este hecho de interpretar la gravedad como cierta teoría gauge (y no, no es cierto lo que decías en twitter sobre que gravedad es una teoría gauge. No es una teoría gauge en el sentido normal, porque no hay álgebra de Lie que satisfaga la relatividad general en su formulación mínima. Hay una estructura diferencial que «sugiere» una teoría gauge, pero en vez de un constantes de estructura hay funciones de estructura no constantes. Y eso, estimado Kac, no es un álgebra Lie. Otra cosa muy diferente es que reformules la gravedad en otras variables e identificando objetos, crees algo similar a una teoría gauge pero sólo lo es en apariencia. La conexión de una teoría gauge está definida en un fibrado principal en un grupo de Lie, mientras que la conexión asociada a la gravedad está asociada al espacio-tiempo mismo. Los grupos de Lie son compactos, el grupo de simetría de relatividad asociado al espacio tiempo es el grupo de Poincaré, que no es compacto…La analogía funciona a nivel formal bien, pero la forma en que la gravedad ES una teoría gauge NO está para nada entendida. Por supuesto, está muy bien que teoría de cuerdas permite contar estados vía representaciones del grupo pequeño y campos via teoría de las representaciones de grupos, pero insisto en este punto. De hecho, el revival de los últimos años en gravedad masiva se debe, entre otras razones, a los esfuerzos por comprender mejor la ruptura de simetría asociada al grupo de difeomorfismo en relatividad general, a la gravedad linearizada tipo Pauli-Fierz masiva, y al mecanismo de «Higgs» en el contexto de gravitación (del que han derivado los trabajos de modelos de campos escalares llamados Galileones).
Como bien dices arriba, SUGRA se sabe ya que es finita a 4-loops, aunque más precisamente, por dualidad con N=4 SYM y contaje de contratérminos (¿sabes lo que es un contratérmino? No esquives la pregunta como lo has hecho con E(11): ni me has mostrado su álgebra, ni me has dicho si sabes lo que es y digo una definición que no esté en libros, pero que requiere simplemente una línea; para alguien que se ha jactado públicamente de que otras personas estaban confundidas y cometían errores, tú has cometido unos cuantos, espero no me hagas citarlos pues parece que te gusta criticar a los demás pero no te gusta que te critiquen a ti) se sabe algo más a fecha actual. Se sabe que la presencia de divergencias a menos de 7 loops parecen MUY improbables ( Dixon y su grupo, junto a Cachazo, Skinner y otros, y Frascatti et. al.).
Acabo de consultar lo del Paul West…Haciendo un par de clicks via paul west en arxiv, se puede encontrar dónde surge lo del double field theory (y sí, surgió de él, aunque el nombre se debe a Hull y Zwiebach,e que empezaron hace 4 años o así con eso). En realidad, si haces un trackback, el hilo de double field se ramifica en la idea del E(11) y en la two-time physics de Bars, la geometría de twistores y no sólo en la cuestión no menor de la clasificación completa de las dualidades en supergravedad.
Te animo a que lo intentes y no me pases la bola ( me recuerdas a otra persona que tenía esa mala manía de escurrir el bulto). Yo te he respondido correctamente, y te he citado (aunque no recordaba la referencia concreta que citaste arriba) de West, porque yo he calculado en dualidades «mis cosillas». En los trabajos de West, si te tomas la molestia de no leer meramente el abstract y haces una búsqueda más exhaustiva, está. De hecho, en ese mismo paper que citas está el germen de gran parte del asunto…Pero al parecer, no lo tienes demasiado claro.
Y ahora:
A) ¿Sabes lo que es E(11) y sobre todo de dónde sale exactamente? Y, por favor, no me vengas con otra pregunta absurda que puedes responder por ti mismo (búsqueda bibliográfica). Y me refiero a una definición, que no viene en ningún libro o paper sobre lo que es dicho álgebra. NO escurras el bulto esta vez, puesto que yo sí que te he respondido y tú a mí no a nada.
B) ¿Sabes lo que es un contratérmino y cómo se sabe que SUGRA N=8 es finita hasta 4 loops? Para ser más preciso se sabe que es finita a menos de 7 de loops, por contaje con la teoría SYM dual asociada y los cálculos que han hecho varios ( no precisamente a mano, en el caso de L=3 y L=4; Dixon y su grupo lo calculo en supercomputadoras).
C) ¿Sabes lo que es una teoría gauge o no? Porque parece que no tienes claro el concepto, y lo digo de verdad. ¿Eres físico?
Hola amarashiki. Gracias por tus respuestas. La gravedad es una teoria gauge ya que es invariante bajo un grupo local de transformaciones (el grupo de difeomorfismos). Lo que la gravedad no es, es una Teoria de Yang-Mills, ya que el grupo de difeomorfismos no es un grupo de Lie. Es decir, la RG es una teoria gauge pero no una Teoria de Yang-Mills. Es una cuestion de nomenclatura mas bien: una teoria gauge es una teoria invariante bajo un grupo local de transformaciones. Una Teoria de Yang-Mills es una teoria localmente invariante bajo un grupo de Lie (compacto o con los requisitos que se deseen imponer).
Por otro lado no voy a responder a tus inquisitorias preguntas porque no eres quien para examinarme de nada, y no tengo por que saber la respuesta a tus preguntas. De hecho me parece ridiculo que te pongas a examinarme, y no veo que fin puedes tener en mente: quieres probar que no se de que hablo? que sabes mas que yo? Ya te respondo yo encantado: seguramente sabes mucho mas que yo de Fisica, y por supuesto lo que digo lo digo desde mis escasos conocimientos y sin ser experto. Queda tambien claro que eres Fisico y que ya leias papers cuando estabas en la Universidad. Me has preguntado si soy Fisico. Aunque es una pregunta insidiosa, por la intencion con la que la haces, te respondo sin problema: no, no lo soy, y no creo que por ello mi opinion tenga menos peso si va suficientemente argumentada.
Por otro lado, lo que yo te he preguntado es una aclaracion sobre algo que tu has afirmado, lo cual SI procede en un debate (y no el examen al que me quieres someter). En estos casos, se suele dar una referencia concreta, y si la referencia es larga se suele indicar la pagina. Tu me has mandado a los «articulos de West» (que no son precisamente pocos). Como comprenderas no puedo ponerme a revisar todos sus articulos a ver en cual sale lo que tu afirmas. En el unico paper que has mencionado de West no viene nada que apoye tu afirmacion. Asi que si por favor conoces la referencia donde se demuestre o argumente lo que has comentado te agradeceria enormemente que me la comunicaras, ya que me interesa el tema (si no recuerdas la referencia pero si el argumento, me vale tambien una explicacion si tienes tiempo).
No creo que haya fardado de nada, solo he dado mi opinion, y si quieres que argumente o de referencias sobre cualquier cosa que haya dicho, lo hare encantado. Como no soy experto en estas lides, tambien es posible que haya cometido errores, como tu has indicado. Si es asi por favor dimelos para «subsanarlos» y de paso aprender. Al contrario de lo que indicas, no tengo ningun problema en ser criticado, asi que estare encantado en que numeres los errores en los que he caido para poder aprender de ellos.
A ver amarashiki y Kac, pienso que es evidente que esto no es un tribunal o un concurso académico, no se trata de demostrar quien tiene más o menos conocimientos sino de intentar producir un intercambio positivo de ideas u opiniones. Con todos los respetos (aunque quizás yo no sea a veces un ejemplo de diplomacia :D) pienso que si somos demasiado susceptibles y nos ponemos continuamente «a la defensiva» pensando que el otro nos quiere «avasallar» o algo por el estilo es muy difícil mantener un diálogo constructivo, y sería una pena porque es imposible encontrar una página en todo el país con comentaristas del nivel vuestro por ejemplo. Además ¿Qué clase de ejemplo estamos dando a los magufos y tarados conspiranoicos si nos peleamos entre nosotros? Luego empezarán a decir que si los científicos son unos soberbios egocéntricos, que si la teoría de Mariló :D. Supongo que al menos en alguno de mis argumentos estaréis ambos de acuerdo.
Parece como si fueramos vivtima de esos concursos de «clubs de debate» que se ven en las peliculas americanas y que puede que formen parte del sistema de educacion anglosajon; en mi colegio nunca tuvimos asignatura de debate, ni en la universidad. Y me alegro de ello, porque por lo que deduzco de las peliculas esa cultura lleva aparejada la sugerencia de que se puede defender una u otra idea indistintamente,
Sobre lo que es una teoría gauge, casi aciertas. Aunque te doy la razón, es un asunto de nomenclatura nada más. Pero en tu definición de teoría gauge falta diferenciar que la gravedad actúa sobre todo el espacio base de coordenadas, mientras que las teorías gauge o YM sólo actúan sobre el fibrado principal con base en el espacio-tiempo. Dicho de otra forma, el grupo de difeomorfismos actúa sobre todas las coordenadas sobre la que la gravedad y campos están definidos: el grupo de simetrías de la gravedad (llámalo difeomorfismos o como quieras GL(d,R) en su realización matricial más simple) cambia el punto del espacio tiempo bajo una transformación «gauge» (ojo, lo pongo entre comillas), de x a x’. En cambio, en una teoría gauge tipo YM las coordenadas de los campos en el espacio tiempo permanecen constante,sólo cambian localmente las coordenadas internas que definen los campos en el espacio tiempo (espero que no me hagas ponerte una transformación gauge abeliana o no abeliana para aclarar este punto). Bajo este punto de vista, queda claro que la gravedad NO es una teoría gauge usual (tipo YM). Ciertamente, esta cuestión posiblemente es cosa sólo de terminología. Hay teorías gauge que no son YM, ciertamente. Te podría citar unas cuantas que no son ni el SM ni GR o SUGRA, porque también las he estudiado (es lo que tiene tener novia esporádicamente y no tener muchas hobbies u ocupaciones más allá de dar clases para sobrevivir o estudiar día tras día desde 1999…).
O sea, dices que «(…)Por otro lado no voy a responder a tus inquisitorias preguntas porque no eres quien para examinarme de nada, y no tengo por que saber la respuesta a tus preguntas.(…)» y luego me pides que yo SÍ tengo que responderte a tus preguntas (de las que sé evidentemente las respuestas). Evidementemente, no es un trato muy justo y equitativo. No demuestras ser muy consistente, sólo, como te dije, bastante creido y prepotente. Como otra persona que adoptó esa actitud. Igualita, vaya.
Dices que no eres físico, pero te permites el lujo de señalar «errores» que no lo son y te arrimas a un lenguaje y afirmaciones que hay que tener muy claras para no meterse en berenjenales peligrosos. Simplemente te digo, que te pasas de la raya diciendo que cierto texto tiene numerosos errores, pero luego no citas ninguno y te empiezas a meter en el asunto de KK bastante peligrosamente y haces afirmaciones sumamente sospechosas sobre el tema de la geometría compleja generalizada y otras estructuras excepcionales que aparecen efectivamente en SUGRA. Por cierto, llegas a decir en cierto momento en twitter que las supergravedades no están clasificadas. Eso es evidentemente incorrecto. Están clasificadas desde hace bastante, otra cosa es que su finitud y renormalizabilidad pongan en duda su consistencia a nivel cuántico. SUGRA en d=11 no es renormalizable ni tiene una descripción cuántica a mano (aunque se han hecho varios intentos como el de West y otros grupos por aumentar sus simetrías más allá del grupo de dualidad U, como esto del double field theory y que tiene evidentemente motivaciones diversas, más de las que crees saber).
El argumento está en el propio artículo de West que te citaba (y con el que te he puesto a prueba, sí…¿Soy un capullo por querer saber el nivel y credenciales de con quién estoy discutiendo?Con Francis y otros varios lo sé, de mí es fácil tirar del hilo para saber quién soy, pero al parecer tú tiras balones fuera cuando se te pregunta incisivamente ¿te sienta mal?). Veo que no lees «entendiendo», lo cual es grave en cuestiones matemáticas (en física te puede servir para aparentar saber un poco, pero es fácil discernir quién tiene capacidad matemática y de lectura). Ojo, yo también en ocasiones cometo errores, leo bastante rápido (al menos todavía, veremos cuando empiecen a mermar mis capacidades, pero espero aún falten un par de décadas para eso) y en ocasiones me despisto, pero suelo prestar atención a las citas… En general, el argumento intuitivo es que si hay dualidad T sobre toda una teoría tienes una suerte de longitud mínima (podemos imaginar que sea la longitud de Planck o cualquier otra longitud fundamental no descartada mucho menor que el fermi, que es hasta donde hemos testado el SM) y por dualidad hay una especie de longitud máxima (puedes pensar en el radio de de Sitter-constante cosmológica disfrazada). Si ocurre esto con el espacio, también ocurre con el tiempo por la misma dualidad. Así que si tú quieres extender la noción de simetría T a todo el espacio tiempo y no sólo sobre la worldsheet, eso lleva de forma natural al doblaje de todas las coordendas de espacio-tiempo (creo que el artículo en el que lo cuenta West es 2003 ó 2004, lo tendría que mirar porque dejé esto por esa época, salvo lo relativo a funciones automórficas-en las cuales sigo interesado por diversas razones, no sólo por SUGRA-, que fue cuando me licencié y tuve que andar aún sobreviviendo dando clases en academias y tal mientras intentaba buscarme la vida para el tercer ciclo, ahora máster).
Nota: dices que no eres experto, pero te permite el lujo de citar artículos, decir que hay «errores» en un artículo y además señalas matemáticas que dudo comprendas (con todos mis respetos, si no las entiendo ni yo, y no soy manco en matemáticas profesionales) aunque tengo mis limitaciones porque no uso ni el Mathematica ¿lo sabías?Todo lo hago generalmente a mano o apoyándome ligeramente en wolframalpha free (sin licencia) desde hace algún tiempo, porque no he profundizado en ellas-técnicas computacionales-, dudo que tú sepas de lo que hablas más allá de citarlas. No se trata de dar referencias o citar.
Argumentar es fácil, pero entender es complicado y requiere tiempo en general, y más si no estás muy entrenado. Y estamos hablando de que un físico o matemático profesional calcula cosas «serias» sabiendo lo que hace (aunque muchas veces, incluso en nuestros blogs, especulamos como todos un poco «in the edge», hay una diferencia entre matemáticas serias y otras que son simplemente «engañabobos»).
Tus errores (más allá de una ligera discrepancia sobre lo que es una teoría gauge local que es menor y ciertamente nominal):
1) Comentas en twitter que las supergravedades NO han sido completamente clasificadas. Eso es totalmente falso. Aunque de nuevo, supongo que la cuestión es la nomenclatura. El propio Scherk estudió la hipergravedad en D>11, pero incluye campos de alto espín que se cree no son físicos o no son tratables no ya de forma supersimétrica, sino por cualquier teoría razonable gauge «usual». Una excepción moderna es la teoría de Vasiliev, por la que recientemente se han interesado los teóricos de cuerdas y supergravedad. No hablaré aquí sobre el problema de una teoría de campos interactuante de espín mayor que dos. Daría para demasiado y para estar toda la tarde hablando sobre por qué la teoría de Vasiliev ha pasado de ser una «aberración» y algo «feo», a algo que interesa…
2) Tienes problemas para entender el lenguaje en teorías Kaluza-Klein, y ciertamente te equivocas en ciertas «citas» históricas.
3) Te permites el lujo de decir (y te cito): «(…) Compactificar en algo que no sea una variedad diferenciable no es un problema, y personalmente no veo que haga perder belleza a la teoria. En Teoria de Cuerdas se compactifica muchas veces en variedades algebraicas (algebraic varieties, no confundir con manifold aunque sea la misma palabra en castellano) que genericamente contienen singularidades(…)».
Para empezar, ¿sabes qué es una algebraic variety y su diferencia con una manifold? para soltar este párrafo y quedarte tan «ancho» hay que ser muy cortito y limitado en matemáticas. Te pregunto. ¿Sabes que es una variedad algebraica?¿Y una variedad diferenciable? Te lo digo no como un test, para nada. Sino porque la cuestión de la diferenciabilidad (que ciertamente ciertas geometrías cuánticas tratan en variedades algebraicas) no está en tela de juicio, sólo la presencia de puntos singulares de las mismas. Si querías decir, compactificar en algo que no sea una variedad diferenciable NO es un problema per se es absolutamente falso. Las algebraic varietes son variedades diferenciables salvo en algunos puntos, PERO, ¿sabes que las variedades algebraicas SON «manifolds»? Porque parece que por lo que dices no sabes de su conexión. La presencia de puntos singulares en la variety no estropea la diferenciabilidad, aunque sí da problemas en las singularidades (que algunos han usada para modelar transiciones entre diferentes topologías como taza y una esfera, pero no puedo darte los detalles técnicos de ello por aquí, tristemente), en general las variedades algebraicas son también «manifolds» y diferenciables salvo en esos puntos «especiales o singulares». Decir que la no diferenciabilidad no es un problema es un craso error, puesto que no tenemos conocimientos de geometría (multi)fractal suficiente hoy día para saber qué pasa en tales casos (aunque si buscas, algunos se han atrevido a especular con espacio-tiempos y dimensiones fractales a diferentes niveles de sofisticación: desde Nottale hasta un tipo que anda paro el CSIC haciendo QFT en espacios fractales, pasando por otros varios que han hecho hasta cosmología «fractal» muy especulativa, y no hablo de Nottale, hablo de otros). Además, y perdona, pero no quiero ponerme demasiado crítico contigo, créeme, el problema es más bien el opuesto. Hay muchas variedades diferenciables que no son algebraicas en absoluto (en el sentido que supongo dices), un ejemplo son las superficies K3 o más generalmente sus generalizaciones en dimensión superior como son las variedades Calabi-Yau. Precisamente, uno de los problemas del «landscape» es que no hay forma de seleccionar la topología y geometría de la variedad sobre la cual compatificar. Y dado que hay transiciones entre las diferentes posibles geometrías, no podemos seleccionar ninguna. Como sabrás se habla de que hay hasta 10⁵⁰⁰ posibles Calabi-Yau… «Naive» KK se hace en hipertoros, porque es lo más manejable, pues nadie sabe aún no ya calcular las autofunciones sobre ciertos espacios, sino simplemente saber cuántos de ellos existen…Y ni te hablo si encima «quitamos la diferenciabilidad» como requisito. En parte, todo el enfoque de degravitación basado en espacios que son un retículo está basado en la idea de simplificar el asunto al igual que se hace en lattice QCD con los campos, aunque hay resultados ciertamente interesantes, tampoco ha habido una predicción que produzca el SM de forma única. Hay simplemente demasiadas formas de hacerlo.
4) Dices:»(…)La compactificacion de N=1, D=11 a 4 dimensiones en general produce un potencial escalar, y el minimo de dicho potencial puede ajustarse casi como se quiera siempre y cuando de lugar a un vacio AdS. De hecho es muy sencillo compactificar Sugra en d=11 a una sugra en d=4 sin constante cosmologica!. Lo dificil es lograr un vacio dS estable y demas: tal problema fue solucionado por KKLT.(…)»
El potencial escalar no sólo es un problema de la SUGRA, es un problema general de toda teoría de supercuerdas (el problema de los moduli). NO es verdad lo que dices que el mínimo pueda ajustarse como se quiera siempre y cuando de lugar a un vacío AdS (¡mentiroso!). Ahí te has vuelto a colar. El ajuste del vacío NO depende para nada de la geometría AdS. Hay formas de que SUGRA se reduzca a un vacío que no sea tipo AdS, que se selecciona simplemente porque con AdS tenemos la correspondencia y conjetura de Maldacena (que por otra parte sigue sin estar totalmente probada formalmente a nivel matemático) AdS/CFT, y las teorías conformes las sabemos manejar muy bien no sólo por cuerdas, sino porque son teorías de campo bastante manejables (en mi máster se estudiaban , aunque yo las conozco y he manejado desde el 2001 a nivel postgraduado) y un espectro que conocemos bien, los correladores de las funciones asociados a los campos conformes son conocidos, y otras propiedades interesantes que tienen (y que se han beneficiado de la propia teoría de supercuerdas).
Finalmente tu comentario acerca de que la teoría de D=11 SUGRA es más importante que nunca…Sí y no. Se sabe desde el 1995 (aunque las misteriosas cancelaciones de las anomalías ya las conocía Hawking antes de la revolución de Green-Schwarz de las supercuerdas), y por eso no es que sea más importante que nunca. Siempre lo ha sido. El problema de SUGRA es que sus grados de libertad fundamentales no son tratables con las técnicas de cuerdas dado que son 2-branas y 5-branas, y para esas cosas no podemos hacer trucos como el de Polchinski para la acción de Nambu-Goto (bueno, sí puede hacerse igualmente, pero no lo siguiente) porque con las membranas no tenemos que sean un conjunto infinito de osciladores armónicos de forma tan trivial (de hecho, en general, el espectro de la membrana en SUGRA sugiere que su espectro es «continuo» a no ser que hagas ciertos malabarismos matemáticos, con el consiguiente problema para estudiar la teoría) como hacemos con cuerdas. Sí es cierto de las geometrías excepcionales y geometrías complejas, pero eso se sabe desde mucho antes…
Además te diré otra cosa más. No me juzgues como insidioso. ¿Sabes lo que es una insidia? Insidia es un comentario, alegato dicho o escrito para dañar a otro. Y pese a lo que te parezca, NO es esa mi intención. Sino que no vayas DE CHULO cuando tus conocimientos dejan mucho que desear. Yo soy un ignorante, pero sé cosas, y creo jamás he entrado por aquí de la forma en que tú lo has hecho…
Y si no eres un experto, exprésate de otra forma. Hay millones de formas de hacerlo sin parecer un absoluto prepotente con pies de barro. Porque así has entrado en twitter y aquí. Hay muchas formas de señalar equivocaciones, pero de nuevo, yerras en la forma en la que expresas tus obsesiones. Porque no es la primera vez que entras aquí, aunque antes entrabas con otro/s nick ¿a que sí? Soy un MUY buen detective, créeme. Sé quién eres :P. Simplemente, te pido una vez más, que no vayas queriendo corregir al personal sin saber tú mismo de lo que estás hablando. Eres muy perfeccionista pero no tienes ni idea en ocasiones de lo que dices, porque ciertas matemáticas son sutiles y no pueden aprenderse fácilmente. ¿O es que piensas que todo el mundo sabe lo que es el álgebra universal moderna o la geometría interuniversal que cierta persona dice haber inventado? Queda muy mal eso de no ser experto o físico profesional y querer corregir a algunos que sí lo son, sean más o menos conocidos en el ámbito y el corrillo científico. Pero no sobrevivirías jamás a un escrutinio matemático serio. Y lo digo con pesar, porque yo también tengo mis limitaciones (que conozco), pero tú, al parecer, prefieres DE NUEVO, equivocarte en las formas. Y eso, perdona, pero ya quedó claro que no se puede permitir. No te voy a pedir que sepas lo que es manejar la cohomología de haces, las geometrías de Serre, la teoría de esquemas, o los útiles del análisis fractal y de grupos cuánticos o la geometría espectral de Connes, como sí las conozco yo (no por supuesto al nivel que desearía), pero sí te diré que saber de Física pero también de Matemáticas es algo más que argumentar o especular sobre un conocimiento superficial de diferentes disciplinas. No lo digo para dañarte, ni lo he dicho antes, te lo digo para que te bajes de ese submundo virtual en el que estás metido y que te hace ver errores ajenos (incluso cuando no son «evidentes» para los que sabemos lo que quiere decir quien usa cierto lenguaje), pero te hace decir auténticas barbaridades pensando que comprendes lo que dices o haces. Lo digo sin ofender, porque tú ofendes generalmente cuando te expresas (y no veo que haya cambiado tu actitud: sí te he puesto a prueba ¿y qué? ). Y te digo esto: No con propósito de dañar, sino de que entiendas de una vez de que para saber ciertas cosas, no basta con leerlas, y mascarlas, … El verdadero saber, lleva tiempo. Acumularlo, o simplemente fagocitarlo y divulgarlo o extenderlo no es fácil. La prueba es cuánta gente en el mundo tiene problemas para aprender. Y uno debe saber cuál es su «nivel». Incluso para alguien como yo, que no aprendo lento, entender cualquier cosa me lleva más. Los algoritmos para las matemáticas están bien, inventar nuevas teorías y nuevos objetos no es fácil… Te lo digo con respeto, porque en ocasiones piensas que puedes crear objetos matemáticos «correctos» sin esfuerzo, y no es así. Para nada. La verdadera matemática, la profesional, es mucho, mucho más dura y cruenta.
Un cordial saludo…E insisto, una vez más:
1) Cambia tu estilo de comentar. Hazlo de forma más humilde.
2) Cuida tu lenguage. Se puede ser perfeccionista, pero luego deja que te critiquen, porque te sienta muy mal y lo disimulas muy mal.
3) NO esquives las preguntas con otras preguntas. Y más cuando yo sí te contesto.
4) Deja de autovotarte y de votar negativo a quien te cae mal. Yo no voto negativo a no ver que vea barbaridades de bulto, pero esta vez, y sin que sirva de precedente, no votaré negativo tus comentarios.
5) ¿Debo interpretar que no vas responder a ninguna de mis preguntas de arriba?
Hay un problema secundario, en esto de saber si uno es fisico o matematico, y es el de la bibliografia; estamos hablando por un lado de material de los ochenta y por otro de cosas matematicas; justo las areas en las que el Arxiv cojea y, si no hay suerte con el KEK, hay que pasar por una paywall, de PROLA o de Elsevier, o tener acceso al material fisicamente. No es lo mismo debatir cuando alguien no tiene acceso a material que cuando puede verificar las cosas simplemente bajando a la biblioteca (hay una historia de Hilbert sobre un debate acalorado donde el speaker, sintiendose insultado, abandona la sala… por la puerta de la biblioteca. Lo que causa que Hilbert se quede un cuarto de hora esperandole pensando que ha ido a buscar algun material para argumentar).
Hola amarashiki. Lamentablemente, el debate se ha dirigido por tu parte al ataque personal y asi es dificil continuar. Es cierto que dije que habia ideas equivocadas cuando mantuvimos el debate por twitter: me referia principalmente al texto que escribio Alejandro (y nombre algunos errores), pero veo que te lo has tomado como un ataque personal. Dejame comentar no obstante algunas cosas:
«»Por otro lado no voy a responder a tus inquisitorias preguntas porque no eres quien para examinarme de nada, y no tengo por que saber la respuesta a tus preguntas.(…)” y luego me pides que yo SÍ tengo que responderte a tus preguntas (de las que sé evidentemente las respuestas). Evidementemente, no es un trato muy justo y equitativo. »
Yo te he pedido una explicacion mas profunda y referencias relacionadas con una afirmacion que tu has hecho con el afan de aprender y aclarar lo que se. Tu me haces preguntas para examinar mis conocimientos. La diferencia es obvia, no creo que haga falta resaltarla. Y por cierto, todavia no has aclarado como sale la double field theory de E_{11} en los papers de West, pero no te preocupes, no insisto mas :). Y por supuesto, yo no he votado en negativo a nadie ;). Bueno, veamos si podemos hablar un poco de Fisica (y Matematicas)!:
1) Me referia a que no se han construido y clasificado todos los gaugeos posibles de todas las Supergravedades. Ni siquiera se sabe si todas son embebibles en Teoria de Cuerdas o no.
2) No recuerdo haber hecho ninguna cita «historica». Afirmar que tengo problemas para entender «el lenguaje de las teorias KK» me parece muy bien como opinion personal tuya, asi que poco mas tengo que decir.
3) Tus preguntas no aportan mucho a la discusion, pero las respondo: si se lo que es una variedad algebraica y lo que es un «manifold» y las diferencias y similitudes entre ambas.
4) Tu respuesta aqui carece de sentido, y ademas me llamas mentiroso ;). Pero bueno, en fin, voy a intentar explicarme: cuando se compactifica supergravedad se obtiene tipicamente una supergravedad cuatro dimensional con un potencial escalar. Dicho potencial escalar puede ser negativo definido o positivo definido o no definido. Para que la teoria describa correctamente la cosmologia debe ser positivo definido y tener un minimo estable tal que exista una solucion de vacio de tipo dS (que es lo que se observa experimentalmente). No obstante, las compactificaciones de supergravedad tipicamente producen potenciales definidos negativos y por tanto se obtienen vacios AdS, que son buenos para la dualidad AdS/CFT pero no para describir el universo en el que vivimos. Solucionar este problema para poder incorporar la cosmologia a la Teoria de Cuerdas fue dificil, y se logro en el famoso paper KKLT, donde se logro una compactificacion con un vacio dS suficientemente estable.
Ya que tu has calificado negativamente repetidas veces mi manera de escribir, los conocimientos que tengo, dejame hacer un comentario sobre lo que yo percibo de ti:
No escribes de manera conexa y ordenada. Es obvio que tienes un gran afan por aparentar ser experto en todo, y, no se si esa es la razon, pero acabas escribiendo textos en los que saltas de una cosa a otra, de una teoria o tecnica matematica a otra sin conexion alguna solo para nombrarla e intentar dejar claro que lo conoces, cuando es obvio que solo conoces los detalles superficiales. Dejame ponerte un ejemplo citandote:
«Hay muchas variedades diferenciables que no son algebraicas en absoluto (en el sentido que supongo dices), un ejemplo son las superficies K3 o más generalmente sus generalizaciones en dimensión superior como son las variedades Calabi-Yau.»
Aqui supuestamente hablas de variedades diferenciables que no son algebraicas.
«Precisamente, uno de los problemas del “landscape” es que no hay forma de seleccionar la topología y geometría de la variedad sobre la cual compatificar. Y dado que hay transiciones entre las diferentes posibles geometrías, no podemos seleccionar ninguna. Como sabrás se
habla de que hay hasta 10⁵⁰⁰ posibles Calabi-Yau…»
De repente, y sin venir a cuento, hablas del problema del landscape.
«“Naive” KK se hace en hipertoros, porque es lo más manejable, pues nadie sabe aún no ya calcular las autofunciones sobre ciertos espacios, sino simplemente saber cuántos de ellos existen…»
De repente te pones a hablar de KK en «hipertoros» y autofunciones en «ciertos espacios»
«En parte, todo el enfoque de degravitación basado en espacios que son un retículo está basado en la idea de simplificar el asunto al igual que se hace en lattice QCD con los campos, aunque hay resultados ciertamente interesantes, tampoco ha habido una…»
Y de nuevo de repente, cambias de tema y te pones a hablar de «degravitcaion», «lattice QCD» y a hacer afirmaciones sobre el estado del campo propias de un experto.
Esto que he ejemplificado lo haces continuamente. Y, quiza me equivoque y seas un genio, pero no se puede saber de las miles de cosas que mencionas en tus desconexos saltos en profundidad, y al hablar contigo la conclusion es que hablas de mil cosas pero no dices nada con «chicha» de ninguna, solo comentarios vagos.
Hmm, no nombraste algunos errores, que no digo que no los haya (no era el proposito del post abundar en la precision, sino dar idea de alternativas que normalmente no se contemplan). Te limitaste a repetir una coletilla de que algo era incorrecto, en plan como Gila se paseaba al lado de Jack el Destripador diciendo «alguen ha matado a alguien». Despues, como se produjo el calenton con @amaraski, dejaste de seguir algunos hilos donde no estaba claro que pudieras ganar el debate y saltaste a hacer mas preguntas.
He de decir que yo tambien percibi que tu proposito era agresivo dado que antes de mencionar cualquier posible error arrancaste lanzandome una pregunta trampa, de «examen», la del numero de componentes de un fermion, de la que conocias la respuesta. Al aclarar Francis (y Amaraski) que la supuesta incorreccion que asociabas a esa preguna en realidad solo se debia a un problema de mi redaccion, saltaste de tema. Y si que es cierto, que tal como escribo, en algunos casos, el indeterminado «un» parece que lo confundo con el determinado «el».
Y es acojonante que incluso ahora te quejes de que te pregunten si eres fisico o matematico cuando fuiste tu el que salto la liebre, con una pregunta de ese tipo. Puede que tu recuerdo de la secuencia de eventos no sea ese; el mio es que eres tú el primero que pregunta por credenciales, mediante el circunloquio «¿Habeis calculado completamente…?» Al que yo respondo, @amaraski responde, pero tu olvidas responder.
Lo de olvidarse de unas respuestas y hacer otras preguntas llego a desconcertarme. Durante quince segundos llegue a tener tu test de Turing en suspenso y plantearme si era posible alimentar a Racter con todos los abstracts del arxiv y mandarlo a trollear por twitter. Por otro lado, un buen trolleo muchas veces atrae más publico a un tema, asi que no he llegado a cabrearme ni ofenderme.
Hay que añadir un disclaimer: que tras el primer comentario del tipo Gila, fui yo el que provoco, por DM, a Kac-Moody a que entrara con mas detalle… creo que tenia cierto derecho a ello, como aludido, pero tambien es posible que con ello haya provocado toda esta deriva.
Kac, intentaré ser conexo (aunque creo que es fácil seguirme) ya que tú pareces que no enlazas cosas:
1) Para nada te he atacado personalmente. Simplemente te he puesto a prueba de manera fría. Tú sí que has atacado a la gente por aquí o en twitter con tu lenguage (al menos desde mi sistema de referencia).
2) Sobre mis respuesta. ¿La has leido?¿Te las leido el paper de West? Es simple. El argumento de E_{11} (paper que te cité usando mi memoria, puedes creerlo o no) es que incorporándola a M-theory lleva a la introducción de dos campos (eso lo dice en el abstract del artículo que encontraste). No sé si sue en uno en el que hablama de SL(32)-deja que lo mire en mañana, tengo mi carpeta de papers de West en el armario del salón- o en otro posterior de 2004. Argumento: E_{11} symmetry (cierta álgebra de Kac-Moody, jajaja) permite cambiar las variables dinámicas en M-theory de forma que el campo gravitacional se codifica en dos campos. Esto llevó (no recuerdo si en ese paper o en otro posterior) a la idea de incorporar la dualidad T a nivel dinámico (y no sólo en la worldsheet) como simetría de la teoría. Puesto que la dualidad cambia espacios y tiempos «grandes» es natural introducir una teoría gauge en la que X y 1/X sean variables diferenciadas. Si tienes 4 X, tendrás 4 1/X, en general, si tienes D X, tendras D 1/X. Ésa es (puedo equivocarme ¿eh?) la historia del origen de double field theory. Como entenderás, hasta que la gente le interesó, pasó un tiempo, … Hull y Zwiebach entre 2006-2009 fueron los que introdujeron esta terminología (double field theory), aunque ya había sido empleada antes en otros contextos, en teoría de sugra y superstrings. Sin embargo, la idea puede también entederse desde la two-time physics de Bars, o la propia dualidad electrognética (que es similar en concepto a esto, pero con campos y no con coordenadas de espaciotiempo).
3) Sobre los gaugeos de toda supergravedad. ¿Eres experto en el tema? Y no me vale que me digas que no. ¿Qué quieres decir con gaugeos? ¿Transformaciones gauge? Evidentemente cualquier teoría que quiera ir más allá de SUGRA maximal y quiera definir M-theory tendrá que enfrentarse a la cuestión de qué tipo de simetrías y gauge transformacions (sean YM o generalizadas o de cualquier otro tipo de gauge). Eso es obvio. Si te refieres a la clasificación de las cargas y campos gauge, evidentemente el problema es clasificar los campos gauge que viven en las teorías. El approach de West, el de double field theory y otros que usan geometrías excepcionales y/o métodos de teorías de supertwistores y superespacos tensoriales extendidos pretenden encontrar la forma de hacerlo. De hecho, si lees los artículos de Paul, te encontrarás que es muy fácil tabular las dualidades usando esas álgebras de Kac-Moody especiales definidas por E(11).
5) Me citas (gracias) y señalas que no viene a cuento para nada el problema del landscape y las compactificaciones en Calabi-Yau. ¿En serio dices que no tiene nada que ver? ¡Si es el problema que les ha dado de cabeza a todos en string theory! Es por eso (y otras cosas que no no te voy a comentar para ser bueno) por lo que sé que eres tú y no yo quien no sabe lo que dice. Para definir una teoría de supercuerdas a nivel cuándo, incluso cuando compactificas, hace falta definir un «vacío». Lo que se esperaba tras lo de Green y Schwarz (y la felicidad de Witten en los 80) era que la clasificación de las variedades de Calabi-Yau ayudara a seleccionar el vacío. El problema fue ¡todo lo contrario! Hay demasiadas Calabi-Yau en 6 dimensiones sobre las que compactificar (y eso sin conocerlas todas y sin haber solucionado el problema de cuantas son cuánticamente equivalentes por medio de transiciones), y eso produce un ingente número de «falsos vacíos» cada uno reproduciendo los parámetros del modelo estándar (ajustar los acoplos es «doable», como las masas), la cuenta no es mía…Por lo tanto, ahí no diré que he hecho las cuentas yo (como sí en otros casos, como calcular cierta integral de cuerdas a dos loops, pero es otra historia). Sin embaro sé que la cuenta sale de contar Calabi-Yaus «independientes» y por la cuestión del número de «cargas» generalizadas y sus respectivos flujos producidas por su particular geometría (no he repasado desde hace algún tiempo geometría compleja, pero creo que el punto era por los ciclos y cociclos de homología, esto es, por la (co)homología de los operadores $latex delta, bar{delta}$ de dichas variedades, pero puede haber cierta imprecisión aquí, no recuerdo los detalles de esto porque nunca me interesó porque siempre lo vi MUY artificial. Y relacionado también, aunque veo que no le pillaste el punto, cuando compactificas sobre el círculo, el espectro sale por las autofunciones del laplaciano en 5D=4+autofunciones del circulo). En variedades Calabi-Yau, el espectro sale por las ecuaciones y autofunciones del espacio sobre esas variedades (como ocurre con el círculo en el caso KK normal). El problema, insisto, es que no podemos enumerar los Calabi-Yau o saber cuántos son equivalentes. Las autofunciones sobre esos espacios están relacionados con la geometría complea de los operadores que te he citado, justo como en el espacio usual está relacionado con $latex star dstar psi=Delta psi$ en 5D=4D+1D (círculo). No comprendemos suficientemente los «vacíos» o espectros que dan las Calabi-Yau. Como ves, no era ni inconexo ni difícil de entender…Para hacerte comprender el problema de la enumeración de los vacíos mencioné degravitación y las teorías gauge en el retículo (que se usan hoy día con superordenadores para entender confinamiento y el espectro de QCD, por ejemplo, entre otras cosas). No era inconexo. Simplemente, quería destacarte que en una teoría no contínua (si sabes algo de lattice gauge theory), puedes simplificar mucho el asunto de las compactificaciones o cambiar el tipo de espectro normal de KK por algo más similar a lo que te encuentras en, verbigracia, la teoría del estado sólido. El parámetro de lattice y el «número de puntos» en los que discretizas la red y donde colocas los campos de materia (fermiones), te permite computacionalmente hablando tener siempre una teoría bien definida y finita, controlable (al menos si no introduces interacciones demasiado complicadas y exóticas, pero como sabes, el modelo estándar es una simple teoría $latex gphi^3+lambda phi^4$, el resto de interacciones están «prohibidas» por simetría. Análogamente, y con esto termino este punto, una teoría con dimensiones extra consistentes en una lattice o un número finito de puntos es mucho más manejable que todas esas Calabi-Yau en el landscape. Simplemente, era notarte ese punto. Pero ya veo que no lo entendiste. Una pena.
¿Afirmaciones de experto? No diré que lo soy porque mentiría. Pero da la casualidad de que YO cursé TODAS las asignaturas del Máster sin estar obligado a ello (y porque no me dejaron pasar los créditos cogiéndome una asignatura no docente). En Lattice QCD aprendí algunas cosas, no como para hacerme experto porque yo no sé apenas nada de computación, pero comprendo bien lattice QCD desde el máster, porque resulta que F.J.Ynduráin (sí, el mismo que dices no tenía ni idea de cuerdas sin TÚ haberle conocido como sí lo conocí yo en persona) era experto en QCD y aunque él me dió análisis complejo, yo aprovechaba para preguntarle un sin fin (casi) de otras cosas de física y su especialidad, la QCD (tiene dos conocidos libros de QCD) y algo menos lattice (aunque sus libros en español no me gustan, debo reconocer que la introducción que hace a teorías gauge en el retículo en sus libros de mecánica cuántica es la mejor introdución posible en lengua española hasta la fecha).
Finalmente, no pretenderás que un blog como el de Francis me ponga a escribir cosas excesivamente técnicas (aunque ciertamente me he concedido licencias de vez en cuando, supongo Francis sabe lo que digo y otros lectores). Para eso tengo mi blog. Aquí, y muy a mi pesar, intento limitarme y no me es fácil. Porque me aburro con extrema facilidad, y supongo que debido a que ya no soy un adolescente, ya no soporto igual de bien (pese a que mi paciencia es grande, aunque no te lo creas), cierto tipo de comentarios. Si te da la impresión de que voy en saltos, posiblemente sea porque tú no conectas lo que yo sí, y porque posiblemente no quiero meterme en cosas demasiado técnicas que me llevarían a introducir matemáticas sofisticadas (que introduciré en mi blog, está en mi road map, tranquilo por eso). Además, yo pienso (no sé si acertadamente o no) no como Hawking y otros que prefieren evitar en libros, o blogs o charlas todo aparejo matemático, incluso el más básico. Cierto es que siendo pragmáticos, las ideas en física o incluso matemáticas pueden expresarse con palabras (ciertamente así es). Pero el lenguaje usual (tanto hablado o escrito) es sumamemente impreciso para explicar ciertas ideas que las matemáticas y el rigor lógico y la razón sí hacen.
Si quieres chicha, sigue mi blog a partir de septiembre, o léete bien las referencias que en ocasiones tú mismo has citado, porque dudo mucho que las entiendas. Y si lo haces, deberías escribir sobre ellas. Pero te diré algo, las geometrías excepcionales llevan con nosotros mucho tiempo (palabra clave: cuadrado mágico). Como otras tantas ideas, se mejoran y reinventan (piensa en las teorías KK) cuando se acumula masa crítica para una «revolución» y se produce el siguiente salto de conocimiento (teoría de las revoluciones científicas ¿tengo que citarte al filósofo de este tipo de teoría del conocimiento?). Tus comentarios y extrema habilidad para evitar mis respuestas y escurrir el bulto de delata. Pero vamos, tú sabrás. Lo que más me entristece, es ver que no has aprendido nada a nivel de actitud. Mira que seguir empeñado en aplicarme la psicología inversa para que sea yo y no tú el que demuestra conocimiento nominal y no superficial sobre el estado de la Física y Matemática contemporánea es ciertamente bastante ridículo. Habrías podido tener éxito años atrás, cuando yo era débil en inteligencia emocional o psicología. No ahora, pero en fin. Tú sabrás por qué lo haces, pero no dice nada bueno de ti eso. Para aprender, hay que reconocer la ignorancia. Yo lo hago. ¿Tú? Lo único que has hecho es intentar retorcer mis palabras para que mis argumentos parezcan bizarros o hasta banales. Cuando creo, y pienso, que tiene plena consistencia (no como los tuyos, en general, pues algo con sentido has dicho arriba).
En relación a todo esto…No se trata de una competición, cuando uno habla con alguien de algo, uno debe saber a qué nivel puede mantener la charla. Es difícil y más para mí aquí y más en mi blog (no te imaginas mis problemas en la vida diaria con esto pese a que ahora he mejorado un poco). Por eso, lamento que hayas visto insidias y que quiero aparentar ser un experto en todo. No lo soy. Pero te diré algo. No tengo muchos amigos. Pero quienes me conocen, todos, incluso los alumnos o compañeros de mí, yo sé lo que decían y dicen de mí a mis espaldas. Jamás diré de mí se un genio porque pienso que no tendría los problemas que tengo ahora mismo si lo fuera (aunque hay gente que me dice que dicho razonamiento parte de un supuesto falso) ni lo que han dicho de mí. Pero sí tengo mi autoestima, mi autoconcepto y creo que sé hasta dónde llegan mis conocimientos. Si lees hasta aquí con cuidado, habrás detectado que al menos en dos momentos, reconozco hasta dónde sé (y lo que no sé). El problema lo tienes tú y no yo, no ya porque me hayas llamado insidioso y experto de todo (no lo soy de casi nada, pese a que toda mi vida la he dedicado a reducir mi ignorancia), sino porque hablas de segundas personas sin haberlas conocido o siquiera chateado o mensajeado con ellas (Ynduráin, Alejandro o el propio Francis). Aunque veo que en algunas cosas has cambiado de táctica, en otras sigue siendo lamentablemente el mismo (también es cierto que para cambiar la forma de ser una persona requiere tiempo, pero lo has tenido) tipo arrogante. No digo que cambies de repente, pero al menos inténtalo, ganaremos todos. No dudo que yo mismo parezco pedante (no quiero ser Lubos Motl, me da miedo eso que me dijo Francis hace casi ¿un años ya?el tiempo vuela), pero yo intento mejorar. Tú sigues igual hasta donde yo puedo observar.
En fin, nada más. Tengo aún que leer un par de cosas antes de acostarme. Que es tarde y mañana quiero avanzar en otro par de cosas de preparación de mi site y de los apuntes para clases (versión supervivencia 2.0). Un saludo y espero haberte parecido ordenado, coherente y reflexivo (quizás …Insightful or enlightened?) esta vez.
Respondo primero a Alejandro:
El texto que escribiste contiene errores e imprecisiones diversas. Por twitter comente alguna pero el formato de los 140 caracteres no permitia una discusion completa del tema asi que lo deje pasar. Obviamente a estas alturas ya no me merece la pena debatir dicho texto.
Ahora le toca a amarashiki:
Voy a omitir toda alusion personal. La manera en la que hablas de ti mismo en tus respuestas ya es suficientemente ilustrativa.
1) OK
2) No encuentro sentido a la explicacion que das. En el paper de West no se da ninguna relacion entre E_{11} y la double field theory. Si es asi por favor indicame la pagina.
3) No soy experto en el tema. Gaugear una Supergravedad es escoger de manera consistente un subgrupo de isometrias de la variedad escalar embebido en el correspondiente grupo de U dualidad y hacer que la teoria sea invariante bajo transformaciones locales de dicho subgrupo manteniendo, por supuesto, la supersimetria. Por cierto, que es un «superespacio tensorial extendido»? Y que conste que te lo pregunto porque tu lo nombras.
5) Lo que no viene a cuento es que teniendo que responder a algo concreto, derives en todas esas diferentes cosas, que comentas superficialmente, enmascarando la respuesta a lo que se te pregunta, respuesta que finalmente nunca das.
El comentario respecto a F.J.Ynduráin era sencillo: si esta persona dice que la Teoria de Cuerdas es ciencia ficcion (que es la motivacion de mi comentario) entonces esta persona no sabe de Teoria de Cuerdas.
Veo que para ti el tener titulos y haber cursado una carrera o un master es muy importante, tienes cierta «titulitis». Casi parece que intentas utilizar el argumento de autoridad. Sin embargo, este debate ilustra perfectamente que un titulo no implica hablar con conocimiento de causa.
Voy a ir por las buenas, a ver si de una vez entiendes (veo que no):
1) Sin comentarios. Aunque es realmente enfermizo que me digas antes de 1 la siguiente perla que se contradice en dos frases: «(…)Voy a omitir toda alusion personal. La manera en la que hablas de ti mismo en tus respuestas ya es suficientemente ilustrativa.(…)»
2) ¿Me has leido? Te he dicho arriba que en el paper de 2001 West simplemente codifica en 2 campos el campo gravitacional en M-theory. Te dije arriba que creo la hipótesis de «double field theory», o sea doblar los campos por el argumento que te he dado, fue posterior. 2003 ó 2004. Ahora no te lo puedo mirar, estoy corriendo para cambiar la dirección de las imágenes de mi blog y preparando apuntes para las clases que espero dar a partir de septiembre para sobrevivir. Cuando termine, espero antes de fin de agosto puedo serte más específico y buscarte el paper concreto. Pero no busques por double field theory, porque como te he dicho arriba, la terminología es de Hull y Zwiebach (no recuerdo si la introdujeron en un paper y charla en 2006 ó 2007, pero es de esa época). Lo que he intentado explicarte, es que para llevar la simetría T al espacio-tiempo como simetría local, se tienen que doblar las coordenadas. Esto es «natural» en el sentido siguiente: las coordenadas en string theory se pueden interpretar como campos conformes sobre la world-sheet, así que es ciertamente intuitivo asimilar la dualidad a una simetría O(D,D). No busques en los papers de West las palabras explícitas porque no lo hace, pero sí, a partir de E(11) comenta la necesidad de doblar los campos, en paralelismo a lo que hace en 2001 con el campo gravitacional, para tener coordenadas/campos de forma más simétrica. El paper donde hace el comentario concreto, está en 2003 ó 2004. Lo recuerdo porque estaba la acabando la carrera (con más pena que gloria) por aquella época.
3) Pues para no ser experto, te concedes licencias para definir palabras y conceptos que son cuando menos, sospechosos. ¿Supesespacions tensoriales extendidos? Para fardar cómo lo haces de sugra, es cuando menos notable que no sepas el trabajo que hizo el actual presidente de la RSEF.
4) (me comí el punto 4, es lo que tiene escribir por la noche a las 4 de la mañana, así como escribir incorrectamente el laplaciano o más generalmente el operador de onda en términos de formas diferenciales, mea culpa) ¿Qué respuesta no te he dado TARADO mental? Te he respondido a lo de West, te he respondido a las referencias (te he acotado la búsqueda). Te he respondido a lo del landscape (que por supuesto ahora evitas y te pones a decir que no respondo, ¡toma!). Hasta te he dicho sibilinamente lo que es E(11), mientras que tú has esquivado TODAS mis cuestiones técnicas.
5) Sobre Ynduráin, te dije que Ynduráin pensabe que string theory era ficción ciencia (no ciencia ficción). Por supuesto, la realidad podría demostrarnos que es verdad o mentira. Era su opinión, y puedo decirte que el tipo sabía de cuerdas (no en vano él era experto en S-matrix, variable compleja -escuela rusa-, y conocía la teoría bastante bien porque había conocido el modelo de Veneziano y sus ramificaciones en los 70). Tú simplemente no puedes sojuzgar a alguien que no entiende (o más precisamente no entendía, porque murió de cáncer hace algunos años) sin haberle conocido en su despacho, ¿no crees? Una cosas es ser un fan y adepto de string theory, un follower, y otra es conocer la teoría pero ser muy crítico, como Ynduráin o el mismísimo Feynman. ¿También vas a decir que Feynman no la entendía?
6) Si yo estuviera obsesionado en tener títulos por el papelito, ya me habría acercado a algunas personas para hacer la Ph.D, siendo un pelota (pero no me gusta eso y quiero ser «libre»). Pero haber estudiado una carrera y un máster, digo yo, me otorga al menos ciertas facultades (que por cierto ya tenía en mi época premáster pero que debido a mis depresiones no salían). Para mí no es necesario que tengas un título para discutir contigo, pero al menos respeta lo que el poseer dichos títulos (no el papel, que es nominal) otorga. ¿O tú te operarías con un doctor sin títulos?¿Irías a un dentista que no tiene acreditación oficial? ¿En serio piensas que los títulos más allá del papel y del dinero que cuestan, en general, no indican algo? Ojo, que yo conozco a gente que estudia Ph.D o es post-doc y no me comprende y no entiende muchas cosas que soy capaz de hacer o discutir, pero eso es otro asunto. Los títulos no otorgan categoría, pero sí son un mínimo para determinar la capacidad para ejercer ciertas funciones. Digo yo. Poseer un título claro no sirve para medir tu nivel de conocimiento ni tu autoridad, pero desde luego te da credenciales y «capacadidad de…». ¿O tambiénme vas a decir que el carnet de conducir no sirve para nada?
Finalmente, tu definición de gaugear supergravedad es simplemente absurda: «(…)Gaugear una Supergravedad es escoger de manera consistente un subgrupo de isometrias de la variedad escalar embebido en el correspondiente grupo de U dualidad y hacer que la teoria sea invariante bajo transformaciones locales de dicho subgrupo manteniendo, por supuesto, la supersimetria. (…)». Si no eres experto, deja de equivocar al personal sobre términos que no entiendes y que por supuesto estás lejos de poder calcular…
Dejame empezar por el final, despues te respondo el resto. Dices:
«Finalmente, tu definición de gaugear supergravedad es simplemente absurda: “(…)Gaugear una Supergravedad es escoger de manera consistente un subgrupo de isometrias de la variedad escalar embebido en el correspondiente grupo de U dualidad y hacer que la teoria sea invariante bajo transformaciones locales de dicho subgrupo manteniendo, por supuesto, la supersimetria. (…)”. Si no eres experto, deja de equivocar al personal sobre términos que no entiendes y que por supuesto estás lejos de poder calcular…»
La definicion, obviamente, no es mia. Punto 3) de la pagina dos de http://arxiv.org/pdf/hep-th/9605032v1.pdf o para mas detalles la seccion 6 de dicho paper. Esto es dar una referencia, y no lo que tu haces. Y el que no sea experto en el tema no quiere decir que no pueda opinar sobre el de forma razonada y argumentada. Si solo pudieramos hablar de los temas en los que somos expertos no podriamos hablar de nada.
Er, bueno, eso no es hacer una referencia, ahora estas haciendo una referencia. Antes has extraido contenido de un paper bastante lateral -que un no experto en el tema no lee habitualmente, asi que me intriga si lo has buscado justo para la discusion o si lo tenias ya localizado de antes- y lo has presentado como una respuesta general. Asi que no, no has hecho una referencia. Has hecho una -otra- trampa de debate, que va a ir forzando a cualquiera que se meta en estas threads a tener que ir mirando con pies de plomo y detector de metales donde esta la siguiente mina.
Una referencia casual habria sido al mencionar el gaugeo decir algo asi como «segun practica el equipo de Auria y Fré», o algo asi.
Tu respuesta es «surrealista». Aun asi voy a contestarte, sin que sirva de precedente: no he «hecho una referencia», he dado una referencia donde sale la definicion de gaugeo de Supergravedad que he usado yo y que segun amarashiki es absurda. Dar una referencia es decir el paper concreto y si puede ser la hoja del paper donde figura aquello a lo que te refieres, como he hecho yo. Parece mentira que tenga que explicar esto.
Y respondiendo a tu pregunta: ese paper lo conocia de antes, ha sido imprescindible en mi trabajo de los ultimos meses.
Bueno, exacto, dar referencias es lo que estoy haciendo yo, que o bien doy la linea explicita o bien doy una referencia casual que permite localizarla en un golpe de spires o similar. Por cierto, mas arriba te he puesto la de Castellani donde dice que la tabla 6 dichosa es la tabla completa de variedades posibles en dimension siete, y no «solo las descubiertas en aquella epoca», como parecias pensar.
Sigo:
1) Sin comentarios.
2) Le sigo sin ver sentido a la explicacion. Por favor indicame la referencia, y si esta es muy larga la pagina (como he hecho yo), donde se relacione E_{11} con DFT.
3) Parece que ya no recuerdas ni lo que escribes. Tu has dicho:
» El approach de West, el de double field theory y otros que usan geometrías excepcionales y/o métodos de teorías de supertwistores y superespacos tensoriales extendidos pretenden encontrar la forma de hacerlo. »
Y por eso te pregunto, que es un superespacio tensorial extendido? Tu mismo has usado el concepto, yo no me he inventado nada. No se lo que es y por eso te pido una explicacion, que por supuesto, no das.
4) Insultarme de esa forma (llamandome TARADO mental) te desacredita completamente, y ademas esta muy feo; es de muy mala educacion. No has respondido a ninguna de las preguntas que te he hecho sobre lo que tu has escrito. Como ya te dije, yo no voy a responder a las preguntas que me haces tu salidas de la nada y cuyo objetivo es intentar demostrar que no se de algo. Responder a tus dudas sobre lo que escribo por supuesto si.
5) Sin comentarios.
6) «Ojo, que yo conozco a gente que estudia Ph.D o es post-doc y no me comprende y no entiende muchas cosas que soy capaz de hacer o discutir, pero eso es otro asunto.»
Y sera por que son ellos los que no saben, y no porque tu estes completamente equivocado… verdad?
Alejandro, no te has enterado de lo que dice el paper que tu mismo citas. Has dicho
» Por cierto, mas arriba te he puesto la de Castellani donde dice que la tabla 6 dichosa es la tabla completa de variedades posibles en dimension siete, y no “solo las descubiertas en aquella epoca”, como parecias pensar.»
Lo que dicen en «Castellani, Romans y Warner, NucPhysB 241 » es que dan la lista de todas las variedades compactas M_{7} homogeneas y con metrica Einstein que compactifican Supergravedad en 11 dimensiones a AdS_{4}xM_{7}. Por supuesto, esta no es una lista de todas las variedades en las que se puede compactificar la Supergravedad d=11, ya que no tienen por que ser homogeneas o Einstein o dar lugar a AdS en 4 dimensiones. Asi que hay una infinidad de variedades compactas que no salen ahi y en las que se puede compactificar d=11 Sugra. Por ejemplo, ahi no salen las variedades Sasaki-Einstein, donde si se puede compactificar d=11 Sugra.
Hmm, planteate dos hipotesis: que no entienda los papers o que no te entienda a ti. Por lo que veo, los desencuentros principales son gramaticales: que si un fermion en 11D o el fermion en 11D, que si todas las posibles o todas las de un tipo dado… No se, igual repaso mas adelante en mi blog todos estos lios lingüisticos a ver si son cosa más mia que tuya.
El resto del comentario arriba, donde esta la referencia a Castellani, deberia permitir a cualquiera deducir que no creo que la compactificacion que buscamos sea exactamente una de la lista; creo que al menos debe ocurrir un cocientado por conjugacion compleja que lleve a una compactificacion que aun desconocemos. AdS con homogeneos tenia un papel fundamental, y era su compatibilidad con Freund-Robin, pero en general la lista es importante primero porque aclaraba lo que entiendo por Kaluza Klein (que los campos gauge observados en la naturaleza salgan de la gravedad, como ocurria en el caso original) y segundo porque indica unas condiciones mu simples con las cuales la simetria del modelo estandar es una entre muy poquitos candidatos.
Por orden de simplicidad, diria que primero tenemos S7, con el maximo de simetria posible y asociada al grupo SO(8). Luego las twistted spheres, que aprovechan la peculiaridad de la fibracion de Hoft de S7 para obtener SO(5)xSO(4), esto es la simetria de la base S4 y la simetria de la fibra S3. Fue bastante ingenioso en su dia, y el review de Duff cojea hacia ellas porque es descubrimiento de esos autores. Y luego tenemos los que encontro Witten, con las simetrias del modelo estandar, que parecen ser fibrados de base CP2 y fibra S3. Digo parece, porque no es la forma habitual de construirlos, se suele hacer o bien con una fibra S1 sobre CP2xCP1 o bien por el proceso de cociente desde S5xS3. En cualquier caso, la pista principal sobre la relacion entre la simetria mas amplia posible, la de la esfera, y la que aparece en el modelo estandar, es este cociente del teorema de Arnold-Kuiper-Moser.
No puedes hacer conjugacion compleja en M_{7} porque M_{7} no es una variedad compleja. Que significa «AdS con homogeneos tenia un papel fundamental, y era su compatibilidad con Freund-Robin»?
Me alegra la pregunta porque me da la oportunidad para poner otro par de referencias básicas. El articulo de Freund y Rubin, http://inspirehep.net/record/154579?ln=en, aparece en 1980 y deja claro que 11 se puede compactificar espontaneamente en 4+7 o en 7+4 gracias al tensor antisimetrico de orden 3. De aqui viene toda la industria que hace cosas bien en AdS7 mas cuatro dimensiones compactas, bien en AdS3 mas siete dimensiones compactas. Duff suele referirse a esto solamente con la esfera, por ejemplo en la introduccion a su recopilacion de articulos sobre 11d te dice: «The mechanism of spontaneous compactification appropriate to the AdS4 x S7 solution of eleven-dimensional supergravity was provided by the Freund Rubin mechanism»; pero incluye a todos los espacios homogeneos de la clasificación, o al menos eso me parece. En principio Freund-Rubin es general pero si no fuera gracias a sugra, el tensor antisimetrico seria ad-hoc.
Relacionado, hay un non-go para dimension 10: «Ten into four won’t go», http://dx.doi.org/10.1016/0370-2693(83)91558-7
En cuanto a lo de la conjugacion compleja, fijate que donde necesitamos que funcione no es en S7 sino en la base del fibrado de Hoft, en S4, para relacionarlo con CP2. Lamentablemente, no tengo ninguna familiaridad con la operacion de «branched covering», que parece que es la operacion implicada por el teorema de A-K-M.
A ver Kac (aunque puedes entrar con cualquier de tus otras identidades virtuales, porque sé quién eres):
1) Si decir que no vas a entrar a las alusiones personales pero a continuación añadir que mis comentarios son ilustrativos suficientemente tras un punto y seguido dices que no merece comentarios, engañas como haces siempre.
2) Te dicho que tengas paciencia, porque pese a lo que parezca, tengo otras prioridades ahora. He tirado de memoria para decirte gran parte de las cosas que te he dicho, y de background, pero si quieres el lugar concreto, te pido que esperes unos días. Simplemente, y pese a que estoy de multitasking ahora, no voy a abrir la carpeta de west ahora. E insisto, si mi explicación no te convence, y lees el paper de West pero no te enteras, es TU problema, no el mío. Aún así, prometo darte la frase de West, más precisa que la tuya respesto de la definición de «gauging de sugra», que si lees lo que dices en el paper que citas, …Sinceramente, no es que no sea absurdo, es mezclar churris con meninas. «Gauging» es el proceso general por el que se implementa una simetría gauge en una teoría. Obviamente el punto 3 hace alusiones a lo que comentas, y la sección 6 habla precisamente del «gauging» de SUGRA, pero no es ni con mucho lo que dices, porque ¿sabías que el grupo Sp(2n,R) de dualidad electromagnética NO es el grupo de dualidad U en una teoría de SUGRA? YERRAS por enésima vez, demostrando que no tienes ni pajorera idea de los que es la dualidad U en SUGRA. Por cierto, implementar la simetría gauge en una teoría se presta a otras «definiciones», como por ejemplo definir los estados «modulo transformaciones de gauge», pero claro, tú simplemente citas algo que se parece mucho en vez de tú mismo dar la definición o en qué sentido la haces. Por eso decía que era absurda y lo sigue siendo tu definición. Por supuesto, podemos acordar que «gauging» es la elección de grupo gauge Y/O encontrar el espacio formado por el conjunto de configuraciones de campo modulo transformaciones de gauge. Pero de nuevo, te equivocas.
3) Perdona, pero sí recuerdo lo que escribo. Otra cosa es que me dé la gana por contestarte o no, porque tú no has respondido a las mías ¿verdad? Yo sí a todas salvo al lugar concreto donde West propone duplicar los campos. Te digo que es un paper suyo de 2003 ó 2004 (pero ya veo que eso te da absolutamente igual). Te he dicho que double field theory es una terminología posterior (te da igual). Te he dado la explicación intuitiva del origen de la O(D,D) symmetry ( y sorprendéntemente ni te convence mi argumento, ¿quizás porque no lo has visto en ningún paper o libro para plagiarlo como has hecho con el artículo de 2006?, y te sigue dando igual). En fin. No te preocupes, que te encuentro la frase de West en cuanto acabe con este aburrido renombrado de imágenes y pasada de apuntes (es que no quiero estar el curso que viene bailando con papeles o libros, me estoy cocinando mis propios apuntes para Bachilerato y universidad-espero tener suerte y pillar una academia de asignaturas universitarias si no me sale de una vez la Ph.D que quiero desde hace un par de años). Sé un poco paciente. Sobre lo del superespacio tensorial extendido, ¿tengo que decirte lo que es cuando tú te has negado sistemáticamente a darme respuestas? Hombre, de nuevo tienes una curiosa percepción sobre lo que es una discusión en igualdad de condiciones. Aunque te he dado la pista. Otra cosa es que no sepas quién es el presidente de la RSEF.
4) Mis preguntas no están salidas de la nada. Me explico, porque a tu cabeza parece que le sigue faltando capacidad para hacer conexiones lógicas y seguir una conversación evidente:
i) Te pregunté si eras físico porque para alguien que no lo es, te concedes muchas licencias. Curiosamente, a mí, que sí que lo soy, sí que me las quitas por ¿no tener una Ph.D? De nuevo vuelves a contradecirte. Creo que tienes evidemente una forma muy diferente de tratar a las personas según se aplique a ti o a los demás la posesión de lo que tú has llamado «titulitis».
ii) Te pregunté lo de las «citas» de «KK» porque para hablar de geometrías excepcionales o decir algunas de las burradas que has dicho en twitter, hay que desconocer bastante la historia de la Física moderna. Me explico (espero): ante la discusión sobre el por qué se abandonó el enfoque tradicional de KK, tú simplemente haces ciertamente algunos malabarismos textuales, como si efectivamente hubieras calculado las cosas. Respecto a lo de Calabi-Yau o el landscape, te equivocas y evidentemente pasas de ello luego para no quedar en mal lugar. Sobre los hipertoros me criticas, cuando evidentemente, cualquiera que haya estudiado física teórica entiende por qué KK y el mecanismo de Scherk-Schwarz no se han abandonado. Pero vamos. tú mismo.
iii) Enésimo error. Mencionas que al reducir supergravedad, se obtienen potenciales escalares que producen generalmente máximos/mínimos cuando se minimiza el potencial (estoy siendo algo burdo, perdona, pero es para que nos entiendan). Es simplemente mentira como decías que produzca siempre un AdS. Eres tú, creo, quien ¿no recuerdas lo que has dicho tú mismo arriba? Te lo recuerdo. En tu segundo comentario de este artículo, después del de Laura, y tras tu punto 7) dices nada menos lo siguiente:
«(…)la compactificacion de N=1, D=11 a 4 dimensiones en general produce un potencial escalar, y el minimo de dicho potencial puede ajustarse casi como se quiera siempre y cuando de lugar a un vacio AdS. (…)»
Eso no es verdad, hay formas de reducir SUGRA que NO son para nada vacíos AdS. El hecho de que se haga con AdS es debido, permite que insista a algo que YA TE DICHO y que ignoras en tus respuestas, a la correspondencia AdS/CFT. Además, la reducción dimensional que comentas, en términos técnicos, produce un (hyper)Kähler (super)potential que efectivamente tiene mínimos. Pero el punto es que nada permite seleccionar cierto (super)potencial que otro, la reducción dimensional como supongo sabrás se carga supersimetrías (así como la elección de condiciones de contorno para los campos bosónicos o fermiónicos), y el hecho de escoger unos sobre otros es totalmente «model dependent». Uno de mis profesores del Máster, en una cena de grupo, dijo que el campo de la supergravedad en término de gravedad cuántica efectiva, se ha vuelto un problema esencialmente de determinar o seleccionar cierto potencial Kähler sobre otros ( y no es un cualquiera). Para nada el ajuste es «como se quiera siempre que sea un AdS». Eso o bien te lo has inventado tú mismo o bien espero cites una referencia en la que se diga tal correspondencia (en el artículo que has citado arriba no se dice eso para nada). Además, te digo más…Lo de encontrar un vacío dS en SUGRA «estable» sigue siendo un problema no resuelto importante. El paper que mencionas en el que según tú dices que se soluciona el problema haciendo que el vacío dS sea «suficientemente estable» no hace tal cosa. Y es hoy día aún poco entendido el asunto de la dualidad gauge/gravity en dS como lo es con la conjetura de Maldacena AdS/CFT. Ciertamente es similar, pero hay diferencias notables entre un AdS y un dS a nivel cuántico. Es decir, aunque algunos grupos han investigado el tema, hay problemas sutiles en la correspondencia dS/CFT que no están entendidos (en particular la establidad, pero también el tema de la correspondencia entre operadores en la teoría conforme con las soluciones de supergravedad con constante cosmológica positiva).
En resumen, ni la correspondencia del los mínimos del potencial con el AdS es «1-to-1» ni estamos forzados más que por tener un medio para calcular las cosas. Es un comentario totalmente model dependent con muchos prejuicios.
Por cierto…Un inciso…El paper al que te refieres KKLT en el que según tú se soluciona el problema del vacío dS no soluciona los problemas de fondo. Es una propuesta (no sin problemas que se han comentado por diversos grupos de supergravedad y algunos foros). El problema del vacío de dS es sutil, porque si no, ya se habría lanzado todo el mundo a hacer QFT en dS spacetime (que aparentemente es en el que vivimos) en vez de hacer teoría cuántica de campos en Minkovski (flat!) spacetime. El problema con dS QFT es que es teoría cuántica de campos en espaciotiempo curvo, y eso, a nivel cuántico, ¿sabes la cantidad de problemas que da? De nuevo, permíteme que te diga que es un grueso error el tuyo al citar un paper (del que por cierto no das el código del arxiv, sino las letras de sus iniciales). Para que los lectores se aclaren de qué paper citas aquí asumiendo que todos lo conocen:
arXiv:hep-th/0301240 de Sitter Vacua in String Theory
Shamit Kachru, Renata Kallosh, Andrei Linde, Sandip P. Trivedi
Como ves, yo sí soy capaz en pocos segundos de identificar de donde sacas tus copy-paste para aparentar saber de lo que hablas para llegar a tus fuentes (y tú no eres ni capaz de encontrar las mías encima de que te he acotado la búsqueda más que tú la tuya). Dicha construcción es KKLT una MUY particular. Es cierto que como dices que es «difícil» lograr vacíos tipo dS como el que nuestro universo es, pero es lo único correcto que dices, porque este paper no soluciona para nada la cuestión de la estabilidad (el vacío es metaestable, ciertamente muy estable). De hecho, complica las cosas. Pero vamos, tú puedes seguir jugando a que entiendes lo que dicen ahí, porque ciertamente no lo tienes muy claro. Nota: yo conozco este paper desde hace tiempo, porque una de las áreas en las que he hecho cálculos, son con los espacios de De Sitter. Te diré, además, que los propios expertos de teorías de cuerdas no lo ven para nada como una solución. Además, que como se comenta ahí, los moduli no seleccionan para nada el dS, lo seleccionamos nosotros (y te aseguro que NO sin esfuerzo y NO sin problemas). Tú has aludido a este paper como una especie de panacea, pero no lo es para nada. Vale, es un paper de Linde, Kallosh , Kachru y otro que conozco menos, pero eso no quita de en medio los problemas. Es posible que sea una solución, pero es muy forzada y a saber si es compatible con el Universo observado. Además, como pueden leer nuestros lectores, del propio abstract, los autores comentan que son ellos quienes «ajustan» los moduli: «(…)one can make models with all moduli fixed, yielding a supersymmetric AdS vacuum. (…)» Te has vuelto a columpiar…Lo siento. Fue un buen intento. Pero no cuela. Al menos, no conmigo.
Finalmente dos cosas adicioneales:
A) De nuevo insistes en hacer juicios que yo no he hecho para nada. Tú dices: «(…)Y sera por que son ellos los que no saben, y no porque tu estes completamente equivocado… verdad?(…)» Como te he dicho, uno de mis problemas en la vida diaria es mi timidez, y siempre me ha costado decirle a alguien con más «credenciales» que se equivoca. No soy mala persona (aunque parece que te esfuerzas en que soy el villano perverso de la historia). Yo he soportado estoicamente como algunos me bloqueaban el twitter (incluso algún conocido de aquí) porque soy altamente apasionado con lo que me gusta y conozco. He soportado que a mis espaldas, en la lectura de mi tesina, un colega del máster dijera que mi frase «La detección del scaterring coherente de neutrinos en el SM es importante porque es background irreducible para los experimentos de detección de materia oscura» era incorrecta porque «El neutrino es indetectable», lo cual es completamente falso (el neutrino se detecta via Cherenkov effect, por ejemplo).
Soporté alguna risa sibilina de mi mi tribunal de tesina, pero bueno, no me puedo quejar, para haber escrito la tesis en 1 mes (cosa de estudiar y trabajar a la vez), un 8 no estuvo mal (aunque creo que me merecía un 9, el 10 no, acepto las reglas, tú no…) pero me sienta fatal la arrogancia como la que tú exhibes nuevamente en este foro bajo varias identidades. Pero ya me he dicho que no voy a admitir para nada que una persona como tú marrullera y con mil alias me diga que estoy equivocado en ciertas cosas. Yo admito mis errores, y mis ignorancias, tú hasta ahora NI JOTA. No lo has hecho. Cierto es que para saber hacer algunas cosas no hace falta título, pero el tenerlo nos hace estar cualificados para ejercer con ciertas «licencias». Tú hasta ahora lo único que has hecho es escurrir el bulto.
B) Deja de disfrazarte con mil alias para evitar que te baneen. ¿O es que piensas que cualquiera con imaginación, deductiva y ciertas habilidades no sabe quién eres? Tu problema es que quires aplicar a otros lo que no te aplicas a ti mismo. Aplicas dos baremos totalmente distintos según se aplique a ti o a los demás, y eso, Kac, no es admisible. Es hacer trampas. Aplicas dos raseros diferentes según se aplique a ti o a los demás: para ti no importan los títulos para argumentar o discutir, para los demás o en particular a mí mismo, estamos acusados de tener «titulitis» y nada más y nada menos que no podemos hacer argumentos sobre personas que son doctorando, postdoc, o doctores, pero que se equivocan (como todo el mundo). ¿O es que piensas que alguien como yo diría que la definición de gauging SUGRA es absurda sin saber de lo que habla? Más aún, lo que debería hacerte pensar es: ¿piensas que no sabía que mi ibas a sacar algún paper con algo así? Insisto, desgraciadamente para ti, no eres consciente de mis capacidades (bueno, deberías serlo), como nunca lo ha sido nadie que yo conozca (bueno, tal vez sí, algún amigo de USA).
C) A mí es muy fácil identificarme, siempre entro con el mismo alias aquí y en casi todas partes. Pero tú tienes un evidente complejo con el que intentas ponerte por encima de los demás bajo varias identidades, y también te ocupas de intentar hacer que la gente que a ti te parece (como Ynduráin, al que ni siquiera conociste) no sabe sobre algo (haciendo ciertamente asunciones que tú desconoces). Te pido que dejes de entrar con varios alias por aquí, y de enfangar via copy-paste e interpretaciones erróneas diferentes teorías de las que tú, siento decirlo, no tienes la más remota comprensión básica. Yo que tú, y perdona que te lo diga así, dejaría de ser tan «pared de frontón», porque al final, la más simple lógica elemental sirve para tirar del hilo. Finalmente es algo muy curioso, que tú sí te atrevas a intentar calificarme como persona, pero en cambio a ti no se te puede si quiera criticar. Además, es muy curioso que mis respuestas (las que te he dado, evidentemente no te he respondido más que a lo que me ha interesado) o bien «no te convencen», «las ignoras» o «las vuelves contra mí». Es curioso que insistas que qué busque que un paper concreto diga «double field theory» cuando te he insistido en que el término es de 2006 o más adelante, pero el concepto estaba ya en el trabajo de West, y si te empeñas, puedes verlo como consecuencia de la dualidad electromagnética o las propias teorías two-time physics de I. Bars. Estaban ahí en esencia, aunque claro, no bajo ese nombre, no bajo esta formulación que ahora se hace en DFT.
D) Al menos deberías tener la DECENCIA de entrar siempre no ya con el mismo nick, sino en plan menos fanfarrón y con más RESPETO. Si yo te he llamado TARADO o mentiroso es porque tengo mis razones (expuestas arriba) y porque ya has estado por aquí antes (¿a que sí?) con ciertas ideas ciertamente «asombrosas» pero que nadie en su sano juicio aceptaría. Te recomiendo que te centres en tus ideas (bien en las de tus blogs dispersos, o bien en las que dices tener, si es verdad que lo entiendes-cosas que dudo, porque yo no lo entiendo del todo, y si yo no lo entiendo, perdona que te diga que tú no podrás entender ni lo de la geometría generalizada compleja ni las excepcionales ni cualquier otra cosa de la que aquí has simplemente intentado exhibir conocimiento parcial que cualquiera que tenga tiempo libre puede tener). Es evidente que no entiendes las cosas que dices. Así que por mí, podemos dejar la conversación un tiempo.
PS: NO olvido lo que digo, prometo en unos días postear aquí el artículo en el que West sugiere duplicar los campos y una nueva simetría (que acabaría siendo años después lo que Hull y Zwiebach bautizaron como DFT). Sobre lo de los superespacios tensoriales extendidos, al igual que he hecho yo con tu misterioso KKLT, haz un poco de search and research, a ver si así tienes un poco de cura de humildad, que veo te sigue faltando, no has cambiado en eso. Sigues siendo igual de borde y prepotente que siempre (aunque lo disfrazas de perfeccionismo y de una falsa «educación» -modales- de la que careces).
Hola amarashiki.
1) Sin comentarios.
2) Si se que el grupo U-dualidad de las supergravedades cuatro-dimensionales no es Sp(2n,R). No obstante, el grupo de U-dualidad tiene que ser localmente embebido en Sp(2n,R) para que pueda ver una accion del mismo bien definida sobre los campos de la teoria. Esto es precisamente lo que digo en la definicion que doy. Asi que tu puntualizacion es incorrecta. La definicion, obviamente, no es absurda, has visto que figura en ese paper y se usa muchisimo en Teoria de Cuerdas y Supergravedad.
3) La DFT dobla las coordenadas, no los campos. Pero quedo a la espera de ver cual es la relacion.
4) Yo estoy dispuesto a responder a cualquier pregunta que este relacionada con lo que escribo. No a preguntas aleatorias que me haces para intentar probar que no se algo. Tranquilo, ya asumia que no me ibas a decir que es un «superespacio tensorial extendido», cuando tu mismo lo has nombrado.
i) No entiendo a que te refieres. Yo en ningun momento he dado importancia en este debate a los titulos que puedas tener tu o que pueda tener yo. Y ni siquiera se si tienes un PhD. o no, y no me interesa.
ii) Desde el principio he mantenido que KK y SS no se han abandonado, siguen usandose en Fisica. Pero vamos, tu a tu bola ;).
iii) Aqui dices muchas burradas.
«Además, la reducción dimensional que comentas, en términos técnicos, produce un (hyper)Kähler (super)potential que efectivamente tiene mínimos.»
Lo primero, el (hyper) sobra. Lo que hay es un Kahler potential, propio de cualquier variedad Kahler y a partir del cual se obtiene la metrica escalar, y un superpotential, que determina un sector de la teoria. A partir de estas dos cantidades (dependiendo tambien de que sugra sea), se puede calcular el potencial escalar. En N=2, por ejemplo, el superpotencial determina tanto el kahler potential como el sector de los vector multiplets de la teoria. Cuando el potencial es definido negativo, se dice que la compactificacion tiene como vacio AdS ya que el unico vacio de la Teoria (solucion maximalmente simetrica) es AdS. A eso es a lo que me refiero, no pense que fuera necesario explicarlo. El paper KKLT es muy famoso (tiene mas de 2000 citas), no pense que hubiera que dar mas detalles. Pero si me hubieras preguntad te lo habria dicho encantado. Y no he dicho (de nuevo, obviamente) que sea la panacea, solo he dicho que es el primer embedding de dS en Teoria de Cuerdas. Todo lo demas que dices y te montas es una paja mental tuya.
Finalmente: no se con quien me estas confundiendo desde hace rato ya, pero no soy esa persona. Y por cierto, no tengo ningun blog. Lo de la titulitis lo dije, claramente, a raiz de que desde el primer momento estabas exhibiendo tu titulo Universitario y de Master y los papers que leis en la Universidad y que cursaste todas las asignaturas del Master y todas esas cosas que no le importan a nadie. A mi me da igual si eres licenciado o tienes un master, yo por mi parte no exhibo mi titulacion intentando utilizar un argumento de autoridad. Has dicho muchas cosas incorrectas a lo largo del debate, pero no pasa nada, no somos expertos, solo aficionados, y seguramente yo las he dicho tambien. Lo peor de todo ha sido tu actitud cuando te he pedido aclaraciones sobre cosas que tu mismo has afirmado.
1) Si contradecirte tú mismo no te merece comentarios, insisto…Estás como una regadera. XD. No merece comentarios que te contradigas a ti mismo¿? Eso es ser muy consistente. :).
2) Incorrecto: tú definiste y variaste la definición textual del paper. El grupo de U dualidades de SUGRA ¿tienes que embeberlo en el grupo de de dualidad electromagnética? ¿Tienes alguna prueba de lo que dices? De hecho el grupo de U-dualidad no se comprende como embebido en el grupo simpléctico de dualidad electromagnética. No hasta donde yo sé del tema (no soy omnisciente). Además que en ese paper NO aparece el tema de la U-dualidad que mencionabas, y tu pusiste que la definición que tú dabas en el paper era la que decías arriba, y obviamente, no es la misma…Pero vamos, sigues erre que erre…Como esta, tú definición es absurda porque está sacada totalmente de contexto, y en el paper no dice nada de lo que tú has dicho arriba ( a no ser que identifiquemos tu definición y la del artículo, que no es posible; si lo es, dime un sitio donde venga exactamente lo que dices y ahí, entonces, puedo aceptar que tu definición de gauging SUGRA es válida).
3) DFT dobla los campos, ¿no me has leido arriba?¿Cómo se interpreta una coordenada de una supercuerda? Como una campo en la wordsheet ¿o no? Hoy he terminado con las imágenes, cuando termine con los apuntes ya me pongo a mirar lo de West, si te apetece vaya. La idea de West fue que si se duplicaba el campo gravitacional, por el asunto de la dualidad T, eso al final llevaría a duplicar también los otros campos (como pasó en el paper citado) si la simetría se extendía a ellos también. Insisto, West no lo llamó double field theory, pero si esperas a que pase los apuntes, intentaré buscarte la frase concreta de West pre- (Hull-Zwiebach) naming. ¿Estamos de acuerdo? Pero insisto, West no fuen quien dijo «double field theory» como tal (hasta ahí no llega mi memoria, no puedo asegurarlo) pero sí estoy seguro de que mencionó eso por los años en los que te he dicho.
4) a) Hombre, lo del superespacio tensorial extendido, ¿por qué te interesa? Además, insisto, puedes bucar lo que es tú mismo. No es demasiado difícil. No es un campo en el que trabajaran centenares de físicos (como en cuerdas). Digamos que en las modificaciones de la relatividad en las que yo andé, ando involucrado y estaré (si no pasa nada raro, aunque sea como independiente-hay algún documento mío por ahí, y se me cita en agradecimientos de varios papers, incluso desde mis tiempos de estudiante) son cosas en las que ando pensando (por eso no me gusta dar detalles, tanto técnicos como de otro tipo; privacidad primero). Yo sé lo que es desde tiempos de pregraduado. Te lo podría contar, y ciertas cosas que no son demasiado conocidas por mucha gente, pero que están empezando a salir (ayer salió un artículo en el arxiv sobre algo que posteé en physics.stackexchange, y me da rabia no poder estar en algún sitio para competir y que otros solamente desarrollan muy parcialmente). POr eso de algunas cosas, me cuesta más hablar, porque tocan cosas que sigo estudiando porque aún no están suficientemente entendidas ni son consideradas «aparatos usuales» como sí lo son otras técnicas matemáticas, como la reducción dimensional, supersymmetry… Volvemos al asunto de las modas… Es peligroso ir por donde van todos, pero también es ciertamente arriesgado intererse por temas avanzados que poca gente conoce. También puede aparecer alguien con más visión que tú (o no) y que haga un revival de tu idea y de repente te encuentras con competencia inesperada (ay, madre, los chinos…¡qué miedo!Y no es broma-en algunas charlas se comenta frecuentemente el asunto de sacar resultados antes que algún grupo chino de forma cada vez más frecuente). Pero insisto, no es difícil encontrar lo que es. Y dichas técnicas de superespacio tensoriales (en algunos casos con herramientas de twistores) pueden encontrarse fácilmente en la web. Tampoco voy a definirte algo que yo quiero actualmente redefinir y ampliar (como otras cosas) en el contexto de «otra cosa» que esta por venir. En especial, si como espero y deseo, hay null results de toda Dark Matter en detección directa (aunque el framework, como cualquier framework, es adaptable). En fin. Un poco de search and research no te vendrá mal.
4) b) Es curiosísimo, resulta que yo sí te tengo que responder a tus preguntas, pero tú no a las mías porque tienes la «excusa» de que lo hago para saber si sabes de lo que hablas (tengo mis dudas razonables, por eso pregunto). Ya te digo, no me interesa contarte lo que es porque tu simplemente has tomado a mala saña y para medirte mis cuestiones de arriba. Insisto. ¿Por qué debo contestar yo a toda pregunta técnica y tú a nada? Aunque claro, si estás empeñado en que lo hago para dejarte en ridículo… Tampoco te pongas así, porque yo sólo quiero saber hasta dónde puedo hablar.
El hyper no sobra, al menos en lo que quería decir (pero sí, de me colé con el prefijo, aunque no en lo que quería decir). Lo puse por las variedades hyperkähler que en ocasiones se usan (ahí se me soló el hyper para el potencial sic, pero es que lo hyper mola en física y matemáticas, y soy algo terrible con los nombres de persona y la terminología, prefiero hacer las cosas en papel o explicar lo que quiero decir con matemáticas o definiciones más concretas, en estos foros me he autolimitado a no soltar demasiadas definiciones hipertécnicas y sofisticadas o demasiadas ecuaciones poco conocidas). Se suelen preferir kahler manifolds a hyperkähler simplemente para compatificar, aunque la terminología matemática y física es sutil. Ciertamente para lo del potencial, la terminología hyper sobra (mea culpa ¿puedes reconocer tus fallos de vez en cuando?Hablo de lo del landscape y las Calabi-Yau, ahí patinaste un poco ¿oh no?Bueno, veo que al menos al final lo admites un poco)
5) Curioso: No pensaste que hubiera que dar detalles a la audiencia de Francis de un paper que citas por las siglas (toma) en un hilo de un foro de divulgación científica (que no es para nada un sitio especializado). ¿Por qué piensas que no pongo demasiadas ecuaciones por aquí? Piensa un poco. YO soy una persona sumamente calculadora. Y pese a lo que parezca por cómo me expreso, siempre sigo un «master plan» XD. El paper será conocido para ti, yo fácilmente le he recordado y le he ubicado, pero evidentemente, pese al número de citas que tiene. Ni panacea, ni será reconocido en general por «cualquier lector habitual». Por la tanto, al menos ahí reconoce que te has pasado de «listillo» ¿no crees? Y lo digo sin ánimo de ofenderte para nada (y lo digo en serio).
6) Explica esto mejor: «(…)Cuando el potencial es definido negativo, se dice que la compactificacion tiene como vacio AdS ya que el unico vacio de la Teoria (solucion maximalmente simetrica) es AdS. A eso es a lo que me refiero, no pense que fuera necesario explicarlo.(…)» Oooohhhhhh… ¿En serio? Dame una referencia de eso, por favor. Me refiero a lo que dices de cuando la compactificación tiene como ÚNICO vacío AdS es, el Kähler potential es definido negativo. Esa es una afirmación bastante más fuerte que cualquiera de la que hemos hecho. Referencia, pleeeaaaasssseeeeereeee, jajajajajaja :P….
7) Lo de que habías dicho que era dicho paper KKLT era » el primer embedding de dS en cuerdas» no es lo que habías dicho más arriba. ¿Tienes mala memoria? Arriba lo que habías dicho es que el «problema lo había solucionado KKLT», mencionas que el vacío es estable (era más precio haber dicho metaestable, pero vamos, no soy el único que mete la gamba con la nomenclatura ¿no crees?). Insisto, cualquiera que lea el paper, y te lo digo en serio, puede ver que es algo muy particular. Por supuesto que tiene muchas citas. Hay 3 pesos pesados de cuerdas, y el paper fue de los primeros que empezó a intentar seriamente acomodar un dS en cuerdas, aunque permita que siga siendo escéptico (supongo que me hago viejo). Pasa con esta idea algo similar o igual al modelo de Randall-Sundrum (RS), realmente estos modelos los inventaron otros antes, pero Princeton ya sabes el cobijo que te da… No se ha embebido aún en cuerdas de forma consistente ni se ha encontrado una solución de la teoría que contenga dicha métrica no factorizable. Es una construcción «de branas». O al menos no con técnicas usuales (que yo sepa) se ha logrado encontrar una solución de supercuerdas que dé una métrica RS en 5 dimensiones. Y es gracioso, porque RS es posiblemente un ejemplo de otra cosa que «encaja» dificilmente el framework de cuerdas usual pero que también pide a gritos AdS/CFT. No obstante, RS no parece a priori relacionado con el universo observable. Históriamente, ha sido otra vuelta de tuerca al escenario de extra dimensions que se propueso para solucionar el problema de la jerarquía (la disparadad de la masa de planck-o de la cuerda- con la escala de la gravedad a baja energía). La métrica «podemos decir rara» Randall-Sumdrum es una geometría no-factorizable que las teorías de supercuerdas tienen difícil de «encontrar» como solución (hay ideas, relacionadas con Finsler geometries y otras extensiones de la geometría riemanniana estándar que han intentado comprender RS). En resumen, tu habías dicho que el problema lo resolvía ese paper y yo te digo que para nada. Y lo de embeber en cuerdas dS, bueno, eso sí, pero sumamente forzoso (en mi opinión). Y eso no era lo que habías dicho arriba, que lo solucionaba. Luego has cambiado (supongo que porque te habrás dado cuenta de lo que dice y no dice el paper, y de lo que hacen y no hacen en él, digo yo) a un simple embedding de cuerdas. Es simplemente una matización y corrección.
8) Las pajas mentales que yo me haga o no, o más bien las cosas que yo piense son cosa mía. No deberías meterte con eso, de igual forma que no deberías juzgar lo que una persona a la que tú no conociste sabía o no de cierta cosa.
9) Pero sobre lo de la titulitis, …Uno de los problemas de este país, aparte de desperdiciar el talento de miles de personas que se exilian otras que están donde no deben estar por capacidades, es que tenemos gente incompetente dirigiéndolo (supongo que ahí me darás la razón). No digo que haya que estar licenciado para gobernar, pero está claro que si la clase política es inculta, y poco preparada, no se puede esperar mucho de ellos. ¿Se puede esperar mucho de unos gobernantes que no tienen cualificación en los ministerios o asuntos que manejan?
No entraré a juzgar si es necesario o no el papel (mis conocimientos no están en dicho papelito), simplemente te digo que al menos deberías respetar los que tenemos cierta educación (el papel es papel, y ciertamente hay cosas de los títulos que poseo que no dicen esos mismos papeles). ¿Hay que valorar más o menos la opinión de un «experto»? Pero yendo al grano, que me enrollo, me sentó mal que sacaras la titulitis porque yo siempre he pensado que si se forma a X personas en cierto algo, lo normal, en un país que funcione, es poder colocar a esa gente en lugares adecuados, sea la docencia, la investigación o tal,…No por el título, no, sino por la preparación o esfuerzo que nos supone ganarlos, y lo que ha supuesto al Estado que hayamos estudiado (yo más por mi cuenta, la verdad y más cuando el estado me denegó la beca el segundo año allá por el 98 por algo absurdo y tuve que ponerme a trabajar para pagarme mis estudios, lo que causó una bajada de calificaciones y me obligó a prolongar el tiempo en la uni y no a reducirlo como quería). Si tengo «titulitis» no es por el papel (que a mí me la repanpinfla: los tengo metidos en el armario y no colgados ¿sabías?) sino por lo que me costó obtenerlo mientras adquiría conocimientos de máster durante mi carrera y me aburría en los exámenes. No es el papel, no…Es el esfuerzo que yo dediqué a ser la persona que soy ahora. Si te dijero que el título no importa, pero que soy físico, pero que no me gusta que se cuestione lo que he invertido en ello (mi dinero y mi esfuerzo) espero me vieras de otra forma distinta. Si quieres, soy un físico que no trabajo remunerado por ello, pero como todos ellos, tengo mi amor propio. Si soy físico, como otros antes que yo, mi opinión vale algo (sobre todo por lo que pueda conocer y no conocer, y porque supuso una esfuerzo obtener ese papel, que parece ser ni tú ni nadie en este pais valora; pero bueno, es una discusión diferente esa tal vez). A la gente preparada se la exilia o se la hace trabajar en cosas ridículas, mientras que a los poliicos no se les exige nada (y así nos va y salen los que dirigen). Digo yo, que para algo debería servir (en España no, al parecer). Si saqué y saco algo de mi particular historia era para demostrarte que a mí también me la suda que seas o no físico, pero sí que te arrojes cierto conocimiento sin encima que yo pueda testarlo ¡! Por eso estoy algo enfadado ( virtualmente, no realmente, porque eso no afectará a mi vida cotidiana, que tiene otras urgencias). Además, cuando te comenté, para ponerte a prueba, lo de que yo siempre he tenido timidez de decir que algunos se equivocaban (en pasado), gente con post-doc o doctorados /profesores de Universidad, entiende que saltara como un resorte cuando tú me dijiste y me sugirieras que yo me equivocaba (al menos en las circunstancias de las que yo hablaba o pensaba) asumiendo de nuevo conocimiento de terceros (como hiciste de Ynduráin). Digo yo que sabré yo si estaban equivocados y yo no, como con Ynduráin. Tú no estabas allí ni los has conocido ¿verdad? Por cierto, yo cometí errores en mi máster, que asumí. Otros, no asumen los suyos (ni siquiera en el mundo virtual, porque puse en aprietos no hace demasiado tiempo a un Ph.D americano y a un propio cosmólogo senior por simplemente señalarles unos error en un problema).
El aludir a mi titulación no es para darme un halo de autoridad, que te quede claro, simplemente la exhibo porque digo yo, que si soy físico (aunque me dedique a otras cosas para sobrevivir por el momento, espero no siempre) teórico, y tengo un máster, haya papel o no, tengo cierta formación. ..Digo yo, pienso, creo, que eso me da todo el derecho del mundo a poder opinar de un tema de física teórica (incluso si no soy experto, pero lo he estudiado tangencialmente en alguna ocasión) con una opinión de diferente peso a la de una persona corriente a la que puedas encontrar en un foro usual. ¿O me vas a decir que la opinión de un «especialista» sin ser «hiperespecialista» tiene el mismo valor que una opinión «layman» o alguien «medicina general»? Hagamos una analogía con el dentista. Una profesión hoy tan especializada con la propia física: está el dentista de consulta «general» que te hace los arreglos menores, los ortodoncistas. Evidentemente la titulación cuenta (supongo) pero también lo que tú puedas saber o no (y para eso están los másteres, lo que puedas por supuesto aprender con internet, otros cursos online, youtube,…). Por eso me enojaba con tus negativas, y por eso no te respondía ni te respondo también directamente a los de los superespacios tensoriales (yo he trabajado con ellos porque le pedí por correo hace algunos años, mientras era estudiante, artículos originales de una de las personas que los inventó), algo a lo que le dediqué mucho tiempo escapándome de clases aburridas… Y algo con lo que me divierto intentando encontrar la teoría que ando intentado armar para (I wish) mi futura tesis doctoral (aunque al paso que voy, y sin contactos, creo que nunca 🙁 lograré la teoría con la que sueño, pese a todas las matemáticas que he ido aprendiendo en los últimos años)…Jajajaja…¿Me explico? Digo yo que alguien como yo podrá opinar sobre lo que alguien tú sabe o no, si responde a ciertas preguntas, no si las evita justificándolo en no sé qué postura. ¿No crees que es normal que quiera saber lo que NO sabes? Te he estado estudiando y midiendo desde el principio. Siempre lo hago con todo el mundo. Lo malo es, que como esperaba, tú te lo has tomado como si quisiera dejarte en ridículo… NO comprendes mi jovial espíritu comentarista, jis jis.
La actitud que dices yo la he tenido, ha sido porque tú empezaste a vacilar y fanfarronear ¿o acaso lo niegas? Además de que te metiste de mala forma con una persona a la que tú no has conocido y yo sí…¿Tengo que copiar y pegar los comentarios de tu twitter? Y lo digo de verdad, decir que Ynduráin no sabía de cuerdas porque decía que eran ficción ciencia es no haberle conocido. Por supuesto, podrías estar o no de acuerdo en sus razones (diferentes a las de Feynman), pero ciertamente no eran razonamientos para tú dijeras de él con toda la geta, en plan «stringer radical» (perdón si hay algún forofo y apasionado stringer follower aquí) que no tenía ni idea de cuerdas (nota mental: en tu twitter dices eso, como queriendo defender la teoría de cuerdas, pero luego también sueltas que la teoría está de capa caida y que te parece poco elegante; no pareces muy consistente o al menos no se sabe muy bien tu opinión al respecto de SUGRA o superstrings)….YO he dicho varias veces en este blog que mi pasión por las supercuerdas murió hace bastantes años. Reconozco sus virtudes (que son generalmente metidas por los ojos por muchos de sus absolutos incondicionales) y sus méritos, pero como Feynman o mi antiguo profesor Paco Ynduráin, también las critico. Al final será el experimento dirá qué nivel de realidad tienen, pero hay que saber, como teórico, los pros y los contras de las teorías y modelos que se proponen.
¿?¿? Yo he reconocido mis errores. Pero yo no soy un «mero aficionado» (otra cosa que no garantizan los títulos es la calificación respecto a tus capacidades en relación 1-to-1; no siempre al menos; por eso soy consciente de que no son requisito; tampoco dan trabajo y sustento por sí mismo; al menos no aquí en Xpain). Ni creo lo seas tú totalmente (aunque desde luego eres bastante petulante y se te escapan demasiadas coletillas) aunque se te da muy bien vacilar al personal y marear la perdiz, y exhibes algunos conocimientos superficiales más o menos detallados de algunas cosas. Pero eso da igual. Al final, lo interesante es saber si dices algo más o menos profundo, y no como otros (sean tú disfrazado o no; realmente, tampoco me preocupa porque eso no soluciona la ecuación de mi vida, jejejej; simplemente esto me lo tomo como ejercicio práctico para «mis otras habilidades», que no definiré aquí).
Y con esto, imaginando a Shakespeare en la comedia de «Un sueño en una noche de verano», te propongo que lo dejemos aquí, hasta que yo pueda retomar el «caso West». ¿De acuerdo? Lamento que te lo tomes de esta manera, pero reconoce que no todo lo que he dicho de ti es equivocado, y tú sí casi todo de mí.
Saludos. :).
En cuanto a la U dualidad y el grupo simplectico:
«De hecho el grupo de U-dualidad no se comprende como embebido en el grupo simpléctico de dualidad electromagnética.»
http://arxiv.org/pdf/hep-th/9605032v1.pdf Ecuacion (3.21) en adelante. Embeber el grupo de U dualidad en el correspondiente grupo simplectico es una tecnica estandar en Sugra para obtener la accion del grupo de U dualidad en los campos asi como los correspondientes acopolos. Lo del gaugeo no merece mas comentario, he utilizado la definicion estandar que se usa en el campo y tu la has calificado erroneamente de absurda.
«Se suelen preferir kahler manifolds a hyperkähler simplemente para compatificar, aunque la terminología matemática y física es sutil.»
Toda variedad hyperkahler es kahler, asi que parece que no tienes mucha idea de lo que hablas. De hecho, estas confundiendo el espacio de compactificacion con la variedad escalar resultante que parametriza las deformaciones de dicha variedad de compactificacion. Por ejemplo, para ir de la IIB a N=2 Sugra en 4d se puede compactificar en un Calabi-Yau manifold, que de nuevo es una variedad Kahler. Sin embargo la variedad escalar es el producto de una variedad Special Kahler y una variedad Hyperkahler (en realidad quaternionica, pero bueno, a este nivel «da igual»).
En cuanto a KKLT, la cita iba dirigida a ti, no a un lector tipico de este blog, y por la vagueria de no querer buscar el correspondiente arxiv, puse solo KKLT, asumiendo que sabias que era. Y me reafirmo en lo que dije al respecto: soluciono el asunto de embeber dS en ST. No digo que sea una solucion completamente satisfactoria, y soy consciente de que hay mucho research en es ambito.
«Oooohhhhhh… ¿En serio? Dame una referencia de eso, por favor. Me refiero a lo que dices de cuando la compactificación tiene como ÚNICO vacío AdS es, el Kähler potential es definido negativo. Esa es una afirmación bastante más fuerte que cualquiera de la que hemos hecho.»
Yo no he dicho que cuando el Kahler potential es definido negativo el unico vacio es AdS. De primeras, porque el Kahler potential no es ni definido negativo ni positivo, ya que es una funcion compleja y por tanto tal concepto no esta definido. Lo que he dicho es que cuando el potencial escalar (que se construye a traves del Kahler potential y el prepotencial) es definido negativo, el unico vacio es AdS. Esta cuestion es muy basica, asi que te la puedo demostrar por palabras:
El vacio de una teoria clasica de campos (como la sugra) es una solucion maximalmente simetrica con los campos sin excitar. En concreto, los scalares son constantes y por tanto el potencial escalar actua como una constante cosmologica negativa, ya que esta definido negativo. De manera efectiva, queda un sistema que es simplemente RG + cte cosmologica negativa, y la unica solucion maximalmente simetrica de dicho sistema es AdS.
» O al menos no con técnicas usuales (que yo sepa) se ha logrado encontrar una solución de supercuerdas que dé una métrica RS en 5 dimensiones. Y es gracioso, porque RS es posiblemente un ejemplo de otra cosa que “encaja” dificilmente el framework de cuerdas usual pero que también pide a gritos AdS/CFT.»
RS si que ha sido realizado en Teoria de Cuerdas (hay que informarse un poco mas antes de soltar esas pedradas). En el siguiente paper se hizo por primera vez:
http://arxiv.org/abs/hep-th/0105097
Las preguntas que yo hago estan directamente relacionadas con lo que afirmas. Ya sabia yo que no me ibas a explicar lo que es superespacios tensoriales generalizados, que tu mismo nombraste, porque dudo que sepas que significa. Me reafirmo en todo lo que he dicho de ti; lo que tu has dicho de mi sencillamente me da igual :).
«en estos foros me he autolimitado a no soltar demasiadas definiciones hipertécnicas y sofisticadas o demasiadas ecuaciones poco conocidas»
Pues conmigo puedes soltarte un poco, intentare seguirte. Ya que tu has repetido tantas veces tu titulacion y terminamos aqui el debate, te dire algo sobre la mia. Soy Matematico (doctor) en el ICMAT, y trabajo actualmente en temas de Fisica-Matematica, en concreto en aspectos matematicos de la Teoria de Cuerdas (Generalized Complex Geometry y Exceptional Generalized Complex Geometry). De hecho, creo que ya he caido en la cuenta de quien eres, y debo decirte que hemos asisitido juntos a algunas clases del master de Fisica Teorica que tu cursaste (no dire donde por si no quieres hacerlo publico).
Que como era de esperar, tiene un porron de citas.
Me alegra que al final soltaras quien eres. :). Al menos así sé con quien hablo (tengo la mala costumbre de dudarlo por el cibermundo por diversas experiencias pasadas). :). Digamos que en ocasiones :). Es evidente que coincidimos en la UAM. (Cualquiera puede hacer la deducción sabiendo donde daba clase Ynduráin). Siento haberte picado tanto. :). Tuve otra discusión hace un tiempo con otras personas que soltaba cosas algo más que absurdas. (NO como lo tuyo, aunque ciertamente, algunos comentarios me vuelven algo malpensado, en especial, cuando hablas de personas que no yo creo no conociste). Ya te paso mi mail por twitter y discutimos las cuestiones técnicas por gmail si lo prefieres. ¿Te parece? Francis no querrá que inundemos esto de formalismos varios. ¿Qué opinas?
Prefiero seguir hablando por aqui. No entiendo cual es la relevancia de «saber con quien hablas» en una discusion de Fisica. Lo unico relevante es lo que se dice y lo que se demuestra, no importa quien lo diga. Soy la misma persona sobre la que dijiste (entre otras cosas)
» perdona que te diga que tú no podrás entender ni lo de la geometría generalizada compleja ni las excepcionales ni cualquier otra cosa de la que aquí has simplemente intentado exhibir conocimiento parcial que cualquiera que tenga tiempo libre puede tener»
«YERRAS por enésima vez, demostrando que no tienes ni pajorera idea de los que es la dualidad U en SUGRA»
«Es evidente que no entiendes las cosas que dices.»
«TARADO mental»
asi que no veo el interes de una conversacion privada contigo. De hecho, ya que este hilo ha sido inundado de cuestiones personales, creo que ahora mas que nunca debemos continuar debatiendo por aqui si vamos a hablar de Fisica, ya que es lo que puede interesar a los lectores que entren en este articulo. Y por favor, no escatimes en tecnicismos, no creo que nadie los encuentre inapropiados, Francias el que menos.
Me apunto a lo de seguir hablando de Fisica, pero por favor que sea de manera constructiva y no a base de tecnicas de debate -que a mi, personalmente, me parecen rastreras-. Puede que no te des cuenta, pero la combinacion de preguntar y ocultar informacion sobre lo que sabes suele ser equivalente a dar cuerda para que el oponente se enrede él solo. Indica que, consciente o subconscientemente, se esta pensando en terminos de oponentes, sean dos equipos que se forman para hablar a favor en contra de un tema, o sea el típico alumno con la pregunta capciosa preparada para pillar desprevenido al profe, el equivalente a un troll en el aula. Siempre es mejor eso que el silencio absoluto, pero no es la mejor opcion.
En cuanto a saber con quien hablas, eso sigo sin saberlo y en efecto no importa, incluso si eras un bot o un grupo a lo Bourbaki o Luther Blisset. Pero sí que tiene relevancia saber desde dónde te hablan. Puedes ser mas preciso con la bibliografia si sabes que no estas limitado a referirte a lo que encuentres en el Arxiv. Y se esta más atento a algunas variantes de nomenclatura; por ejemplo, aunque suene ridiculo, yo tiendo a decir KK theory si hablo con un físico y Kaluza-Klein theory si hablo con ciertos matematicos, por miedo a que se confunda con Kasparov K-Theory. Sí que es cierto que al ser este un medio publico y estable, tendriamos que considerar que puede haber otros lectores, no solo ahora, sino dentro de cinco años.
Dicho todo esto, confieso que no sé que parte del largo intercambio entre vosotros puede ser relevante al topic del post y desde donde podriamos seguir. Por mi parte creo que las dudas explicitas que han salido las he contestado todas; me apeteceria indagar un poco mas en lo de si hay alguna posibilidad de aprovechar el teorema de Arnold, Masser y Kuiper para construir alguna tecnica de compactificacion que evadiese todos estos dichosos non-go. Tambien me apeteceria discutir Kaluza Klein en D=9 y su posible uso para construir simplemente una teoria de electromagnetismo y color.
Sobre por dónde podríamos seguir, creo que la idea sería si las teorías KK y la SUGRA en D=11 tienen opciones futuras reales de explicar el espectro de masas del modelo estándar Y proporcionar un vacío dS que se asemeje a nuestro universo (que ciertamente, según lo que parece por los datos del LHC está muy cerca de la «metaestabilidad»).
Y más si no aparecen nuevos «campos» que predicen estas teorías en el LHC…
Alejandro Rivero tiene muchas ideas. Todavía no lo he conseguido incluirlos en un modelo, pero he aprendido mucho. Hoy su ensayo da una nueva dirección nuevo:
http://abjam.wordpress.com/2013/08/21/phenomenology-and-theory/
KacMoody y amarashiki y otros teóricos podrían probarlo. 🙂 Investigar utilizando sus ideas favoritas (Generalized Geometry, BPS preons?). Incluso si usted no encuentra ningún modelo, usted todavía aprender algo.
Me disculpo por cualquier error en mi cyber-castellano.
Hi Mitchell, sorry I did not tell you about the previous post! I had some interest on trying to explain myself in Spanish, at least to detect other sources of misunderstanding, and Francis allowed me a guest post in his blog. This other entry is already entirely of his own, but we have hijacked the comment thread 😉
Personally, I don’t think Alejandro’s ideas are worth pursuing. That is not research in particle physics and you can’t make a research paper from it.
Yeah, but on the other side, theoretical physics branched out of being research in particle physics at about the end of the seventies, so you can not make science from it neither.
OK. Entonces, y públicamente, me disculpo por dichos comentarios (supongo que no socializar demasiado me vuelve inestable en las redes sociales con frecuencia, aunque cierto es que tiendo a «exagerar» mis reacciones y mis palabras para producir los efectos que deseo). Obviamente, alguno de ellos pasados de tono y sin razón, pero tenía que cerciorarme de si hay alguien que entienda lo que dice detrás.
Y algo que he aprendido en los blogs es de vez en cuando a ser «controversial» para poder discernir mejor si alguien sabe de lo que habla (aunque me enojó que hablaras de otras personas como si las hubieras conocido) y llamar la atención. Sobre lo de si entiendes o no algo, se demostrará por lo que discutamos aquí continuando el hilo.
Ciertamente prefiero las discusiones puras de Física o Matemáticas. Apartemos todo lo demás, ciertamente si a ti te importa poco lo que he dicho de ti, tampoco pensarás que yo me he tomado en serio todo lo que has dicho tú de mi. Para poder afirmar ese tipo de cosas, la única manera es conocer a alguien en persona, y con pizarra o papel, comprobar ciertas cosas.
En cuanto a las discusiones de Física, espera que termine con los apuntes de Física que ando desesperado por LaTeXear (ayer por fin, tras varios días, terminé) para las cuestiones más técnicas (¿tienes paciencia?¡Seguro que sí! :)), te respondo aquí sólo a las conceptuales para aclara cosas. Ayer terminé de cambiar las imágenes de mi blog (ha sido un poco pesado la verdad, pero h elogrado hacerlo más rápido de lo que pensaba). Por otra parte,…Todos podemos equivocarnos en forma y actitudes, supongo estarás de acuerdo, como yo lo estoy en lo que dices de que al final lo que importa es si sabemos lo que decimos y sabemos (déjame añadir, que yo diría también si admitimos lo que NO sabemos, porque lo que importa es también lo que NO se sabe, casi más que lo que conocemos ¿estás de acuerdo?). Y también en que de nuevo me han podido las formas.
(Inciso: Perdón Francis, me ha vuelto a pasar: soltar exabruptos. Intentaré controlarme más, incluso y no equivocarme sobre quién es o no un troll, un poco con algunos por aquí que sueltan perlas).
Intentaré ser ordenado:
1) Lo del tema del «gauging de SUGRA». Es cierto lo que dices. Ahí confieso que me sorprendiste, porque yo no conocía tal definición en conexión al grupo simpléctico. Aunque insisto en que la realización del «gaugeo» de cualquier teoría de supergravedad (o en general cualquier teoría gauge) es cuestión del grupo gauge. Aunque sigo sin estar de acuerdo en que el grupo de U-dualidad sea ese grupo simpléctico que mencionas (que es de dualidad electromagnética). Insisto, tal como lo decías, no era una definición tal cal. Y el grupo de dualidad electromagnética no es el mismo que el de U-dualidad. Yo entiendo el grupo de U-dualidades de teoría M no es ése. Aquí, seamos francos, quizás es una cuestión de nomenclatura como en nuestra discusión sobre lo que es una teoría gauge (creo que ambos sabemos la definición, como que gravedad no es una teoría YM; quizás sea algo como lo que dice Wilczek, pero es sólo una conjetura).
2) Asunto RS. Ciertamente, es verdad. :D. Confieso que eso lo puse como prueba (ya que no respondías a otras, solté algo que no es verdad, a ver si saltabas). Yo hablé con A.M.U. en la mi licenciatura antes de la fecha del paper que mencionas porque era un problema a solucionar por aquel tiempo 1999 ó 2000 (los papers de RS son del 98-99¿?, aunque esos modelos ya eran conocidos por otras personas, fueron Randall y Sumdrum quienes los pusieron de moda). En aquella época yo era MUY prostrings y branas, y era un problema de entonces (no de ahora) el lograr obtener esas geometrías desde una perspectiva de cuerdas….Embeber RS en cuerdas es posible desde hace algunos años, sí :). Aunque, no es fácil ¿verdad? Hay que usar herramientas «complicadas». Y puesto que tú trabajas en el área de geometría generalizada, sabrás de eso mucho más que yo.
3) Me alegra ver que reconoces que el paper de KKLT no es una solución definitiva al problema de lograr un vacío AdS estable (no metaestable) o suficientemente estable (metaestable) en teoría de cuerdas y supergravedad. Pero así no lo dijiste al principio (lo del embedding, digo), ¿correcto? Quiero decir, que luego reculaste un poco, pues inicialmente, al final de tu párrafo tras el punto 7) de tu comentario inicial tras el de Laura dijiste simplemente:
«(…)Lo dificil es lograr un vacio dS estable y demas: tal problema fue solucionado por KKLT.(…)»
Tal enunciado, como tal. Es sumamente impreciso a lo que luego, cuando te cité la referencia, dijiste.
Sólo un par de cosas: decir que no diste la referencia por vaguería y tal, y que yo lo miraría, es ciertamente sorprendente, …Aún más cuando lo de KKLT lo soltaste en tu segundo comentario de este hilo, sin que aún me hubiera metido yo aquí, y sin una referencia explícita a que iba dirigida a mí. ¿Sabías que iba a entrar al trapo? En twitter no lo mencionaste, así que yo no tenía NI idea de que tal comentario iba para mí. Simplemente tenía curiosidad en si tal paper hacía lo que decías, y en el arxiv acoté la búsqueda con lo que recordaba de dS incorporando como autor a RK, cuando leí el abstract, ya recordé que había leido ese paper hace tiempo. Te diré que no dices en ningún lado que fuera dirigida a mí de forma explícita. Eso lo has dicho ahora y ciertamente ¿pretendías que supiera que iba dirigida a mí? Simple curiosidad, eso significa que tu también intentas anticiparte las reacciones futuras, como hago yo. Es es muy de jugador de ajedrez.
4) Asunto «superespacios tensoriales extendidos» (Azcárraga et. al.), asunto West/DFT , y asuntos técnicos para cuando tenga tiempo de responder con precisión y pueda editar matemáticas y definiciones suficientemente precisas para lo que quiero decir aquí. ¿Estamos de acuerdo? (Espero que en unos días, I wish; pues a fin de mes/inicio de septiembre, será cuando retomaré, espero, los posts de mi blog también, tras la migración y los cambios cosméticos e internos que ando haciendo a ratos).
Un cordial saludo.
Varios errores:
— «un vacío AdS estable» … «un vacio dS estable» Upps, una de esas es una errata, o esta mal redactado.
— Kac-Moody, el nickname, es un troll, al parecer no de internet sino de la variedad academica. De hecho el primer calenton te ocurrio en twitter despues de la pregunta trampa del numero de componentes del fermion.
— Azcárraga me parece que no el actual es presidente de la RSEF. Leo que se presento a vicepresidente. Anda, que menudo lio de retorica os habeis armado ahi.
Y digo lo mismo, a ver si poco a poco podemos centrar la danza de nuevo sobre Kaluza Klein. Pienso que estabilizacion y KKLT tiene demasiada miga para los comentarios, pero bueno, si os interesa tirad por ahi, yo voy, como se suele decir, a comprar palomitas para ver el espectaculo.
Sí, es errata al escribir, el KKLT me refería a dS, pero vamos, yo soy escéptico respecto a cómo surgen AdS y dS «estables» embebidos en ciertas teorías de supercuerdas y supergravedad.
Sobre Azcárraga, yo pensaba que se presentó a presidente y había ganado (es lo que me comentaron). Puede que la persona que me lo dijo estuviera equivocada y está de presidente. Como no sigo eso, tampoco tiene demasiada relevancia su puesto, sino su trabajo en supergravedad, geometría diferencial, grupos cuánticos y otros campos. A mí siempre me encantó su forma de entender la SUGRA y su estructura (él fue pionero junto con Townsed de la introducción por ejemplo, de las cohomologías de álgebras de Lie en Física Teórica, así como de otras varias herramientas). Además él trabajo como pionero en los superespacions tensoriales extendidos que mencionaba junto con algunos rusos de forma independiente. Creo sin embargo, que su propuesta de los BPS preons como grados de libertad fundamentales de M-theory no cuajó. Al menos, esa idea como tal, no ha sido continuada.
Sobre por dónde seguir, en relación a lo de Francis, otra opción es pensar si el escenario de compactificaciones, incluso si pudiéramos entender todas las matemáticas y espacios, bien el tradicional de KK o el actual, desde SUGRA o M-theory lleva a algún lado. Está claro por el problema del landscape y por otras razones varias, que no hay forma unívoca de reproducir no ya el dS Universe en el que vivimos, sino SM plus gravity. Haciendo el paralelismo con SUSY (sea a baja o alta energía), en la versión MSSM, que puede ajustarse a los datos del LHC como el SM. En cualquier escenario de reducción dimensional desde M-theory, SUGRA o superstrings aparecen campos que de momento no «observamos». Igual que los campos extra del MSSM son un añadido que es virtud y problema.
Alejandro, la pregunta sobre las componentes de un fermion no era ninguna pregunta trampa. Simplemente dijiste que un fermion tenia un numero de componentes que no me cuadraba, y pregunte para enterarme de a que te referias.
Bueno, si es asi retiro lo de troll.. aunque mantengo lo de academico :-D. Es cierto que la cague al intentar dar más efecto, normalmente se dice al reves, algo asi como «El 44 son las componentes del gravitón en D=11; 128 son las componentes de un campo fermionico; por tanto faltan 84 componentes bosonicas»; en ese caso, y siendo que se esta hablando de SUSY, todo el mundo asume que estamos hablando del gravitino aunque te saltes decirlo.
Más constructivo, pienso yo, habria sido preguntar «¿por qué no usamos fermiones más pequeños, en vez de uno que nos obliga a compensar tantas componentes?». En fin, son cosas de estilo y de que no estoy acostumbrado a la exposicion publica; me vienen bien para ver mis fallos.
Por cierto que me gustaria entender un poco mas de esta tripleta (44,128,84) y en particular del 84, que normalmente se vende como la source para la 2-brana, pero entonces, ¿que pasa con la 5 brana? ¿Hay una tripleta dual, con un 84 que es fuente de la 5-brana y otro 128 y otro 44? ¿O es la misma?
1) «Aunque sigo sin estar de acuerdo en que el grupo de U-dualidad sea ese grupo simpléctico que mencionas (que es de dualidad electromagnética)»
Yo no he dicho que el grupo de U-dualidad sea el grupo simplectico Sp(2n,R), relee lo que he escrito y no tergiverses mis palabras. He dicho que el grupo de U-dualidad esta localmente embebido en el grupo Sp(2n,R) para que actue consistentemente en los campos de la Supergravedad y para obtener los correspondientes acoplos.
2) Como comprenderas, es ridiculo decir que me pusiste eso como prueba, pero bueno dejemoslo ahi.
3) Me reafirmo en lo que he escrito. KKLT soluciona el problema de embeber dS estable en Teoria de Cuerdas, y lo solucionan explicitamente. Tecnicamente, no es estable sino metaestable, pero es un detalle menor. Esto no quiere decir que ese paper sea la solucion final de la descripcion de dS en Teoria de Cuerdas, pero si resuelve el gran problema de si se puede obtener dS en Teoria de Cuerdas afirmativamente.
4) OK.
Hola, álgebra de Kac-Moody :). Voy a esforzarme mucho más que antes en ser ordenado y preciso, ya que eres matemático físico.
Cuando comentabas la definición de gauge de gravedad, tu definición fue la siguiente (para aclarar el punto)
«Gaugear una Supergravedad es escoger de manera consistente un subgrupo de isometrias de la variedad escalar embebido en el correspondiente grupo de U dualidad»
Son tus palabras textuales arriba y luego nos remitiste al paper del 96 arriba citado, página 3 y a una sección del mismo. No tergiverso nada ni es mi intención hacerlo. Simplemente digo que tu definición no es tal cual aparece en ese paper. El grupo mencionado en el paper al respecto de gaugear la SUGRA no es el de U dualidad sino el del «primo» electromagnético. Pero vamos. Ya comprendo lo que dices sobre gaugear SUGRA. La definición como tal de esa forma la desconocía (no podemos saber toda definición o terminología, por eso te pregunté qué entendías tú por gaugear, si dije que era absurda ya te he dicho por qué lo hice antes, ahí desde luego me pasé de la raya). De ahí la importancia que tenía para mí aclarar lo del gaugeo (Alejandro también lo mencionó con otras palabras) y la elección de grupo gauge ( a la que antes me he referido).
2) ¿Qué es más ridículo, o mejor, más «curioso»-creo que es una palabra mejor porque no tiene interés ni objetivo despectivo mi elección?¿Que te puse eso como prueba y lo diga como tal, sin esconder mis intenciones- o que pusiste las iniciales del paper KKLT y por vaguería no lo citaste presuponiendo que yo sabría que iba dirigido a mí el comentario cuando ni siquiera yo podía saber que iba a mí? Ambas acciones demuestran lo mismo: la presunción de que dadas dos personas A y B van a tener cierta reacción ante algo que se escribe. ¿No crees? Son igualmente sorprendentes porque ambas evidencian que buscábamos ciertas reacciones y presuponen «a posteriori» lo que iba a pasar. Pero estoy de acuerdo contigo. Dejemos esta discusión espúrea aquí, porque no soluciona para la nada las cuestiones de fondo de Física y Matemáticas.
3)Bueno, ahí discrepamos (supongo soy más físico que matemático en este caso). Yo no veo tan claro que la construcción de dS en strings «funcione» siempre o que sea tan «natural», como parece tú sí que sostienes (dado que mantienes tu postura). Podemos discrepar en esta cuestión, supongo. Mi queja con RS es similar no te creas. Son embebible en cuerdas, pero el precio me parece «elevado». Supongo que «soy un viejo»(no tanto, 7⁵ en formulación «tropical», creo). Como he dicho, es importante y el artículo está bien escrito, aunque hace un montón de asunciones y requiere mucho «hilo fino», no sé si me entiendes. Alguien más listo que yo (hay mucha gente) dijo que todo depende de los prejuicios que se tengan. Mi impresión es que tal cosa (el embebding tanto de RS como de dS) no es natural, sino artificial y «forzada» en las formas de ambos papers las «introducen» (la estabilidad en el caso dS me parece la más importante, y las hipótesis necesarias para lograrlo, mientras que para RS me parecen aún poco naturales-quizás porque no soy experto- dichas construcciones). Por supuesto, está basado en matemáticas sofisticadas, y no dudo de lo que se hace. Pero, aparte de que como tú mismo mencionaste arriba (aunque yo insistía en ello antes), quedan problemas importantes no resueltos para un construcción «dirigida» (con valor, sin duda) en el caso de dS. Además, como he dicho, mi impresión es que no es demasiado práctica y «manejable» en el sentido de que nos permitiera, por ejemplo, determinar algún parámetro cosmológico (para eso queda mucho, mucho, se está demasiado lejos). Sí, puede construirse algo que se parece al Universo, pero un sin fin de problemas quedan no resueltos en tal construcción. ¿Solución final? No, en eso estamos de acuerdo. Pero al embedding le criticaría la forma de hacerlo y el resultado obtenido para la cota de tiempo de vida (metaestabilidad). ¿Algo nos garantiza actualmente que la construcción de KKLT no pueda ser realmente inestable por algún efecto cuántico que no hayamos tenido en cuenta? Insisto en que al obtener dS tenemos QFT en curved spacetime, y en mi opinión, eso introduce muchos interrogantes. Y seguro sabes que la estabilidad de dS solutions a nivel cuántico es algo muy peliagudo. En particular, sobre los números de KKLT: Son números que si bien cuadran, están metidos con calzador. Por eso no me gusta. Puede hacerse, desde luego, no le quito crédito o valor. Pero creo que puedo sostener la idea que no me convencen «los números» o el propio approach «construcción» (no digo que no sea posible).
Bueno, me voy a pasar apuntes (aburre pero así este año espero poder no perder tiempo en otros menesteres).
1) «El grupo mencionado en el paper al respecto de gaugear la SUGRA no es el de U dualidad sino el del “primo” electromagnético. »
Esto es falso. En el paper que cite, http://arxiv.org/pdf/hep-th/9605032v1.pdf , se gaugea un subgrupo de U (embebido naturalmente en U), que a su vez se embebe en Sp(2n,R). Esto es exactamente lo que yo dije en la definicion que use. En concreto, el subgrupo de U que se gaugea es el que tiene un embedding block-diagonal en Sp(2n,R). El grupo Sp(2n,R) no es ni siquiera una simetria de la accion ni de las ecuaciones de movimiento de la teoria.
2) Sin comentarios.
3) Problema: Embeber dS en Teoria de Cuerdas. Se hace explicitamente en KKLT, donde por tanto se soluciona tal problema. Otros asuntos relacionados con el problema quedaran por resolver, no lo dudo. Sobre la Cosmologia en Teoria de Cuerdas, ni idea, pero creo que no estan tan lejos de poder dar alguna «prediccion».
El problema de embeber dS en Teoria de Cuerdas no tiene nada que ver con el problema de embeber RS. Es mucho mas facil embeber RS y de hecho sale de forma bastante natural, al contrario de dS.
Te cito:
«Pero al embedding le criticaría la forma de hacerlo»
Que problema hay con el embedding que aparece en KKLT?
Hola.
1) No fue exactamente así como lo dijiste la primera vez (si lees, por favor, lo que pusiste antes de que mis comentarios te hicieran tirar de bibliografía), y lo que yo «entendí» (lee más arriba, quizás mal, no lo sé), era que al gaugear lo hacías con un grupo de dualidad U y lo identificabas con el simpléctico (ya había aludido a ello antes, posiblemente ahí, me equivoqué entendiendo mal lo que estabas tratando de decir). Supongo que de nuevo este tipo de rifi-rafe ocurre por no precisar las definiciones suficientemente (antes de la cita, el lenguaje no era del todo suficientemente claro para mí) desde el principio (nos pasó con la definición de teoría «gauge»). Si lo califiqué de absurdo fue porque no conocía lo del grupo simpléctico (debido a nuestro intercambio de mensajes y el hilo ya sabes algo más sobre lo que puedo conocer, supongo), aunque sí sabía lo del grupo de U dualidad como grupo de simetrías ocultas (tanto discreto como versión continua) de SUGRA/M-theory, y por eso, pienso no te entendí. Ahora que has explicado la frase convenientemente, entiendo perfectamente lo que dices. En ese sentido, creo que entendiendo lo que dices, te concedo la corrección en lo que mencionabas.
2) Lo celebro.
3) Si miras arriba(quizás no lo he dicho suficientemente claro), mi critica respecto a dS no es que no se pueda, sino que observo los siguientes problemas:
i) Estabilidad. No me convencen las cuentas (incluso si acepto la cota del artículo), a parte de que para llegar a ellas hay que hacer asunciones sumamente particulares (me refiero a la cota del tiempo de vida, y eso no garantiza que no haya algo que no hayamos tenido en cuenta que lo vuelva inestable con menor tiempo de vida del universo).
ii) Para deducir la el dS hay que «cocinarse» lo anterior. Es la habitual crítica supongo de que «todo es calculable», pero ¿qué selecciona el dS? ¿Por qué se hace de esa en particular y no otra?¿Sólo porque se puede? Creo que los autores, de peso, lo dejan claro desde el principio. Es una construcción, no una «derivación» limpia. Es una construcción efectiva de la que tengo mis dudas razonables.
iii) No he dicho en ningún momento que sean el mismo problema, pero sí que encontrar ese tipo de soluciones curvas «warped» era un problema (y aún lo es, pero el problema no es ya si existen inmersas entre las soluciones de la teoría sino la forma de seleccionarlas). Corrígeme, si es así, si he dicho o no que sea el mismo problema embeber RS y dS (o incluso AdS) sino que era un problema, hace algún tiempo, lograr «embeber» dichas geometrías o más aún encontrar ese tipo de soluciones (AdS efectivamente con menos problemas) en el vacío de supercuerdas. Y, quitando AdS y los problemas de una teoría de campos sobre ese tipo de espacios, dS es el meollo por Cosmología. Sé que es más «natural» encontrar RS y soluciones tipo AdS en SUGRA. Lo que yo quería decir arriba(lo mismo me expliqué mal), es que para embeber dS o AdS en cuerdas (ó RS) hay que usar formalismos altamente no triviales. dS ó AdS o RS son espacios (altamente) curvados, y en ellos, a nivel cuántico (no hablo aquí sólo de la solución clásica), si queremos tener una teoría cuántica de campos en espacio curvado lleva a considerar procesos de producción de partículas-antipartículas (efecto Hawking). Por supuesto, la crítica a este argumento es que la constante cosmológica observada es muy pequeña, PERO, irónicamente hablando, todas las teorías cuánticas de campos predicen (hasta donde yo sé) una constante cosmológica demasiado grande. Ninguna teoría soluciona esto, aunque tenemos propuestas…
4) Embedding: si has leido hasta aquí, espero que haya aclarado que lo que yo veo «criticable» es que depende de una selección «ad hoc» de las condiciones que lleva a encontrar dicha solución. Como tú mismo has dicho, es «difícil» dS en comparación con AdS, y eso lleva a hacer un montón de hipótesis por las que evidemente, se pasa de puntillas en el propio artículo. Feynman decía algo similar (creo recordar) respecto la forma de enrollar las dimensiones en teoría de cuerdas… Creo que es una crítica razonable. Seleccionar un vacío dS y embeberlo «porque se puede bajo hipótesis A, B, C,…» no me parece elegante ni simple, aparte de que no se responde a las cuestiones fundamentales. Por supuesto, este tipo de argumentos están siempre en ciencia. A nivel algo más técnico, la «cocina» para obtener dS, estarás de acuerdo, es bastante particular.
5) Respecto a lo que comentas antes que no se está tan lejos en Cosmología de cuerdas de «hacer predicciones». El arte de la predicción, como decía gente más lista que yo, es difícil. Las predicciones que hagamos nosotros o lo que nos cuentan de que que «están cerca» no deja de ser algo tremendamente subjetivo. Yo pienso que no es tan simple (siempre puede haber una revolución y alguien que saque un «pelotazo» impresionante) y que aún queda. El problema de la constante cosmológica o la obtención de parámetros cosmológicos desde cuerdas, y es mi opinión, no es en absoluto trivial. Faltan años para eso. Eso si no sale una inteligencia artificial antes que nos robe el trabajo en ese campo. Ya te mencioné que con un ciberamigo (también estudió como tú en la UAM parte del Máster) he apostado que no creo que se pruebe la finitud de SUGRA N=8 a todo loop antes de 2017. Me gusta apostar a «null results».
6) Releyendo con cuidado el hilo, he encontrado algo a lo que no te había contestado. Dije arriba que se prefiere Kähler y no hyperkähler para compactificar. NO dije, creo, en ningún momento, que hyperkähler no fuera una variedad kähler. La distinción técnica (a nivel local) de todas las variedades complejas o de las de tipo Kähler no era algo que me preocupara excesivamente porque no sabía con quien estaba hablando, pero sí quise destacar, que se prefiere Kähler a hyperkähler (toda variedad hyperkähler es Kähler, pero hay variedades Kähler no hyperkähler, y como bien dices hay variedades cuaterniónicas de tipo Kähler, pero NO era eso lo que quería destacar ni me quería meter ahí, sino que las construcciones que se hacen es, generalmente sobre variedades peculiares, de tipo Kähler, no necesariamente hyperkähler-creo que ahí sí que lo expresé bien, acabo de releerlo para no meter la pata, pues yo dije «Normalemente se prefiere Kähler no hyperkähler para compactificar» , aunque sé que hay algunas compactificaciones sobre estas últimas).
No quería entrar demasiado en este punto como en la elección del tipo de geometría (o la selección de sus propiedades) para compactificar. La razón es que en la literatura en ocasiones se habla de «geometría Kähler especial» cuando los físicos hablamos de escalares en supergravedad, o bien los matemáticos habláis de geometría o variedades hyperkähler cuando en ocasiones se las puede llamar también «variedades afines cuaterniónicas Kähler». De hecho, ya que eres de ese campo, las variedades hyper-kähler (corrígeme si me equivoco) pueden ser vistas como un subcaso de «variededades cuaterniónicas Kähler» con «curvatura SU(2) nula». Déjame destacarte que en algunos casos y estudios específicos (tanto de artículos, libros, etc), los estudios de supergravedad «asumen» o se restringen a variedades de este tipo, cuaterniónicas Kähler CON curvatura escalar negativa (por interés, claro), ya que se «asume» (de nuevo es una asunción) que este tipo de espacios son los únicos que se dan como solución en SUGRA con energía positiva PARA TODOS los campos. Esto viene así contado en otro libro de SUGRA, que te puedo citar si lo deseas (supergravedad, de Freedman y Van Proeyen, página 441, notas a pie de esa misma página.). No me invento estas cosas (están en ese libro), como no me suelo inventar mis argumentos o mis «referencias» en general (otra cosa es que pueda equivocarme de referencia o acertar más o menos el artículos donde se encuentra cierta idea), aunque admito que en ocasiones me explico fatal queriendo ser más intuitivo o explicarlo con mis palabras (por eso siempre digo que las definiciones matemáticas son sutiles y hay que matizarlas si entramos en una discusión con un experto, y esto a priori es un foro de divulgación científica, no un lugar para una discusión académica avanzada de algo como la geometría compleja, la geometría compleja especial o las geometrías excepcionales porque uno no espera encontrar -ni puede adivinar desde el principio- si con quien discute sabe lo que dice o no -de ahí mis tests- para precisar lo que digo en lugar de «fugar ideas»). Pero tienes toda la razón del mundo, al nivel al que iba la charla, y te aseguro que yo me autoimpongo mucho generalmente aquí (aunque me dé caprichos y me ponga a sacar mi verborrea o fuga de ideas usual virtual) para no ser demasiado ininteligible, no importaba esa cuestión técnica, aunque quería dejar este asunto también resuelto. ¿Lo está?
Un saludo.
Bueno, después de leer el post y los comentarios, sólo se me ocurre decir una cosa: éste tipo de espectáculos ni en el circo de Charlie Rivel.
Me estoy leyendo el review de Douglas y Kachru, «Flux compactification», y es gracioso como aluden a la compactificacion de Kaluza-Klein clasica. Al menos aluden, que algo es algo. Citan la misma coleccion de articulos a la que he aludido más arriba, el libraco de Appelquist et al (1987), pero colocan el resto del trabajo en un tiempo indefinido «After it was realized that Nature employs non-Abelian gauge fields» que hace pensar que es cosa de los años cincuenta o sesenta. Remarcan que «One can even find seven-dimensional manifolds for which this is the standard model group», pero no antes de haber desmotivado diciendo que estas teorias de KK son «too simple to be quasirealistic»; y ponen un ejemplo que llaman de Freund-Rubin pero en dimension seis y sin citar el caso general ni el de dimension once, con lo que se pierde el detalle de que en D=11 sugra con FR la compactificacion que se estabiliza es la 7+4.
Para colmo, segun el registro bibliotecario el Applequist et al solo esta en tres bibliotecas publicas, dos en Barcelona y una en el Pais Vasco. Supongo que eso sera porque muchas bibliotecas de departamento no estan indexadas, pero dificulta bastante el enterarse de qué va lo de Kaluza-Klein.
Y estaba pensando, ¿seguro que queremos una solucion deSitter? ¿no seguimos teniendo entonces el problema de la energia del vacio electrodebil?
Parece que seria mas logico pedir un espacio-tiempo anti-deSitter de unos 246 GeV, de forma que se compensara exactamente con el vacio del higgs y nos diera esas decimas de electronvoltio que hacen falta. ¿no?
“Pero dificulta bastante el enterarse de qué va lo de Kaluza-Klein”.
Bueno, el tema es complejo. Resulta que Oskar Klein llegó a la misma conclusión que Yang y Mills, sólo que lo hizo dos décadas antes. Pero en el fragor de la segunda guerra mundial la solución de Klein pasó desapercibida.
“Remarcan que ““One can even find seven-dimensional manifolds for which this is the standard model group”, pero no antes de haber desmotivado diciendo que estas teorias de KK son “too simple to be quasirealistic””.
Según Lee Smolin, el problema es el siguiente. El modelo de Kaluza-Klein establece que la dimensión extra o adicional está enroscada o compactificada de tal modo que forma un círculo cuyo radio está congelado, no se modifica en el espacio y en el tiempo. La congelación citada es un obús a la línea de flotación de la RG cuya geometría es dinámica. A esto había que añadirle los problemas derivados de algunas inconsistencias halladas en la simetría CPT.
Artemio. NO hay inconsistencia en la simetría CPT. CPT es resultado del matrimonio de relatividad y mecánica cuántica. En general, y con algunos casos excepcionales que habría que mencionar, cualquier teoría local relativista (invariante Lorent, o incluso invariante por el grupo de Poincaré) de campos cuánticos es CPT invariante. El recíproco también es cierto en general, y cualquier teoría que sea CPT invariante es (en general) invariante Lorentz.
Si lo que querías decir es que las simetrías C, P, T, o CP, CT,PT están rotas. Es cierto sí, pero por la interacción débil o electrodébil.
La extensión del modelo estándar dada por la SME (Standard Model Extension) es un framework que parametriza todas las posibles violaciones de CPT y de la invarianza Lorentz, así como sus diferentes opciones. Hasta la fecha, muy poco es conocido sobre los parámetros de SME, pero los resultados son compatibles con la invarianza Lorentz y CPT. También, los distintos experimentos y mediciones astrofísicas dan fuertes ligaduras a posibles deformaciones en las relaciones de dispersión de la relatividad especial, a saber $latex E(p,m)=E^2+p^2$ sigue siendo válido tanto en el Tevatron, como el LHC como en toda medida astrofísica.
La única salvedad, si queréis verlo así, es materia oscura y energía oscura…No tenemos ni idea sobre qué son ni sus propiedades…
“Si lo que querías decir es que las simetrías”…
Yo no quiero decir nada, sólo transcribo la opinión de Lee Smolin.
“La única salvedad, si queréis verlo así, es materia oscura y energía oscura…No tenemos ni idea sobre qué son ni sus propiedades”…
Bueno, ideas sí hay, otra cosa es que sean consistentes.
Queremos de Sitter, Alejandro, porque Cosmología «dice» que el Universo es de Sitter, o al menos eso dice el modelo de concordancia LCDM. Más allá de cosas que no sé cómo tomarme, como la que ha salido hoy de los cerebros de Boltzmann (Carroll et al.), y que es polémico, el que prefiramos de Sitter es simple petición cosmológica. Y ahora WMAP no está solo, PLANCK lo ha confirmado (excepción echa de unos pequeños cambios leves en los porcentajes de energía y materia oscura).
Retrospectivamente hablando, SUSY antes era «feliz» (pre 1998) porque el universo parecía «plano» y esperábamos deceleración y no aceleración positiva por la gravedad. SUSY era «guay» porque es una simetría que permite explicar que la constante cosmológica sea cero. La naturaleza se ha mostrado perversa y nos dice «aceleración positiva» (a no ser que prefieras otras cosas más exóticas propuestas como que el tiempo cósmico no transcurre de forma uniforme, como algunos han propuesto). Por tanto, si el universo es de Sitter, hay que obtener de Sitter. Yo pienso que una relatividad cinemática en espacios de Sitter y su dinámica asociada, pobremente comprendida, así como su teoría de campos debe desarrollarse más porque, hasta ahora, asumimos que la constante cosmológica es la energía del vacío EN un espacio plano de Minkovski en la teoría cuántica de campos. El problema de la constante cosmológica, que antes de 1998 (cuando se pensaba que era nula) era argumento teórico en favor de supersimetría, se ha vuelto en su contra. El Universo parece que está acelerado positviamente a muy grandes escalas, y eso lleva a una constante cosmológica canija NO nula. El valor cero no parece «compatible» con las observaciones. SUSY sabemos que está rota a cierta escala de energía X. El problema ahora es ¿puede alguien generar una energía del vacío como la observada desde un modelo supersimétrico? Cualquier construcción conocida genera, si rompemos SUSY, una constante cosmológica que está fuera de control. Es «la venganza de $latex Lambda$». Mi impresión es que el problema está en que calculamos todo en Minkovski spacetime. Habría que construir una QFT en dS spacetime y su «relatividad» cinemática asociada, en la que dicha constante no sufriera correcciones. Desconozco cómo hacerlo, de otra forma, ya habría hablado con alguien (aunque es «work in progress»).
En síntesis:
i) Pre 1998: Problema de la constante cosmológica y SUSY. SUSY esgrimida como principio de simetría por el que la constante cosmológica, energía del vacío o «energía oscura», término de presión en las ecuaciones de Einstein, se anulaba. Teóricos SUSY felices y felicísimos porque se solucionaba el problema, exepción hecha de encontrar evidencias experimentales de SUSY a energías suficientemente bajas.
ii) 1998. Descubrimiento de la expansión positivamente acelerada del universo a grandes escalas. Renacer del término cosmológico de sus «cenizas» (esto habría asombrado a Einstein seguro, a parte de que le hubiera dado el Nobel ¿?).
iii) Post 1998. Diferentes experimentos confirman las observaciones. SUSY que era feliz, ahora se enfrenta a la venganza de $latex Lambda$. Si la constante cosmológica no es cero, y tiene el valor que tiene, SUSY está en apuros. Alguien podría argumentar que tal vez este problema ya estaba antes, porque el Modelo Estándar no es supersimétrico (no hay match entre el número de bosones y fermiones) y que el problema estaba latente ahí, pero si uno lee la bibliografía, se solía repetir como mantra que supersimetría podría ser la solución a la cancelación de la constante a una energía. Lo que evidentemente no se decía, y ahora tenemos encima el valor de $latex Lambda$, es que supersimetría si existe «vive» a una energía «alta», y hay que romper susy. La diferencia es que si bien antes había que encontrar una forma de romper susy que NO produjera una energía del vacío, y había que cuidar de la cancelación a la misma de fermiones y bosones, ahora ese escenario ha cambiado. Ahora hay que romper SUSY dando una constante cosmológica NO nula y que encima es entre 60 y 123 órdenes de magnitud más pequeña experimentalmente que cualquier predicción teórica de todo modelo supersimétrico a disposición. Es que, el problema es gordo…A nivel teórico, es análogo al de la catástrofe ultravioleta del cuerpo negro en el siglo XIX…
Lo que quiero decir es, «¿Seguro que queremos una solucion deSitter ya antes de sumar la contribucion de la ruptura espontanea de simetria?» Parece que lo que en realidad debieramos buscar es una solucion AdS lo suficientemente negativa para que luego al sumar esa contribución nos diera la observada.
La contribución a la energía del vacío de fermiones y bosones tiene signo opuesto vía diagramas de Feynman. No veo cómo el que busquemos una solución cosmológica con constante cosmológica negativa para que luego al añadir las contribuciones de fermiones y bosones dé la energía del vacío observada es mejor que buscar directamente de Sitter. En ambos casos hay que eliminar los mismos órdenes de magnitud con «fine tuning». Eso de que observemos de Sitter pero el Universo sea secretamente anti de Sitter lo veo bastante bizarro. Eso sí,…Transiciones entre Anti-De Sitter y de Sitter ¿son posibles? También sabemos que la energía oscura (sea lo que sea) no ha dominado siempre la expansión: fue hace unos miles de millones de años cuando empezó a dominar y posiblemente dominó durante la inflación (si nos creemos ésta).
NO sé, o no te explicas bien, o no entiendo lo suficiente tu idea Alejandro.
Las correcciones al Higgs tienen signo opuesto. La energia del vacio del Higgs ahi esta, como quien dice para quedarse. Lo que no sé es como se salta de una energia del vacio electrodebil a una contribucion a la densidad de energia, pero bueno, lo que siempre se ha dicho es que la energia del vacio de teoria de campos estaba en total contradiccion con la cte cosmologia observada, asi que me creo que se puede saltar de un concepto al otro.
El caso es que con tanto rollo de los KKLT me he descargado algunos de los papers para empezar a leer y bueno, cuando te presentan el «uplifting» ya para empezar no se queda uno convencido de si han compactificado en dS o han compactificado en AdS y tuneado luego. Ya te dire cuando me los haya leido.
Pero ademas hablaban, en la introduccion de Douglas y Kachru, de la solucion de Freund-Rubin haciendo enfasis de que tiene el problema de que el espacio compacto y el espacio AdS que producen deben tener curvaturas del mismo orden de magnitud para que sea estable. Y me he preguntado si eso no es más bien una feature que un bug, porque si por un lado el AdS te mete una cte cosmologica negativa y por otro lado el espacio compacto te mete una ruptura de simetria que te crea una vacio cuantico cuya energia tambien es del orden del radio de ese espacio compacto, entonces ahi tenemos una contribucion positiva a la cte cosmologica, que cancela aproximadamente la negativa justo por la condicion de estabilidad de la compactificacion, sin ningun fine tunning por enmedio.
Aunque parezca sorprendente, la hipotetizada y futura fusión de la Vía y Andrómeda halla difícil acomodo en el modelo expansivo del cosmos. ¿Por qué dos galaxias, en vez de expandirse cada una por su lado, corren a fusionarse? Al menos una de las dos no acelera sino que desacelera, las dos galaxias crean una singularidad en el marco de un universo que expansiona. En una perspectiva uni, bi y tridimensional se está creando una región del cosmos que no es expansiva, más bien al contrario. Ahora bien, ¿podemos decir lo mismo desde una perspectiva 5D, kaluziana?
Artemio, el canibalismo galáctico y las colisiones (y fusión) entre galaxias son fenómenos habituales en el universo y no tienen nada que ver con la expansión cósmica (ya que se trata de un fenómeno local en los halos galácticos, los cúmulos galácticos y la web cósmica). Como la gravedad es atractiva las cosas cercanas tienden a chocar. Se estima que el 95% de las galaxias con masa similar a la Vía Láctea han sufrido al menos una colisión contra otra galaxia de tamaño similar en los últimos 10.000 millones de años [arxiv:0711.5027].
Francis, gracias por el comentario. Prefiero hablar de fusión en vez de canibalismo, vamos, no me gustaría que un andromedano me canibalice ;-D
“Como la gravedad es atractiva las cosas cercanas tienden a chocar”.
Bueno, sí, pero una cosa es que tiendan a chocar y otra es que lo hagan. De
momento el planeta no choca con el sol, y están muy cerca.
¿Cuál es en tu opinión la definición de un universo que se expande si zonas del mismo tienden a contraerse/fusionarse?
Artemio, no hay zonas del universo que tiendan a contraerse o fusionarse, hay objetos en el universo que se fusionan (como la nube de gas que dio lugar al Sistema Solar y los planetesimales que dieron lugar a los planetas, la formación de galaxias pasa por procesos de fusión que no tienen nada que ver con la expansión del espacio). De hecho el volumen de espacio ocupado por los objetos que hay en el espacio es ridículo. Tendemos a imaginar que la galaxia está «rellena» y que el Sistema Solar está «relleno» y que los átomos de tu cuerpo están «rellenos» pero en realidad están prácticamente vacíos.
Magufos hay por todas partes :). Supongo que es cosa de «Matrix». Este blog y Cuentos Cuánticos los han sufrido. Y los sufren, de vez en cuando. Aunque cierto es que podemos equivocarnos al identificarlos.
Hola amarashiki.
1) La primera definicion que di es perfectamente correcta. En cualquier caso me alegro de haber aclarado este punto.
2) 🙂
3) En KKLT se embebe dS, que es a lo que me referia. Como es normal en un paper de investigacion, deja cuestiones sin resolver y proponer nuevas. En cuanto a tus pegas a KKLT, poco puedo aportar. En efecto, es una construccion ad-hoc para lograr embeber dS, y es una construccion un poco «sucia» o «chapucera», dependiendo de como se vea. No obstante
«No me convencen las cuentas (incluso si acepto la cota del artículo)…»
El articulo KKLT es un articulo muy complejo tecnicamente, y para cuestionar asi las cuentas que se hacen hay que estar muy seguro de lo que se dice, y por supuesto, haberselas hecho…Yo personalmente no lo he hecho.
4) Sin comentarios, y parcialmente de acuerdo.
5) Sin comentarios, poco puedo aportar.
6) » NO dije, creo, en ningún momento, que hyperkähler no fuera una variedad kähler.»
No, pero parecias implicarlo, ya que la expresion que usaste (se prefiere A sobre B) se suele usar para categorias «disjuntas».
«sino que las construcciones que se hacen es, generalmente sobre variedades peculiares, de tipo Kähler, no necesariamente hyperkähler-creo que ahí sí que lo expresé bien»
A que construcciones te refieres?
«pues yo dije “Normalemente se prefiere Kähler no hyperkähler para compactificar” , aunque sé que hay algunas compactificaciones sobre estas últimas»
Yo no conozco ninguna; podrias darme una referencia?
«La razón es que en la literatura en ocasiones se habla de “geometría Kähler especial” cuando los físicos hablamos de escalares en supergravedad»
La geometria especial kahler solo corresponde a los escalares de los vector multiples en N=2. Otras supergravedades tienen otras geometrias escalares.
«Déjame destacarte que en algunos casos y estudios específicos (tanto de artículos, libros, etc), los estudios de supergravedad “asumen” o se restringen a variedades de este tipo, cuaterniónicas Kähler CON curvatura escalar negativa (por interés, claro), ya que se “asume” (de nuevo es una asunción) que este tipo de espacios son los únicos que se dan como solución en SUGRA con energía positiva PARA TODOS los campos.»
Estamos hablando de geometrias escalares, no de soluciones de la teoria de Supergravedad. Tales geometrias vienen impuestas exclusivamente por supersimetria.
Hola, Kac-Moody:
1) Puede, pero no era lo suficientemente fina como para que a mí no indujera a error. Y ya vimos que me exalto si veo algo que me parece erróneo. Estoy contento de haber solucionado este punto (que pienso sigue siendo cuestión única de lenguaje escrito y quizás de una excesiva sobrecarga emocional). :).
2) Perfect!
3) Chapucera quizás es ser demasiado cruel con un paper de casi 2000 citas ¿no? Aunque yo creo que lo esencial ahí son «las asunciones» que hacen. Estoy seguro que Feynman diría algo más rocambolesco que yo, pero yo no me atrevo a decir «chapuzas» ( quizás los fervientes anti-stringers se echan unas risas con el paper, ¿no crees?) si no eres absolutamente anti-strings/anti-branes/anti-etc.
4) y 5) …Mmm…Sí, creo que algo puedes aportar…¿Tienes alguna idea de cómo podemos competir con los chinos y las «inteligencias artificiales científicas» que se aproximan cada vez más en Matemáticas? XD Te lo digo por si has al menos leido por encima el artículo de Post-Human Mathematics que aparecía hoy/ayer en el arxiv…(El de los cerebros de Boltzmann de Carroll ya es demasiado para mi mente hoy, le leeré con cuidado otro día…)
6) Parte A) Sobre las construcciones a las que me refiero, es a las compactificaciones en las que la variedad es una Calabi-Yau, variedad compleja Kahler. ¿Estoy en lo cierto? Retomando el hilo con lo que mencioné, en los 80 el entusiasmo de Witten por las Calabi-Yau (se dice que el propio Witten llamó por teléfono a Yau) era que la idea era poder seleccionar (supongo) de las Calabi-Yau una que correspondiera a nuestro Universo. HOy sabemos, que hay demasiadas Calabi-Yau y que muchas de ellas ( no totalmente enumeradas, me refiero, a las Calabi-Yau) pueden en principio reproducir las propiedades del mismo ( hablo en el contexto del problema del landscape, que está relacionado con este problema y los posibles vacíos de la teoría de supercuerdas/teoría M).
Parte B) Te puedo citar al menos alguna de las que tengo más a mano, sin archivar en disco duro todavía (estoy esperando a acabar los apuntes para hacer un backup de las descargas tanto de verano y de los útlimos meses, como de mis fotos y documentos propios de este año). Te puedo citar las siguientes:
arxiv.org/pdf/hep-th/0612023 The moduli space of hyper-Kahler four-fold compactifications
Más reciente es ésta
http://arxiv.org/abs/1206.2349 Black Holes and Fourfolds
De hecho ésta me la descargué hace unos meses porque contiene un sucinto apéndice que sirve para «recordar» algunas generalidades de la geometría de esas variedades hyperkähler (no me interesan esas geometrías tanto como años atrás, ya no soy «joven» supongo). Y aunque no me gusta meterme en esas cosas, siempre viene bien a mano tener algún paper con algún apéndice que te resume algún tópico matemático relevante en geometría de forma breve.
De las matizaciones que haces, poco puedo añadir, salvo que de nuevo se hacen asunciones que a mí, personalmente (como la supersimetría), aunque me parecían y aún me parecen fascinantes, las estoy perdiendo el gusto poco a poco. No digo que no pueda ser, simplemente, que en el mundo matemático está muy bien hacer hipótesis para estudiar objetos, pero el mundo físico tiene otra forma más de operar.
NOTA: Sin pruebas de existencia de supersimetría, estamos jodidos… Y todo este aparejo será bonito y tal, pero no sería más que un ejercicio de matemáticas. La idea es aplicarlo a algo físico al final, como físico que soy digo…XD.
Bueno, la fantasía está bien, pero hay que relajar las definiciones de vez en cuando para salir de un sistema restrictivo. A mí me gusta preguntarme cosas del tipo ¿y si cambiamos esta idea por esta otra?¿Podría funcionar esta teoría si hago esto o aquello? Matemáticamente hablando, claro, es más sutil, y las definiciones e incluso los postulados físicos y matemáticos que haces (tu conjunto de «axiomas», vaya) te selecciona o impone cosas. Me gusta estar en la frontera de «las normas» y cambiarlas si puedo.
1) Era perfectamente fina y correcta.
2) OK.
3) No soy ni anti ni pro strings.
4), 5) No tengo nada que aportar, mis conocimientos de Cosmologia son muy escasos, nunca me ha interesado el tema. Y no se por que hay que competir contra los chinos…
6) Gracias por las referencias.
«A mí me gusta preguntarme cosas del tipo ¿y si cambiamos esta idea por esta otra?¿Podría funcionar esta teoría si hago esto o aquello?. Me gusta estar en la frontera de “las normas” y cambiarlas si puedo.»
Eso es lo que hacen todos los Fisicos….
Alejandro, te daré mi subjetiva opinión. Para abordar un modelo de unificación prefiero estudiar los átomos y partículas, las fuerzas y la energía antes de hurgar en la matemática, la geometría y la topología. Aun a riesgo de equivocarme, entiendo que hay suficientes modelos topológicos a disposición de los físicos para encajarlos en sus pesquisas. Por muy sofisticado que sea un diseño matemático-topológico, poco nos dirá si a) los datos físicos son incorrectos, b) si ciertos experimentos se declaran anatema, y c) si ciertas ideas pasan desapercibidas por el influjo del mainstream y las inevitables capillitas.
Bueno, si se trata de estudiar relaciones «desde abajo», de nuevo te envio tres posts mas atras, al de mi «guest post», donde hay unas cuantas. Y nada mainstream. Hasta luego.
Alejandro, me quedó un apunte en el tintero. Ayer leía el libro de un cuerdista y entendí a la perfección una de las críticas formulada a esa teoría. Desde el punto de vista de un físico teórico y experimental lo que vale es el espacio que se pretende estudiar. Por ejemplo, si para explicar lo que son las cuerdas las ponemos a vibrar en la superficie de un tablero, que es un “espacio” de dos dimensiones, no obtenemos el mismo resultado que si las ponemos a vibrar en el núcleo del sol, en el vacío interestelar o en la singularidad de un agujero negro. Del mismo modo que no podemos levantar un mapa en el aire de la mañana, necesitamos un papel de dos dimensiones, poner a vibrar cuerdas y branas sin tener en cuenta el espacio que las contiene me parece raro.
Francis, entonces debo entender que el universo no se expande. Sin embargo hay galaxias remotas que se alejan de nosotros a velocidad taquiónica.
“Hay objetos en el universo que se fusionan (como la nube de gas que dio lugar al Sistema Solar)”…
Hum…, este supuesto no es el mismo que la hipotetizada fusión de la Vía y Andrómeda, al menos que yo sepa.
“La formación de galaxias pasa por procesos de fusión que no tienen nada que ver con la expansión del espacio”…
A ver si lo entiendo. Se cree que lo que se estira es el tejido universal arrastrando con él a las galaxias y cúmulos galácticos. Ahora bien, la contracción/fusión de las galaxias ralentiza el estiramiento de aquellas regiones donde se producen las fusiones de las galaxias.
Pero donde hay un plegamiento infinito o cuasi-infinito es en las zonas donde hay agujeros negros. En este supuesto no hay estiramiento sino simple ruptura o colapso de la materia. En cualquier caso, agradezco tu respuesta.
Artemio, yo no he dicho eso. La expansión del universo es un fenómeno global, no local. Los comportamientos locales son independientes de los globales.
Hay preciosas imágenes de galaxias en colisión, como ésta:

Pensando en eso de los moduli… ¿Os habeis fijado que si solo tuvieramos las componentes del graviton, la compactificacion a la esfera no funcionaria para D>8? Esto es, por un lado el graviton tiene D(D-3)/2 componentes, por otro un espacio de d=D-4 dimensiones admite d(d+1)/2 isometrias como maximo, que es el caso de la esfera, y por lo tanto d(d+1)/2 bosones del grupo gauge y d(d+1) componentes. Sustituyento esto es (D-4)(D-3) y restando vemos que el numero de componentes que sobran es (D-3)(8-D)/2.
Se me hace raro porque pensaba que el procedimiento de Kaluza Klein se podia aplicar sobre cualquier esfera en cualquier numero de dimensiones. ¿Me he equivocado en la resta, o falla la intuicion de que los campos gauge salen de la metrica y por tanto del graviton?
De hecho entre las componentes que sobran hay que reservar dos para el graviton 4D, asi que D=8 tambien falla la cuenta.
Una compactificacion no funciona cuando el espacio compacto no es compatible con las ecuaciones de movimiento.
Alejandro, soy incapaz de responder a tus preguntas ;-D
Lo que pregunto es lo siguiente, ¿si el gravitón es una partícula escalar hemos de concluir que su métrica tendría que ser consistente respecto del espacio contenido en cualquier esfera de cualquier dimensión? Si la respuesta es afirmativa se cumple la dinamicidad de la RG; si la respuesta es negativa, la métrica colapsa en una singularidad.
“Se me hace raro porque pensaba que el procedimiento de Kaluza Klein se podía aplicar sobre cualquier esfera en cualquier número de dimensiones”.
El problema del modelo de Kaluza-Klein está en que el radio del círculo diminuto que describe a la dimensión extra está congelado. Pero tengo entendido que los primeros cuerdistas salvaron esta dificultad al añadir varias dimensiones más, aunque desconozco por completo el formalismo matemático usado para llegar a esa conclusión.
Tengo un par de ideas sobre la unificación, pero lejos de hurgar en las teorías modernas me dispongo a leer un libro de J.C. Maxwell, “Materia y movimiento”, por fortuna traducido al español. La obra se publicó en 1876 😉
Artemio yo tengo una pregunta para ti, ahí va: Cuando escribes un comentario en este blog ¿realmente entiendes algo de lo escribes? No te lo tomes a mal pero parece como si cogieras al azar palabras relacionadas con la Física y las mezclases de forma inconexa para crear frases sin sentido. Te lo digo sin acritud…
Por eso planteo mis preguntas en voz alta, pero tu respuesta me deja in albis…, sin acritud ¿eh?
Artemio, la pregunta (estimo) iria por lo siguiente:
«¿si el gravitón es una partícula escalar hemos de concluir que su métrica tendría que ser consistente respecto del espacio contenido en cualquier esfera de cualquier dimensión?»
¿Esta bien esto? Hasta donde mis limitados conocimientos llegan, la metrica es una funcion distancia aplicada a un conjunto de puntos, es decir, se define en un espacio, no se que seria la metrica de una particula. Ademas, el hipotetico graviton no seria una «particula escalar» (nota: escalar es el campo hasta donde se), ya que tendria spin. Quizas puedas aclararte mejor.
Artemio dice: «¿si el gravitón es una partícula escalar…?» En la teoría de Newton, el «gravitón» sería una partícula escalar (espín cero); en la teoría de Einstein, el gravitón es una partícula de espín 2 y hay evidencia experimental desde hace casi un siglo de que la teoría de Newton no es correcta; además, hay evidencia experimental de que la gravedad es un campo tensorial (la última de Gravity Probe B de la NASA fue noticia hace poco).
Artemio dice: «El problema del modelo de Kaluza-Klein está en que el radio del círculo diminuto que describe a la dimensión extra está congelado.» La palabra «congelado» no tiene sentido en este contexto; supongo que quieres decir que es una constante fijada por la compactificación a mano (ad hoc o por principio antrópico). En cualquier teoría tipo supergravedad o tipo supercuerdas, este tipo de parámetros (llamados módulos, o moduli en inglés) son dinámicos y corresponden a campos escalares (su valor constante es el valor en el vacío de dicho campo).
«….salvaron esta dificultad…» Supongo que te refieres a la necesidad de usar un argumento ad hoc o el principio antrópico para fijar el valor constante. «… al añadir varias dimensiones más…» no es cierto, ya que el problema se mantiene incluso en dicho caso; para salvar la dificultad hay que considerar que la compactificación es un mecanismo dinámico y que que los moduli son campos.
Disfruta del libro «de J.C. Maxwell, “Materia y movimiento.”
¡Gracias francis por la aclaracion! Por cierto, gran discusion se armo mas arriba, entendi solo las preposiciones. Que si SUGRA, que gaugear, que hiper-kahler, que compactificar, creo que entendi menos que si me hablaran en arameo, jajajaja. Saludos.
Jorge, disculpa mi imprecisión. Mi comentario surge por las preguntas de Alejandro, lo que quiero decir es lo siguiente. Si la gravedad es una ley universal tiene que influir en el plano macro y en el micro, en el átomo y en las galaxias más masivas. Por eso es importante establecer con claridad el espacio que se pretende estudiar, si configuramos el espacio como un conjunto de esferas de cualquier tamaño y en diversas dimensiones, se tiene que cumplir la acción de la gravedad, es decir, se tiene que respetar el dinamismo geométrico de la RG. Si no es así, algo falla, pero como la gravedad no puede fallar porque es una ley universal el problema está en la métrica.
Francis, gracias por tus observaciones, pero algunos de mis argumentos no son tales, sino la transcripción de las opiniones de Lee Smolin, las cuales comparto. Por cierto, que alguno me explique como pueden las cuerdas agitar/vibrar a los fotones, que son partículas sin masa. ¿Cómo puede vibrar algo que no tiene masa?
El libro de Maxwell es una gozada, así como las notas introductorias de J.M. Sánchez Ron.
OK, queda claro. Gracias por la respuesta.
Artemio, en cualquier curso de cuerdas explican qué es el fotón, o cualquier otra partícula, entendida como representaciones del grupo pequeño del Lorentz group (realmente del Poincaré, pero no quiero entras en detalles). Así como el gravitón es un operador con dos índices simétrico (asimilable a una métrica), el fotón lo es de un tensor u operador con un índice (más precisamente una 1-forma). Eso no quita el defecto fundamental de la teoría de cuerdas: explica en principio el origen de a priori un campo con cualquier simetría o número de índices PERO no dice nada en principio, al menos en el estado actual de la teoría, sobre POR QUÉ la masa del electrón o los bosones W y Z vale lo que vale. Y sin embargo, puedes hacer model building con la teoría y «deducir» el Standard Model. Problema: el landscape. Hay en principios un número inconmensurable/enorme de vacíos en dimensiones superiores que permiten deducir el SM+General Relativity en 4D. En los ochenta, la esperanza de Witten y otros muchos, era que se seleccionara alguna variedad de compactificación concreta, tipo Calabi-Yau, que correspondiera al vacío observado. No sólo no es así, sino que hay muchas opciones, demasiadas… Incluso pese al hecho empírico de que vivimos en un (aparentemente) dS space, pese al «logro» de M-theory que unifica todas las supercuerdas y a nivel efectivo en 11d es maximal SUGRA, no sabemos cuantizar una mísera membrana (2-brane) y la revolución de dualidades ha difuminado lo que es gravedad y una teoría QFT pura.
Acabo de tropezarme, en las lecciones de Felix Klein, con una referencia a la «Funcion de Routh» y a la «teoria puramente cinetica» que describieron J. J. Thomson (1888, y articulos en 1886-87) y W. Thomson (1884, «Steps towards a kinetic theory of matter») y se dan un aire, al menos filosoficamente, a las teorias de Kaluza-Klein: crean el campo potencial (la energia potencial) mediante dimensiones extra. Parece ser que la idea sobrevivio hasta en un tratado postumo de Hertz en 1904.
Alejandro, gracias por la referencia. Al hilo de tu nota me gustaría comentar lo siguiente; tanto los físicos terrestres como los astronómicos vieron en la inercia el modo de desmontar el universo finito pero eterno propuesto por Aristóteles, el cosmos aristótelico es infinito en el tiempo (eterno) y finito en el espacio, por fuera de él no había nada. Para justificar la infinitud temporal de su modelo, Aristóteles razonaba que el universo tiene mecanismos de regeneración y autoconsistencia que aseguraban su estabilidad. Es un cosmos “natural” donde objetos y partículas obedecen a la gravedad y al movimiento natural: las piedras caen hacia abajo y el fuego se mueve hacia arriba, es una visión mecanicista del cosmos que llegó a los escolásticos medievales, Copernico y Kepler. Al menos que yo sepa, el elenco atomista fue de los pocos en rivalizar con la propuesta del Estagirita al proponer un modelo universal infinitista donde la infinitud no sólo es temporal sino también espacial.
Por cierto, Alejandro, este asunto tiene tela. De algún modo el modelo del big bang recuerda a la teoría cosmológica aristotélica, desde el momento que hay un bang, grande o pequeño, hay un comienzo para el universo, esto certifica que el universo es finito pues surgió como tal universo en un punto o singularidad del espacio tiempo. El modelo inflacionario, que es expansivo, es un modo de salvar la estaticidad que supone un universo finito cuyo origen se data hace 14.000 millones de años luz. El Estagirita no pondría objeciones puesto que el universo conocido u observable es el único posible pese a que tiene un comienzo, pero aquí se produce una inversión respecto de la perspectiva aristótelica: el universo ya no es infinito en el tiempo, y por tanto no es eterno, pero sí puede ser infinito en el espacio si la energía inicial de la gran explosión confiere inercia y gravedad suficiente para asegurar su estabilidad. El modelo expansivo salva el límite finitista cósmico de la teoría aristótelica pero tiene que encontrar un mecanismo consistente que explique de qué modo el universo es capaz de neutralizar la entropía que lo recorre, es decir, tiene que hallar el modo teórico mediante el cual el universo garantiza su eternidad espacial. Según la propuesta del big bang la eternidad en el tiempo no existe, el universo nació en una fecha medida en años luz, pero no sabemos si antes de la gran explosión había algo. Aristóteles daría saltos de alegría al ver que la inflación confirma la homogeneidad y la isotropía del universo observable, de hecho el filósofo era un enemigo acérrimo de los universos múltiples y de la posibilidad de que hubiese un cosmos anterior al observado hasta la fecha. La naturalidad y la simplicidad de la visión cósmica aristotélica llega hasta nuestros días, aunque parece en retirada, no sólo por el desarrollo de la técnica y la multiplicidad de propuestas teóricas, sino por los rasgos psicológicos visibles en profesionales y profanos que conduce a posar una mirada sobre la naturaleza menos pasiva que en la antigüedad.
Siempre es interesante el analisar todos los posibles caminos en el que un fenómeno puede ser explicable, no soy un experto en el tema, pero creo que cuando se entienda totalmente el boson de higgs, habrá de simplificar significativamente algunos de estos caminos. Es tanto lo que no entendemos y tan poco lo que creemos entender.