Cuando decidí iniciar la aventura de este blog me impuse el buen propósito de no hablar en este blog de los temas en los que investigo de forma profesional. No quería aburrir a los potenciales lectores con innumerables detalles técnicos que no puedo quitarme de la cabeza y que sólo tienen interés para los pocos que nos dedicamos a estas cuestiones. Aún así, de vez en cuando se me ve el plumero.
En el año 2000 propuse como proyecto de investigación el estudio numérico y analítico del zoo de soluciones de la ecuación de Kadomtsev-Petviashvili (KP), con énfasis en las interacciones de múltiples solitones línea, como las que veis en la figura que abre esta entrada. En lugar de considerar su aplicación en el contexto de ondas en aguas someras, como en las fotos de arriba, mi interés se centraba entonces en matrices de líneas de transmisión no lineales. Intuía que la ecuación KP iba a ser ampliamente estudiada durante la primera década del s. XXI. Me ha alegrado ver hoy un artículo de revisión sobre este tema (el zoo de la KP) del genial Yuji Kodama, «KP solitons in shallow water,» ArXiv, 26 Apr 2010 (50 páginas de matemáticas profusamente ilustradas).
 La ecuación KP es una ecuación en derivadas parciales en 2+1 dimensiones que es integrable, es decir, se puede escribir la solución más general posible de su problema de valores iniciales o problema de Cauchy. Es una de las pocas ecuaciones en 2+1 dimensiones que se sabe que es integrable. Su solución general tiene dos partes separadas, una de ellas representa un conjunto de solitones y se escribe mediante el determinate de una matriz, la otra representa términos de radiación de pequeña amplitud y se escribe como una integral de Fourier. El artículo de Kodama revisa una técnica diagramática para representar el primer término, las soluciones multisolitónicas utilizando grafos (Kodama les llama diagramas cordales). Estos grafos recuerdan a los diagramas de Feynman y ayudan a la construcción matemática de estas soluciones, así como a la intepretación de sus propiedades. La figura de la izquierda os muestra la representación diagramática de una solución con un único solitón línea. Kodama presenta las reglas de construcción de los diagramas que representan soluciones con múltiples solitones línea.
La ecuación KP es una ecuación en derivadas parciales en 2+1 dimensiones que es integrable, es decir, se puede escribir la solución más general posible de su problema de valores iniciales o problema de Cauchy. Es una de las pocas ecuaciones en 2+1 dimensiones que se sabe que es integrable. Su solución general tiene dos partes separadas, una de ellas representa un conjunto de solitones y se escribe mediante el determinate de una matriz, la otra representa términos de radiación de pequeña amplitud y se escribe como una integral de Fourier. El artículo de Kodama revisa una técnica diagramática para representar el primer término, las soluciones multisolitónicas utilizando grafos (Kodama les llama diagramas cordales). Estos grafos recuerdan a los diagramas de Feynman y ayudan a la construcción matemática de estas soluciones, así como a la intepretación de sus propiedades. La figura de la izquierda os muestra la representación diagramática de una solución con un único solitón línea. Kodama presenta las reglas de construcción de los diagramas que representan soluciones con múltiples solitones línea.
Abajo tenéis la representación de una solución en la que tres solitones línea colisionan y colapsan para formar un único solitón línea. Con un poco de imaginación podéis ver la película de los hechos. Se ve claro que el solitón línea [1,2] se mueve hacia la izquierda y arriba. Los solitones [1,4] y [3,4] también se mueven hacia la izquierda. Sólo el solitón [2,3] se mueve hacia la derecha. Por eso la solución se denomina 3+1. En t=-8 y t=8 se obervan dos interacciones dobles y en t=0 hay una interacción cuádruple. Hay muchas maneras de imaginarse esta solución. Por ejemplo, los solitones [1,2], [1,4] y [3,4] representan una interacción (vértice) triple que se mueve hacia la izquierda mientras interactúa con un solitón [2,3] que se mueve hacia la derecha. En t=-8 dicho solitón interactúa sólo con el brazo izquierdo y en t=8 sólo con el derecho, en ambos casos introduciendo un desfase que produce un ángulo respecto al vértice triple. No sé si me explico bien… Este tipo de interacción se llama interacción 3+1.
Se pueden representar todo tipo de interacciones múltiples entre solitones línea. Por ejemplo, aquí abajo tenéis la interacción entre 6 solitones líneas, interacción 3+3 (entre dos vértices triples). En este caso hay que tener mucha más imaginación para ver la película de la interacción a partir de tres fotogramas solamente, dada la multiplicidad de interacciones intermedias entre los solitones que muestran las imágenes. La ventaja de la formulación matemática (en este caso del diagrama cordal) es que permite entender fácilmente este tipo de interacciones múltiples entre solitones que aparentan gran complejidad.
Los diagramas cordales (como pasa con los diagramas de Feynman) permiten clasificar todas las posibles soluciones con solitones línea en interacción. Podemos entender las estructuras básicas con las que se forman todas las interacciones posibles, como la soluciones patrón en X o en T (no entraré en detalles). ¿Todas estas soluciones son estables y robustas? El análisis matemático formal de estas soluciones a partir de los diagramas cordales factibles no garantiza la estabilidad y robustez de dichas configuraciones. Este es un punto que no se debe olvidar nunca, todas estas soluciones teóricas posibles no son estables. Las soluciones que no son establse no pueden darse en la Naturaleza. El estudio analítico de la estabilidad de las soluciones generales está fuera de lo que permiten nuestro conocimiento actual. Incluso de soluciones con tres solitones en interacción es muy difícil. Por ello, lo habitual, como hace Kodama en su artículo de revisión, se recurre a presentar simulaciones numéricas que confirman la estabilidad y robustez. Kodama nos presenta este estudio sólo para alguna de las soluciones patrón que ha obtenido.
Las soluciones estables con múltiples solitones líneas en interacción se han observado en la Naturaleza (como muestran las fotos de Mark Ablowitz que abren esta entrada), sin embargo, la utilidad real de un modelo matemático se demuestra cuando se replican estas observaciones experimentalmente en un laboratorio. Mi interés personal en el año 2000 por las matrices de líneas de transmisión no lineales llevaba implícito el hecho de que realizar medidas eléctricas en un circuito es mucho más fácil que medir ondas en la superficie, pongamos, de un tanque de agua. Yo pensaba que podría reproducir y estudiar las interacciones de múltiples solitones línea con facilidad. Al final, mi proyecto de investigación se quedó en eso, en un proyecto. Sin financiación la investigación es difícil y al final me quedé con lo fácil, unas simulaciones numéricas por ordenador que siempre dejan el mal sabor de boca de ¿y si en la Naturaleza no se observa lo que uno simula en el ordenador?
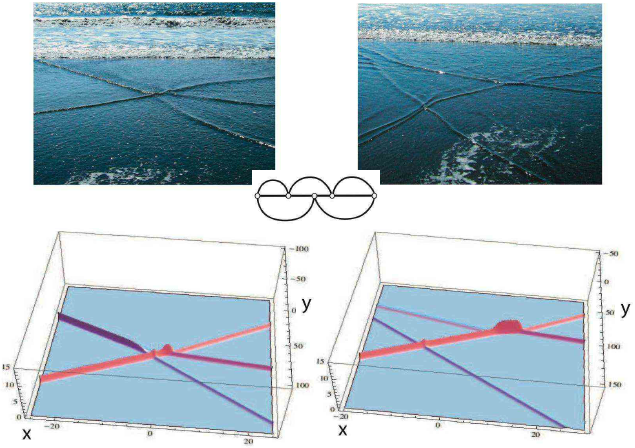
Por ello, me ha dejado un buen sabor de boca el artículo de Kodama que acaba mencionando su trabajo reciente en colaboración con un físico experimental, Harry Yeh (en concreto, Harry Yeh, Wenwen Li, Yuji Kodama, «Mach reflection and KP solitons in shallow water,» ArXiv, 2 Apr 2010). Utilizando una nueva técnica para la medida de las ondas en la superficie de un tanque de agua mediante un láser, llamada fluorescencia inducida por láser (LIF), han logrado reproducir experimentalmente las soluciones de la ecuación KP con una precisión alucinante. La figura de abajo muestra un resultado de su trabajo. Las tres figuras de arriba son resultados experimentales y las tres figuras de abajo son resultados numéricos. Los solitones líneas en estas figuras se mueven hacia la izquierda. Aunque los resultados experimentales muestran cierta dispersión, el modelo teórico da cuenta de los mismos con una exactitud sorprendente. ¡Alucinante!

La mayoría de los lectores de este blog pensarán que chochea la Mula Francis con estos desvaríos. ¿Alucinantes? Bueno, es lo que pasa cuando uno habla de temas relacionados con su propio trabajo… por cierto, ya hace unos años que no estudio numéricamente la ecuación KP, ahora me dedico a otras ecuaciones y otros tipos de solitones. La vida da muchas vueltas… y yo he disfrutado mucho con el trabajo de Kodama, a quien sigo admirando no sin cierta devoción.





Y puestos a seguir chocheando, ¿qué aplicaciones trae el perfeccionamiento de la predicción de este tipo de solitones?.
Me ha entrado la curiosidad.
¿Aplicaciones? Buena pregunta. La ecuación KP modela ondas superficiales en aguas someras cuando la tensión superficial domina, es decir, en películas delgadas. Hay muchos sistemas físicos y biológicos que presentan este tipo de películas, pero pocas aplicaciones prácticas tienen en este contexto los solitones línea y sus interacciones. Eso sí, saber que son un modelo adecuado ayuda a entender la física de estos sistemas (la física de una ecuación integrable es mucho más fácil de entender que uno no integrable). La KP también aparece en ciertos modelos de plasmas y en condensados de Bose-Einstein, donde por ahora sólo tiene interés teórico. Finalmente, la KP modela ondas magnetoelásticas en materiales antiferromagnéticos, cierta interacción entre magnones y fonones, que podrían tener aplicaciones en sistemas de almacenamiento magnético de información, aunque actualmente no se utilizan solitones en estos sistemas.
En resumen, ahora mismo la KP no se aplica tecnológicamente para nada, pero hay varias propuestas teóricas de posibles aplicaciones prácticas para el futuro. No hay que olvidar que los matemáticos aplicados tenemos que vender nuestro trabajo como que sirve para algo, pero son los ingenieros los que tienen que utilizar nuestro trabajo en aplicaciones prácticas.