La violación de la simetría CPT es tan improbable que parece imposible. Pero si el neutrino y el antineutrino tienen masas diferentes la simetría CPT se violaría. Solo gracias a los experimentos se puede saber si el neutrino y el antineutrino son la misma partícula (tipo Majorana) o diferentes (tipo Dirac) y, en este último caso, si tienen la misma masa o diferente. La violación de la simetría CPT sería aún más importante que la violación de la simetría P o de la paridad. Hoy la vemos como algo «normal» en la fuerza débil pero en su momento fue tan revolucionaria como el descubrimiento de la antimateria. Hasta el genial Martin Gardner escribió un libro sobre ella, titulado «Izquierda y Derecha en el Cosmos.» El físico I. S. Tsukerman nos resume en un interesante artículo todo lo que sabe sobre la violación de la simetría CPT y la física de los neutrinos («CPT invariance and neutrino physics,» ArXiv, 24 Jun 2010).
Esta entrada es mi segunda contribución al XI Carnaval de la Física organizado por Germán Fernández, autor del blog El neutrino. Hace ya bastantes años, cuando se descubrió que el neutrino tenía masa, impartí una conferencia divulgativa sobe el descubrimiento y desde entonces algunos amigos me pusieron el «mote cariñoso» de «el neutrino.» Tras la charla la gran pregunta de muchos de ellos era ¿qué es un neutrino? Ellos no sabían qué es un electrón y descubrir que el protón era una partícula elemental «compuesta» les resultó muy chocante. Más chocante fue saber que ni «el neutrino» sabía qué es un neutrino. Sigo sin saberlo. Sigo sin saber qué es una partícula elemental. Por cierto, sobre las propiedades del neutrino hay muchas fuentes, por ejemplo, Carlo Giunti, Alexander Studenikin, «Neutrino electromagnetic properties,» Phys. Atom. Nucl. 72: 2089-2125, 2009 [ArXiv, 18 Dec 2008]
El neutrino es una partícula elemental fascinante, objeto de intensas investigaciones tanto experimentales como teóricas. El neutrino nació en el intento de W. Pauli en 1930 de explicar el espectro continuo de energía en la desintegración nuclear tipo beta, con objeto de salvar la ley de conservación de la energía. Hoy en día, cualquier nueva partícula se descubre gracias a la misma idea. El neutrino es parte fundamental de la teoría de las interacciones débiles de E. Fermi (1934), de la no conservación de la paridad de T.D. Lee y C.N. Yang (1956), del modelo V−A para interacciones débiles locales de R. Feynman y M. Gell-Mann (1958) y, por supuesto, de la teoría electrodébil de Glashow-Weinberg-Salam en el modelo estándar de la física de las partículas elementales. ¿Qué sabemos sobre los neutrinos? Mucho, muchísimo, demasiado para poder resumirlo todo en esta entrada. Pero quizás sea más interesante conocer ¿qué es lo que no sabemos sobre los neutrinos?
En la teoría de Glashow, Weinberg y Salam de los 1960, los neutrinos no tenían masa debido a que la evidencia experimental proponía como límite superior para su masa más de 6 órdenes de magnitud por debajo de la masa del electrón. Un neutrino sin masa era la opción más simple para su teoría. Pero en 1998, el experimento japonés Super-Kamiokande descubrió la primera evidencia de que los neutrinos tienen masa. Dicha evidencia ha sido ratificado por muchos otros experimentos en la última docena de años. Hay tres tipos de neutrinos (pues se conocen tres familias o «sabores» de partículas elementales) llamados electrónico, νe, muónico, νμ, y tauónico, ντ. Si los neutrinos tienen masa no nula pueden cambiar de identidad, pueden cambiar de «sabor» ya que las funciones de onda cuánticas observables de los tres neutrinos, sean me, mμ y mτ, son una mezcla (combinación lineal) de tres funciones de onda con masa no observables, sean m1, m2 y m3. O al revés, ya que la matriz que mezcla los sabores es invertible. La figura de arriba muestra por ejemplo que el estado m1 es una combinación de los tres estados observables (colores rojo, verde y azul). La oscilación de (la identidad de) los neutrinos nos permite calcular la diferencia entre sus masas pero no su valor absoluto. En la actualidad hay dos opciones posibles, mostradas en la figura de arriba. El estado masivo m3 puede tener una masa inferior al estado m1 o superior al estado m2. Solo los experimentos podrán decidir cuál es la opción correcta: si los estados masivos de los neutrinos están ordenados de forma normal o invertida (también habrá que determinar los valores de los coeficientes de la matriz de masas de los neutrinos).
La teoría matemática para el neutrino en el modelo estándar extendido (con neutrinos masivos) permite dos opciones posibles. Como el neutrino es una partícula neutra, podría ser idéntico a su antipartícula (teoría de Majorana) o diferente a ella (teoría de Dirac). La manera más sencilla de distinguir estas dos posibilidades es gracias a la desintegración beta doble sin neutrinos. En la desintegración beta doble un átomo radioactivo se desintegra en un átomo dos unidades de carga menor emitiendo dos electrones. Si el neutrino es una partícula de Dirac es obligatorio que esta desintegración venga acompaña de la emisión de dos antineutrinos (electrónicos). Sin embargo, si el neutrino es una partícula de Majorana y el antineutrino y el neutrino son la misma partícula, podría ocurrir esta desintegración sin emisión de ningún neutrino. Este tipo de desintegración es muy rara y aunque hay varios experimentos en curso estudiando este asunto, todavía no se sabe si el neutrino es igual a su antipartícula.
La simetría CPT es una simetría muy general de casi cualquier teoría cuántica de campos invariante Lorentz (compatible con la relatividad especial) en la que los campos y los conmutadores de los campos son invariantes Lorentz. El teorema suele estar asociado a Pauli, Lüders y Schwinger. La conjugación de carga C corresponde a la invarianza de la teoría cuando se cambian partículas por antipartículas. La paridad P corresponde a la invarianza cuando se reflejan las coordenadas espaciales en un espejo y la invarianza temporal T es cuando se cambia la dirección de la flecha del tiempo. Si una teoría cuántica de campos es invariante CPT entonces automáticamente la masa de las partículas es idéntica a la masa de las antipartículas. Hay que recordar que una teoría que no sea invariante CPT no significa que no sea invariante Lorentz, podría ocurrir que los campos fueran invariantes Lorentz, pero los conmutadores de los campos no lo fueran, es decir, que habría violaciones de la causalidad cuánticas, aunque podría ocurrir que no fueran observables gracias al principio de incertidumbre.
Si el neutrino fuera una partícula de Dirac y la antipartícula del neutrino tuviera una masa diferente (aunque podría ser muy parecida) a del neutrino, la física de los neutrinos violaría la invarianza CPT. Si el neutrino fuera una partícula de Majorana es más complicado (pero posible) incorporar una violación de la simetría CPT (aunque por lo que dice Tsurkerman me parece menos razonable este caso). ¿Qué límites experimentales existen sobre la violación de la simetría CPT en la teoría electrodébil? El límite más restrictivo es la diferencia de masas entre el kaón neutrino y su antipartícula
que se estima en 18 órdenes de magnitud (en unidades relativas). Sin embargo, Tsukerman argumenta en su artículo que este dato podría estar mal interpretado, ya que alude a la violación de la simetría CPT par, pero en el caso de violación CPT impar, el límite actual no supera los 4 órdenes de magnitud. Ahí es donde Tsukerman cree que se puede esconder la violación CPT en la física de los neutrinos, que podría haber escapado a detección hasta el momento. En el sector leptónico, la diferencia de masas entre el electrón y el positrón se estima en al menos 12 órdenes de magnitud relativos.
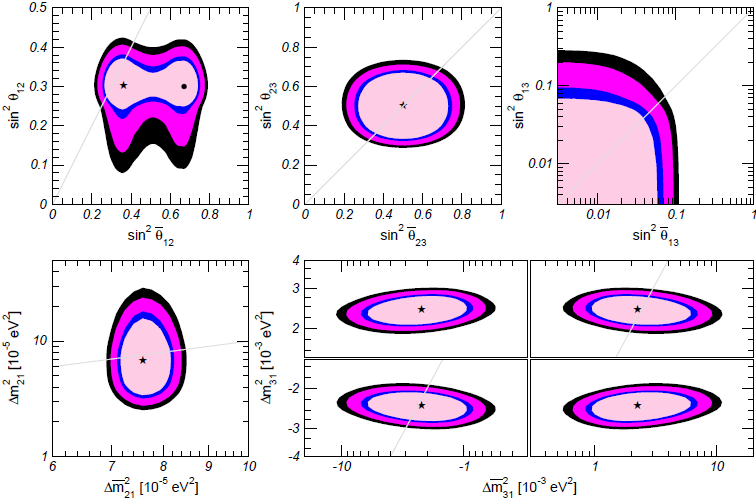
Los experimentos que estudian en detalle la oscilación de los neutrinos han sido capaces de poner límites a la posible violación de la simetría CPT en los neutrinos. Por ejemplo, se sabe que las diferencias de masas entre el neutrino y el antineutrino cumplen que |Δm3| < 1’9 × 10–4 eV y que 7’5 × 10–3 < Δ(mν)² < 5’5 × 10–3 eV. Los mejores límites actuales sobre la posible violación de la simetría CPT en el sector de los neutrinos, es decir, la posibilidad de que la masa del neutrino y del antineutrino sean diferentes nos los resume la siguiente figura (extraída del artículo de M.C. Gonzalez-Garcia, Michele Maltoni, «Phenomenology with Massive Neutrinos,» Phys. Rep. 460: 1-129, 2008 [gratis en ArXiv]). En la figura los contornos corresponden a a las regiones permitidas al 90%, 95%, 99% y 3σ C.L. En esta figura se ha supuesto que el orden de los estados de masa de los neutrinos y los antineutrinos es el mismo (u orden normal u orden invertido). Caso de que el orden fuera diferente entre ambos, los límites serían mucho peores. Estas figuras nos indican que nuestro conocimiento experimental actual permite cierta violación de la simetría CPT compatible con todo nuestro conocmiento sobre la física de los neutrinos.
El artículo de Tsukerman discute diferentes experimentos que se pueden realizar para verificar o no varios tipos de violación de la simetría CPT en la física de los neutrinos. Un artículo de 62 páginas con 330 referencias que nos recuerda que incluso las simetrías sacrosanto de la física de partículas elementales (como en su momento fue la simetría de paridad) han de ser continuamente verificadas ya que en ellas se podría ocultar física más allá del modelo estándar de gran interés.




Excelente artículo, modelo que deberían copiar otras publicaciones de divulgación científica. Saludos:
Alejandro Álvarez
Hola Francis,
me gustó mucho tu artículo, incluye muchos detalles de gran importancia. La idea de que CPT pueda no ser una simetría exacta es tan interesante como la describes que es un área de investigación muy activa experimentalmente así como sus desarrollos teóricos formales.
Me gustaría comentar algunas cosas con respecto a este tema. Cuando se habla de CPT es imposible dejar de mencionar el límite de diferencia de masas de los kaones neutros, sin embargo hay un detalle con este valor y con todos lo que aparecen en la p. 19 de la tabla de CPT invariance del PDG. El asunto es que como bien dices, el teorema CPT implica que la masa de una partícula debe ser igual a la masa de su antipartícula. Sin embargo, la implicancia es sólo en un sentido. Se suele decir que «si se viola CPT entonces la masa de una partícula no es igual a la de su antipartícula», lo que corresponde a un uso de la implicancia del teorema en el otro sentido, lo cual no es necesariamente correcto. En 2002, Oscar Greenberg mostró lo que a veces le llaman «anti-CPT theorem», en cual demuestra que cualquier violación de CPT en teoría de campos implica violación de la simetría de Lorentz [1]. En el mismo paper, Greenberg estudia los efectos de una teoría de campos en la cual las masas de partículas y antipartículas no son iguales, lo que lleva a no localidades que se traducirían en pérdidas de causalidad (como nos cuentas en tu artículos) pero también otras cosas que no queremos que ocurran en una teoría, como secciones eficaces de scattering que dependen del sistema de referencia. Por ello, en el contexto de teoría de campos, las partículas y sus antipartícula DEBEN tener la misma masa (y vida media). Qué significa esto para las mediciones reportadas en la tabla del PDG? No se trata de decir que esos resultados estén mal, sólo significa que esas cantidades no tienen absoluta relación con CPT. Cómo se puede estudiar violación de CPT? Dado el resultado demostrado por Greenberg, se requiere un formalismo que además incluya violación de Lorentz para ser consistente. Dicho formalismo existe desde 1997 y se conoce como Standard-Model Extension (SME), el cual describe en forma general cualquier violación a la simetría de Lorentz con y sin violación de CPT en el modelo estándar [2,3]. Gravedad también fue incluída en este formalismo más tarde (2004), sin embargo el nombre SME se ha preservado [4]. El SME es hoy en día usado en todo el mundo para buscar posibles desviaciones de la simetría de Lorentz. Dichas búsquedas incluyen neutrinos, mesones neutros (K,D,B), relojes atómicos, mediciones astrofísicas, lasers, masers, … la lista es muy larga y todos los resultados de dichos experimentos son recopilados en las «Data Tables for Lorentz and CPT Violation» [5], las que son actualizadas todos los años. En dichas tablas y las respectivas búsquedas no se menciona la diferencia de masas de partículas y antipartículas porque, de acuerdo al teorema de Greenberg, deben ser las mismas. En dichas tablas pueden encontrarse varios límites experimentales de violaciones a Lorentz y CPT en la teoría electrodébil, incluyendo electrones, fotones, neutrinos y mesones neutros.
En el caso de neutrinos, recientemente el experimento MINOS ha publicado los más sensibles valores en la búsqueda de un tipo particular de efecto (modulaciones siderales) que podría ser producido por estas violaciones [6]. Dado que el mismo experimento MINOS ha reportado la posibilidad de que los parámetros que controlan la oscilación de neutrinos podrían no ser los mismos para antineutrinos, también es necesario decir que si dicha diferencia se verifica (es decir, no es sólo un efecto estadístico) entonces al menos uno de los coeficientes del SME podría ser no nulo y podríamos estar en presencia de la primera evidencia de violación de la invariancia de Lorentz.
Una visión bastante extendida me he encontrado en la Wikipedia. A pesar de que muchos artículos de física tienen errores, los relacionados con el SME están muy buenos.
Sólo quería contarte acerca del SME y de la enorme cantidad de evidencia experimental que hasta ahora es consistente con CPT y Lorentz, sin embargo agregaría que los efectos estudiados hasta ahora cubren sólo una pequeña fracción de los posibles efectos medibles y por ellos hay tantos experimentos buscando estas posibles señales. Incluso cada tres años hay una conferencia donde teóricos y experimentales de todas las áreas se reúnen a discutir sus respectivos resultados, la más reciente fue hace un par de meses (CPT’10).
Abajo incluyo algunas de las referencias más importantes sobre el tema por si te interesa. Leyendo tus artículos he visto que profundizas bastante en los temas que discutes lo que me parece loable. Gracias por traer estos temas tan particulares y específicos a tus lectores que no cabe la duda son muchos.
Saludos cordiales,
Jorge
[1] CPT Violation Implies Violation of Lorentz Invariance, arXiv:hep-ph/0201258
[2] CPT Violation and the Standard Model, arXiv:hep-ph/9703464
[3] Lorentz-Violating Extension of the Standard Model, arXiv:hep-ph/9809521
[4] Gravity, Lorentz Violation, and the Standard Model, arXiv:hep-th/0312310
[5] Data Tables for Lorentz and CPT Violation, arXiv:0801.0287
[6] A Search for Lorentz Invariance and CPT Violation with the MINOS Far Detector, arXiv:1007.2791
Muy interesante la entrada, como suele ser norma en este sitio.
Sin embargo, no entiendo esta parte:
Hay que recordar que una teoría que no sea invariante CPT no significa que no sea invariante Lorentz, podría ocurrir que los campos fueran invariantes Lorentz, pero los conmutadores de los campos no lo fueran, es decir, que habría violaciones de la causalidad cuánticas, aunque podría ocurrir que no fueran observables gracias al principio de incertidumbre.
¿Podría dar más detalles?
Gracias.