
Los solitones son ondas no lineales que mantienen su forma incluso en interacciones mutuas (cuando dos de ellos chocan entre sí recuperan su forma inicial tras el choque). En Europa, la conferencia más importante sobre solitones se celebra cada cuatro años en Sevilla. Esta semana, del 9 al 12 de julio, se está celebrando el LENCOS’12 (2nd Conference on Localized Excitations in Nonlinear Complex Systems). Este año de crisis hay 70 charlas y 17 posters sobre temas tan interesantes como solitones en condensados de Bose-Einstein y en cristales fotónicos, breathers en sólidos cristalinos, líneas de transmisión eléctrica y medios granulares, solitones (breathers) en ADN y su relación con procesos cancerígenos, condensados de Bose-Einstein de polaritones, «rogue waves» en plasmas, solitones en metamateriales de grafeno o, incluso, solitones en las ecuaciones no lineales del mecanismo de Higgs y su relación con lo masa del bosón. El programa es realmente interesante, como muestra el libro de resúmenes en pdf.


Sergej Flach (Max Plack-Institut für Physik complexer Systeme, Dresden, Germany) ha iniciado la mañana de hoy hablando de nuevas transiciones de fase en metales que presentan dos estados de tipo solitón en interacción. Un tema de gran interés en el estudio de átomos ultrafríos en redes ópticas, que muestra que las transiciones metal-aislante pueden ser mucho más complicadas de lo que la teoría de perturbaciones nos muestra (las técnicas matemáticas usadas por Flach y su grupo son técnicas no perturbativas). Más información, de nuevo solo para los más osados, en Sergej Flach et al., «Correlated metallic two-particle bound states in quasiperiodic chains,» EPL, 98 (2012) 66002 [offprint gratis].
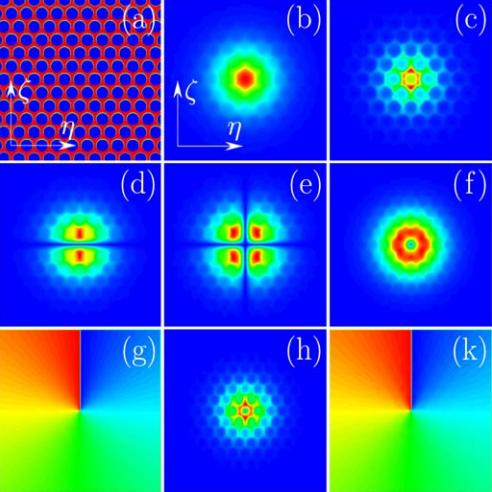
Boris A. Malomed (University of Tel-Aviv, Israel) nos hablará mañana de sus trabajos más recientes junto a Yaroslav V. Kartashov y Lluis Torner (Instituto de Ciencias Fotónicas (ICFO), Barcelona), en los que estudia el efecto que tiene una no linealidad en un sistema óptico que no es homogénea, cambia en el espacio. Hace unos años parecía inconcebible que este tipo de sistemas ópticos se pudieran fabricar, pero gracias a tecnologías recientes, como las fibras de cristales fotónico no lineales, se ha abierto un nuevo campo para el control espacial de los solitones, permitiendo su transmutación de un tipo a otro y posibilitando un amplio abanico de futuras aplicaciones prácticas en sistemas completamente ópticos. Como antes, los más osados disfrutarán de Valery E. Lobanov et al., «Stable bright and vortex solitons in photonic crystal fibers with inhomogeneous defocusing nonlinearity,» Optics Letters 37, 1799 (2012) [arxiv preprint].

La conferencia inaugural fue a cargo de Michael Manley (Lawrence Livermore National Laboratory, USA) que mostró la cara experimental de los solitones (modos intrínsicamente localizados) en sólidos cristalinos. Más información en su revisión M. E. Manley, «Impact of intrinsic localized modes of atomic motion on materials properties,» Acta Materialia 58 (2010) 2926-2935 [arxiv preprint].

Esta tarde nos hablará otro famoso experimental, Alberto Amo (Laboratoire de Photonique et de Nanostructures, CNRS, Marcoussis, France), experto en polaritones, gracias a los cuales ha publicado en Nature y Science. Su trabajo ha permitido observar monopolos magnéticos usando fluidos cuánticos de polaritones (en cierto tipo de condensados de Bose-Einstein). Ciertos solitones se pueden dividir en dos «medio-solitones» (half-solitons) que se comportan como monopolos; parece increíble que hayan podido medir el campo magnético que producen el fluido cuántico. Los interesados en saber más pueden consultar R. Hivet et al., «Half-solitons in a polariton quantum fluid behave like magnetic monopoles,» arXiv:1204.3564, Submitted on 16 Apr 2012.
No puedo comentar muchas más charlas porque alargaría en exceso esta entrada, pero no puedo acabar sin destacar el gran éxito que está siendo LENCOS’12 y la gran labor que han realizado sus organizadores para traer a Andalucía a la crème de la crème de la teoría de solitones. Enhorabuena.


Hola Fancis, ¿No decías que en este blog no ibas a escribir sobre temas a los que te dedicas profesionalmente? Bueno ya que estamos y sin tener ni idea sobre la materia, ¿Se pueden usar los experimentos como guía para encontrar soluciones exactas a las ecuaciones no lineales? Es decir, como un método heurístico que guíe en la obtención de la solución. O por el contrario, la solución se investiga en teoría y luego si se puede se hace el experimento.
El Cid, las dos opciones se han dado en la historia pasada y supongo que se seguirán dando.
Hay múltiples problemas en los que las soluciones experimentales guían la búsqueda de las soluciones analíticas e incluso el desarrollo de nuevos modelos. Pero también hay muchas ocasiones en las que una solución analítica es buscada con ahínco por muchos grupos de investigadores experimentales.
Te pongo un ejemplo. Se sabe que algunas cadenas de ADN conducen la electricidad y otras no. Hay varios modelos teóricos, pero todavía nadie ha encontrado una solución que explique todos los resultados experimentales. Quizás es que todavía no se ha descubierto el modelo teórico correcto, aunque algunos expertos creen que lo falta es encontrar la solución correcta de los modelos de hopping ya existentes (la mayoría solo se pueden resolver numéricamente y no hay «buenas» soluciones analíticas que expliquen los experimentos).
La opinión más común es que una solución estable que sea robusta puede ser descubierta en los experimentos. El problema es que hay varias definiciones de robustez y no siempre es fácil estar seguro si una solución que los teóricos proclaman como robusta en realidad lo es (y será encontrada por los experimentales).
Me interesa mucho esto de los solitones. Podrías decirme un libro ( si es posible en español ) o alguna dirección de internet o algo con lo que pueda profundizar más. Gracias
Ces, hay pocas fuentes en español; te recomendaría «Solitones ópticos» y más breve «Solitones ópticos.» En inglés hay muchas fuentes y muchos libros cuyo título es «Solitons» u «Optical solitons.»